Today's Topic
\(a>0,a\neq1,M>0,N>0\)のとき
- \(\log_a MN = \log_a M + \log_a N\)
- \(\log_a\frac{M}{N} = \log_a M - \log_a N\)
- \(\log_a M^r = r\cdot \log_a M\)
が成り立ち、この公式は定義から求めにくい対数を考える場合に用いれば良い。



この記事を読むと、この問題が解ける!
- $$\log_3 \frac{36}{25}$$
- $$\log_{\sqrt{3}} 168$$

対数の計算方法は指数法則を思い出そう!
ではそんな対数の計算方法を見ていきましょう。
大丈夫、指数の計算法則と見比べながら勉強すると、全く難しくないです。
対数の公式一覧
\(a>0,a\neq1,M>0,N>0\)のとき
- \(\log_a MN = \log_a M + \log_a N\)
- \(\log_a\frac{M}{N} = \log_a M - \log_a N\)
- \(\log_a M^r = r\cdot \log_a M\)

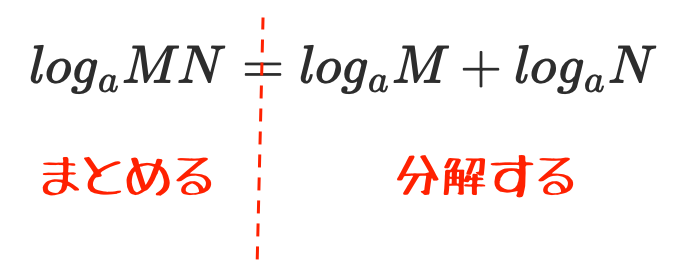
対数の足し算
ポイント
$$\log_a MN = \log_a M + \log_a N$$
一般的な証明は次の通りです。
証明
\(\log_a M = p, \log_a N = q\)とする。
つまり\(M=a^p,N=a^q\)となり、指数法則から\(MN=a^{p+q}\)。
よって、\(\log_a {MN}= p+q=\log_a M+\log_a N\)。
これは指数法則を見ると、より納得できると思います。

この式の指数に着目した式が、まさにこの対数の加法に他なりません。
\(M=a^p,N=a^q\)としてみると、\(MN=a^{p+q}\)となり、\(MN\)は\(a\)の\(p+q\)乗であることがわかります。
\(\log_a {MN}\)を訳すると「\(MN\)は\(a\)の何乗?」となり、これは\(p+q\)乗に他なりませんので
が得られます。
\(\log_a M = p, \log_a N = q\)なので、\(p+q = \log_a M + \log_a N\)と表現しなおせます。
よって、
となるわけですね。
底が同じ対数同士の足し算は、真数同士をかければ良い。
対数の引き算
ポイント
$$\log_a MN = \log_a M + \log_a N$$
対数の足し算と指数法則を理解してれば、全く難しくありません。
証明
\(\log_a M = p, \log_a N = q\)とする。
つまり\(M=a^p,N=a^q\)となり、指数法則から
\begin{align} \frac{M}{N} &= MN^{-1}\\\ &= a^p \times \left(a^q\right)^{-1}\\\ &= a^p\times a^{-q} \\\ &= a^{p+ (-q)}\\\ \end{align}
よって、\(\log_a {\frac{M}{N}}= p-q\)。
\(\log_a M = p, \log_a N = q\)であることから、\(\log_a {\frac{M}{N}}= \log_a M-\log_a N\)。
この式でのポイントは、\(\frac{1}{a}=a^{-1}\)と表せるということです。
つまり\(\frac{M}{N}=M\times N^{-1}\)とすることで、対数の足し算まで帰着できます。

底が同じ対数同士の引き算は、真数同士の分数を考えれば良い。
累乗の対数
最後に、\(\log_a M^r = r\cdot \log_a M\)について考えてみましょう。
証明
\(\log_a M = p\)とする。
つまり\(M=a^p\)となり、指数法則から\(M^r=\left(a^p\right)^r=a^{rp}\)。
よって、\(M\)の\(r\)乗は\(a\)の\(rp\)乗であり、これを数式で表すと\(\log_a {M^r}= r\cdot p\)。
\(\log_a M = p\)であることから、\(\log_a {M^r}= r\cdot \log_a M\)。

指数は対数を取ると、係数として扱うことができる。
対数の計算法則の使い所
対数は多くの学生が苦手とするところですが、その大きな要因の1つがこれら計算公式の乱用です。
定義も考えず、ただ公式に当てはめるだけのパズルゲームにした途端、対数はその魅力を全て失います。
例えば、
例題
$$\log_2 \frac{1}{32}$$
という問題を見たときに、これら計算公式が思いつくようでは全く対数の知識はテストで使い物にならないでしょう。
この程度であれば、




のように計算公式なんか全く使わず、対数の定義から思いつくべきです。
参考【対数の定義】公式で覚えるな!対数とは何か、定義で理解すれば大丈夫!
では、どういった問題で計算法則を使えばいいのでしょう。
それは簡単、「真数って底の何乗?」がものすごく考えにくいときです。
例題
$$\log_3 \frac{81}{32}$$

そうです、こんな不気味な対数になって、ようやく使えばいいんです。
まずは分数が嫌なので対数の引き算に分解します。
81は3の4乗なので\(\log_3 81 = 4\)であることは秒殺です。
ただ32は3の累乗では求まりません。
そこで\(32=2^5\)であることに着目すると、

以上で、
と求められました。
まとめ

まとめ
\(a>0,a\neq1,M>0,N>0\)のとき
- \(\log_a MN = \log_a M + \log_a N\)
- \(\log_a\frac{M}{N} = \log_a M - \log_a N\)
- \(\log_a M^r = r\cdot \log_a M\)
が成り立ち、この公式は定義から求めにくい対数を考える場合に用いれば良い。
今回扱った公式は対数を考える上では基本的な公式となりますが、この公式を使えば良いという問題ではありません。
対数の最も大切なところは、指数の扱いをもっと楽にしたいという思いにあり、別に公式チェック暗記問題ではありません。
是非対数の定義と合わせて、うまく使い分けれるようになってください。
以上、「対数の計算公式について」でした。
チェック問題
例題
$$\log_3 \frac{36}{25}$$


例題
$$\log_{\sqrt{3}} 168$$
168を因数分解すると\(168 = 3\times 2^3 \times 7\)
よって








