【対数関数の定義と性質】グラフからわかる重要性質と問題への使い方を徹底解説！

 

 

 

対数関数の定義

 

 

底の条件・真数条件

この定義だと、指数関数と同様、

の2通りが考えられますが、

の場合は、対数関数として考えないと言っています。

 

このように対数関数には底\(a\)に関する条件と、それに伴って真数\(x\)に関する条件という2つの制約が伴っています。

一般に対数が問題として出題されるときは、この2つの条件を暗黙の了解とする「対数関数」が意図されています。

 

なぜこの条件が必要なのかは、別記事で詳しく解説しますが、この条件を見逃すと高確率で減点を喰らいますのでご注意ください。

参考【底の条件・真数条件】対数関数には、なぜこの2つの条件が必要なのか。→関数じゃなくなるから

 

対数関数の性質・特徴

 

対数関数\(y = \log_a x\)は主に、底\(a\)が\(0< a < 1\)のときと、\(1 < a\)のときの2パターンに分けられます。

 

グラフの形

底\(a\)が\( 1< a\)のとき

次に\( 1< a\)のときですが、グラフの形はこのようになります。

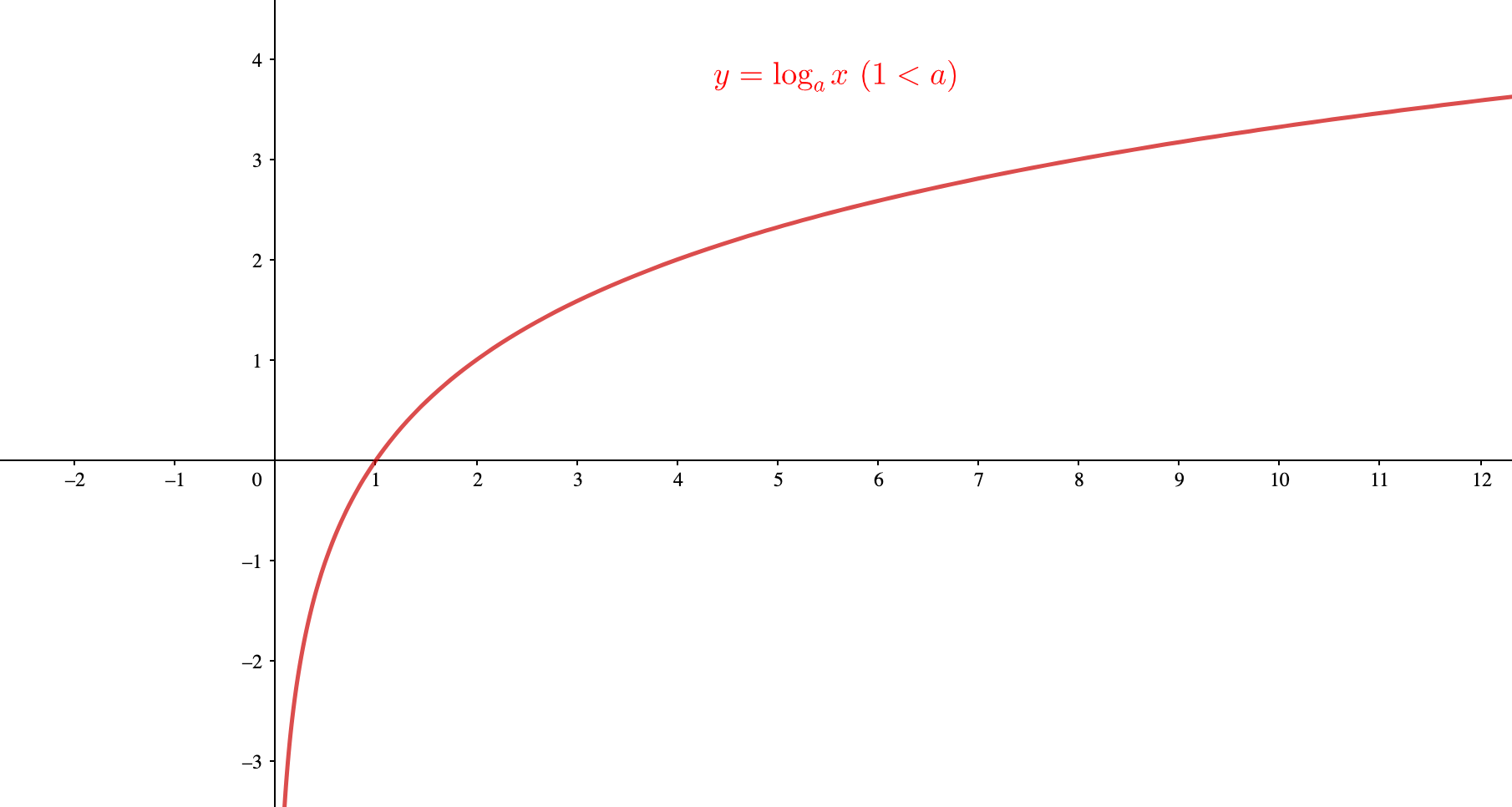
真数条件である\(0<x\)の条件の通り、定義域は0より大きい値しか取りません。

また、\(x\)が大きくなるほど\(y\)の値は緩やかに増加していき、\(x\)の値が0に近づくほど\(y\)の値は無限に小さくなっていきます。

 

底が\(1< a\)の対数関数は\(x\)が大きくなるほど、緩やかに増加していく。

 

底\(a\)が\( 0< a < 1\)のとき

次に\( 0< a < 1\)のときですが、グラフの形はこのようになります。

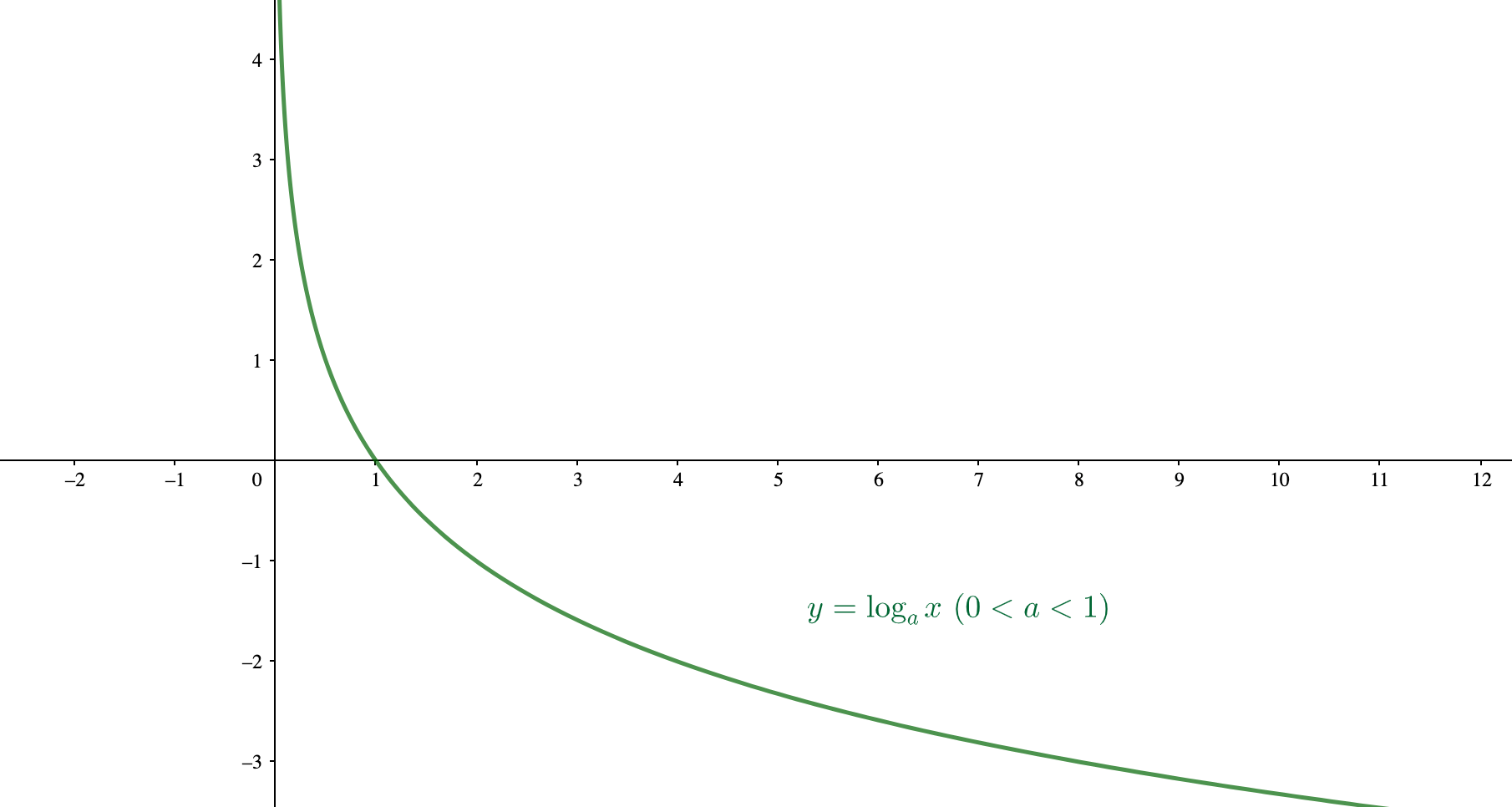
こちらも真数条件である\(0<x\)の条件の通り、定義域は0より大きい値しか取りません。

また、\(x\)が大きくなるほど\(y\)の値は緩やかに減少していき、\(x\)の値が0に近づくほど\(y\)の値は無限に大きくなっていきます。

 

底が\(0< a < 1\)の対数関数は\(x\)が大きくなるほど、緩やかに減少していく。

 

なぜ底の違いでグラフの形が全く異なるのか？

 

と思った方のために、ちょっとだけ詳しくお話ししましょう。

 

対数\(\log_2 8\)は「8は2の何乗？」と訳すことができ、

と

は全く同じことを意味していました。

参考【対数の定義】公式で覚えるな！対数とは何か、定義で理解すれば大丈夫！

 

このとき、2のことを底、8のことを真数、そして3のことを指数というのでした。

 

では、この底が1よりも小さい値、具体例として\(\frac{1}{2}\)のときを考えてみましょう。

対数関数\(y=\log_{\frac{1}{2}} x\)について考えると、「\(x\)は\(\frac{1}{2}\)の\(y\)乗」、つまり\(x = \left(\frac{1}{2}\right)^y\)となります。

指数関数を思い出すと、\(x\)の値が大きくなるためには、\(y\)の値はどんどん小さくなる必要があります。

参考【指数関数のグラフと性質】これだけはサッと思い出したい、超重要な6つの性質

 

よって、\(x\)が大きくなると必然的に\(y\)の値は減少していくのです。

 

これは底が1よりも大きい値のときでも同様です。

具体例として\(y = \log_2 x\)を考えてみると、日本語訳は「\(x\)は2の\(y\)乗」ということになります。

\(x\)が大きくなるためには、2をより多くかけていけばいいわけですから、\(y\)の値は増加していくということになりますね。

 

底が1よりも小さい場合、指数が大きいほど値は小さくなる。そのため底が1よりも小さい対数関数では\(x\)の増加に伴い、\(y\)の値が減少していく。

 

グラフからわかる性質

 

グラフを見てみると、重要な性質を発見することができます。

 

必ず座標\((1, 0)\)を通る

 

底がどのような値でも、グラフを見てみると必ず座標\((1, 0)\)を通っていることがわかります。

これは対数そのものを考えれば当たり前のことです。

 

$$y = \log_a x$$

において、\(x=1\)のとき、指数関数では\(a^y = x = 1\)となるから\(y＝0\)となるのは明らか。

 

\(y=x\)に関して指数関数\(y=a^x\)と線対称

 

この性質も底にかかわらず、対数関数のグラフ\(y=\log_a x\)は指数関数\(y=a^x\)と\(y=x\)に対して線対称です。

これも底\(a\)の値にかかわらず成り立つものですが、実際にグラフを見てみましょう。

 

\(1<a\)のとき

 

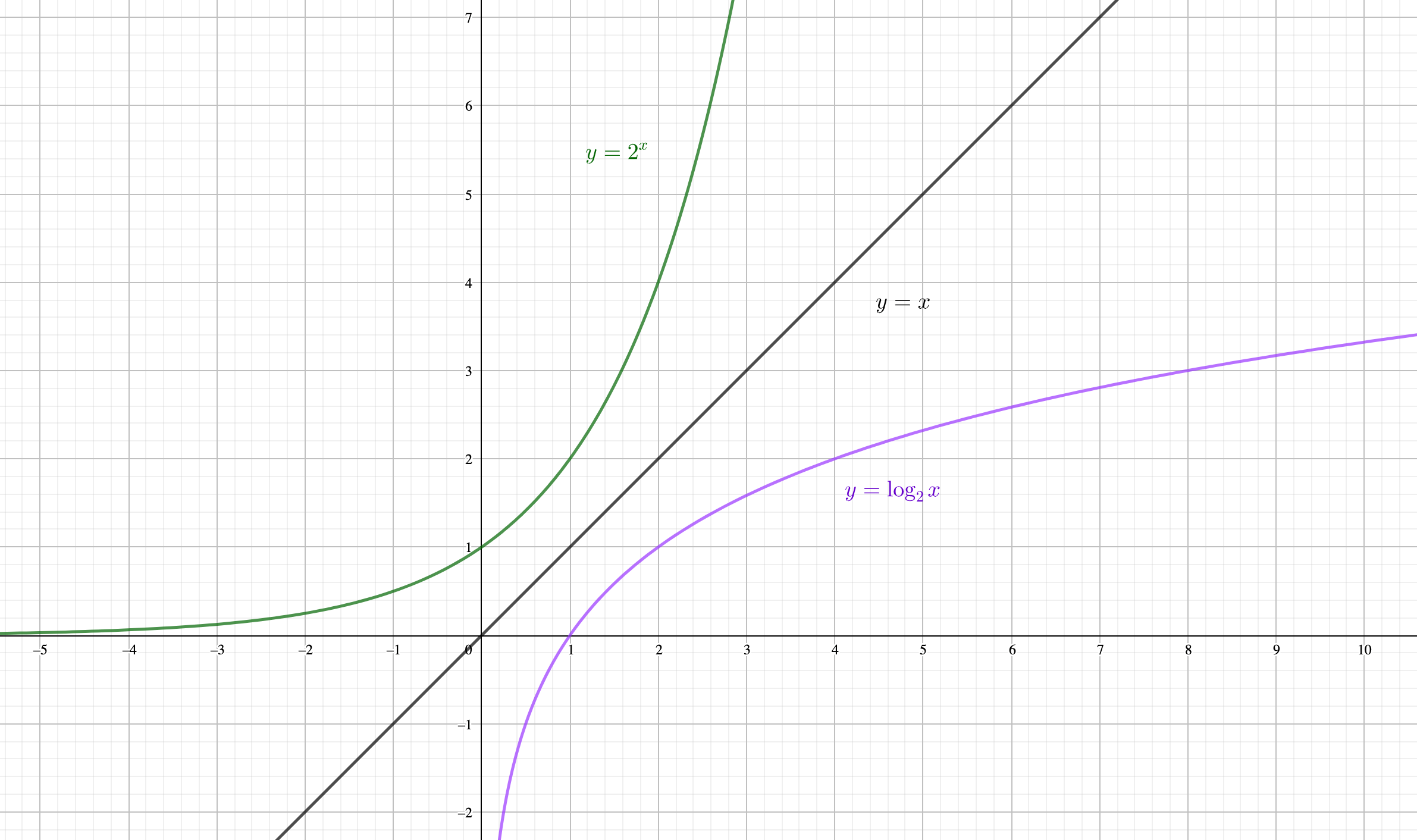
\(0<a<1\)のとき

 

 

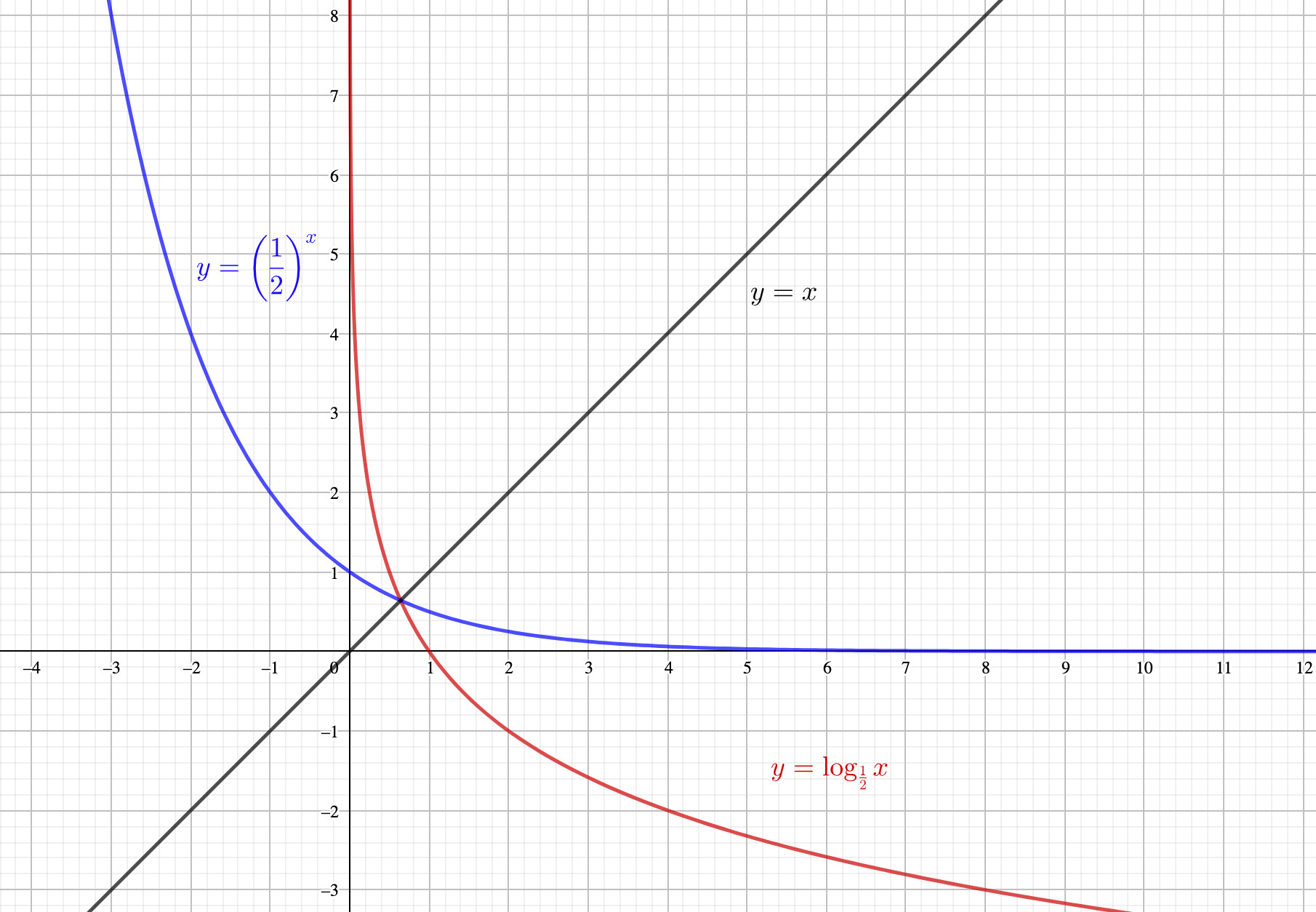
参考【逆関数】グラフから考える『入れ替える』意味と、逆関数の美しい性質

 

\(y\)軸が漸近線

 

底\(a\)の値によらず、対数関数のグラフは\(y\)軸に絶対に触れることはありません。

これは指数関数に直して考えてみると、明らかすぎて涙が出ます。

 

\(y\)軸と触れるということは、すなわち\(x=0\)を通る必要があります。

を日本語訳すると、「0は\(a\)の\(y\)乗」となります。

 

\(a\)が0であればこの条件を満たす\(y\)の値は全ての実数であることがわかりますが、底の条件から残念ながら\(a\)は0になることはありません。

 

よって\(x=0\)になることは決してないので、対数関数のグラフが\(y\)軸と触れることは絶対にないと言い切れるのです。

 

参考【底の条件・真数条件】対数関数には、なぜこの2つの条件が必要なのか。→関数じゃなくなるから

 

単調増加・単調減少するグラフである

 

もう一度、底\(a\)が\( 1< a\)のときのグラフを見てみましょう。

 

\(1<a\)のとき

 

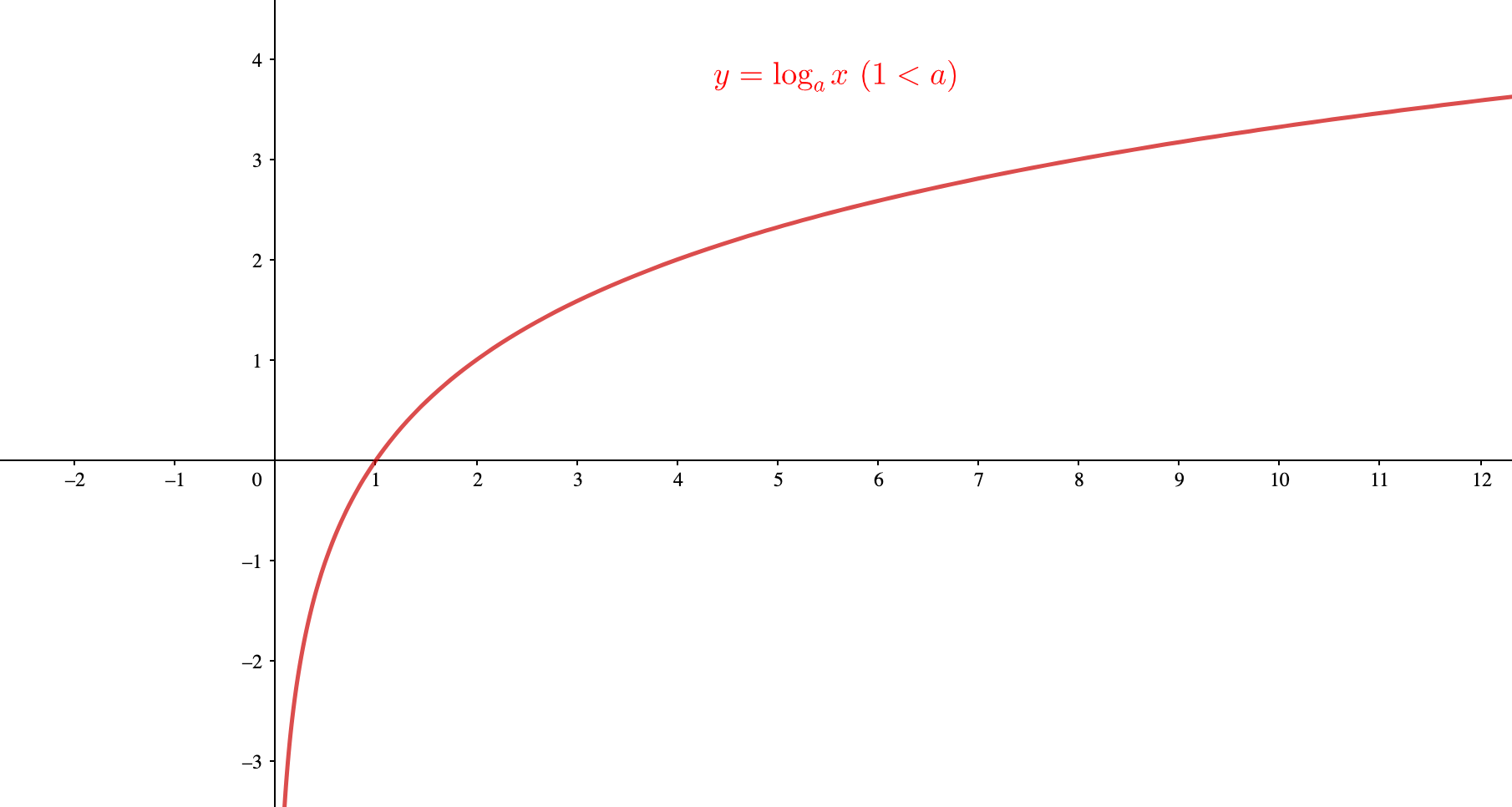
このグラフを見てみると、緩やかではありますが、\(x\)の値が大きくなるほど、\(y\)の値がず〜っと大きくなっていることがわかります。

 

このず〜っと大きくなるというのは、\(p< q\)の条件のもと\(x = p\)と\(x=q\)を考えたとき、必ず\(y=log_ a p\)の値よりも\(y=log_a q\)の値が大きくなっているということです。

 

これを数学では単調増加といいます。

 

底が\( 0< a < 1\)のときも似たような現象が見られます。

\(0<a<1\)のとき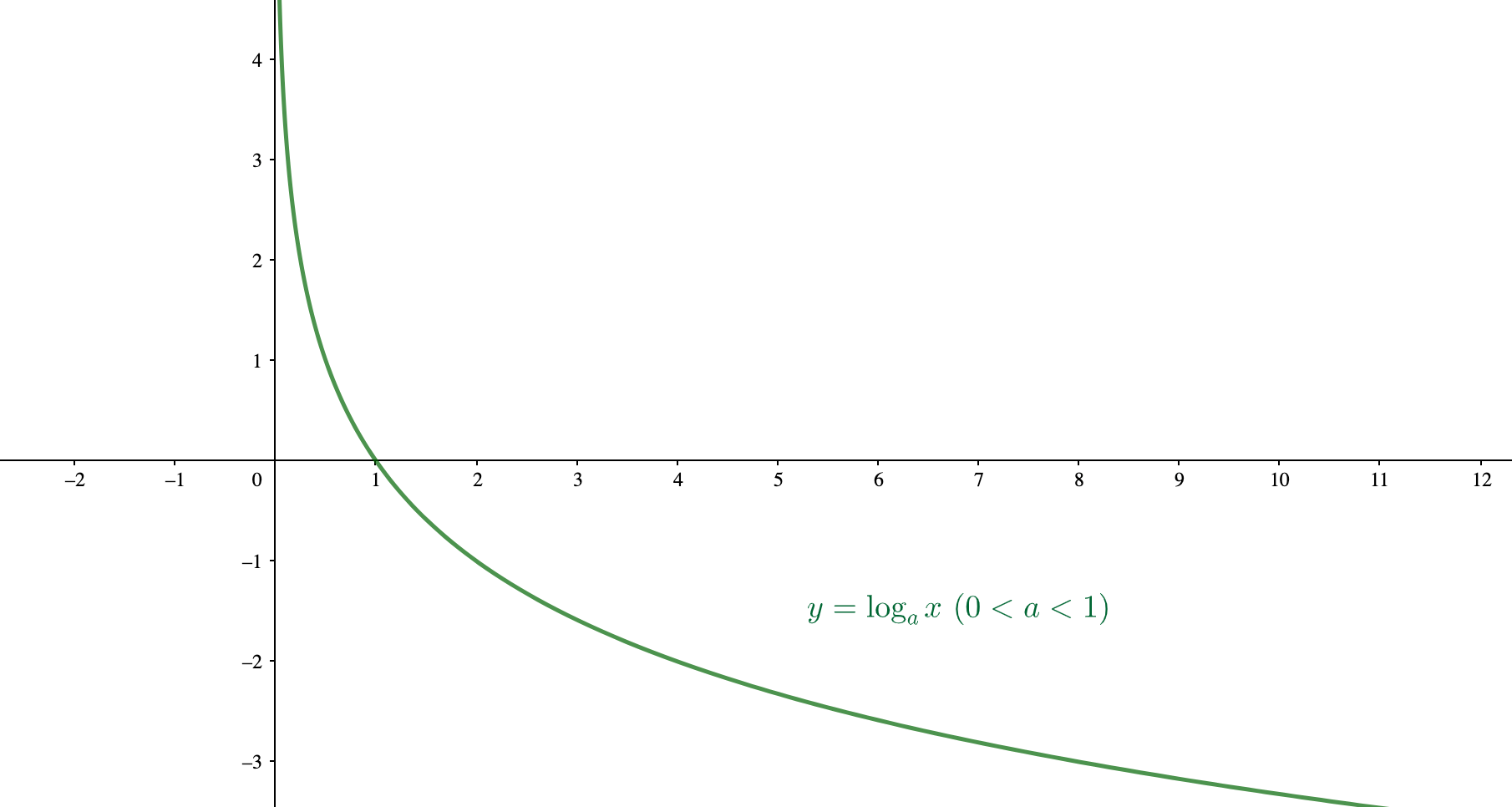

 

こちらは\(x\)の値が大きくなるたびに、\(y\)の値が緩やかではありますが、ず〜っと小さくなり続けています。

これは\(p< q\)の条件のもと\(x = p\)と\(x=q\)を考えたとき、必ず\(y=log_ a p\)の値よりも\(y=log_a q\)の値が小さくなっているということです。

 

これを数学では単調減少と言います。

 

対数関数では次の性質が成り立つ

 

対数関数の例題

 

これをもとに考えると、対数関数を含む方程式や、対数の大小関係が明確にわかるようになります。

対数の大小関係

対数の計算法則を用いると、

となる。

 

対数関数\(y=\log_5 x\)を考えると、底5は1よりも大きいため単調増加することがわかる。

すなわち\(x\)の値が大きいほど\(y\)の値も大きくなるので、\(\log_5 8 < \log_5 9\)となる。

よって、

 

参考【底の変換公式】底を揃える意味や、使える場面を徹底解説！

 

対数関数の不等式

 

 

与式を底が同じ対数で表現すると、\(3 = \log_2 8\)より

 

底2は1よりも大きいので\(y = \log_2 x\)は単調増加する。

よって\(x\)の値が大きいほど\(y = \log_2 x\)の値も大きくなるので、\(x ≦8\)。

 

ここで、真数条件より\(x>0\)。

 

よって共通範囲から

 

 

対数が絡む問題のポイント

 

このように対数の問題には、いろいろバリエーションがありますが最も使われる手法としては

という3つです。

 

対数が現れた場合、この3つを即座に思い出せるようにしておいてください！

 

まとめ

 

 

 

今回は長くなってしまいましたが、対数関数の定義と性質はこれだけです。

今後いろんな対数の問題と出くわすと思いますが、結局対数は指数関数の言い換えでしかないため、それほど難しくできないのが現状です。

 

抑えるべき点はしっかり抑えて、変な公式暗記に頼るよりも、根本的な理解を深めることでどんな場面でどんな手法が使えるのかをじっくり考えていきましょう。

 

以上、「対数関数の定義と性質について」でした。

 

チェック問題

 

 

真数条件より、\((x-8) > 0\)。よって、

 

対数の計算法則より、

 

よって

と考えることができ、これを展開して整理すると

これは\((x-9)(x+1) = 0\)より、\(x=-1, 9\)

 

ただし、真数条件より\(x>8\)であったので、

 

 

 

真数条件より、\(x - 1 > 0\)。

よって、\(x>1\)。

 

与式の底が同じ対数に揃えると、

 

底\(\frac{1}{2}\)は1よりも小さいので、このときの対数関数\(y=\log_{\frac{1}{2}} x\)は単調減少する。

つまり、\(x\)の値が小さいほど\(y=\log_{\frac{1}{2}} x\)の値は大きくなるので、

 

整理すると、\(x < \frac{5}{4}\)となる。

 

ただし、真数条件より\(x>1\)であったので、共通範囲より