Today's Topic
累乗を掛け算として扱いたい場合や、指数を計数として扱いたい場合は、真数条件に注意した上で両辺に適当な底\(n\)を持つ対数をくっつければ良い。





この記事を読むと、この問題が解ける!
- \(2^x = 3^y = \sqrt{6}\)が成り立つとき、$$\frac{1}{x} + \frac{1}{y} $$の値を求めよ。

「両辺に対数をとる」とは
真数条件と同じ、「0よりも大きい」ことが保証されている2つの変数\(a, \ b\)に対して、
という方程式が成り立っていた場合、底\(n\)の対数を両辺にくっつけた
もまた成立し、このように「適当な底を持つ対数を両辺にくっつける」ことを「両辺に対数を取る」といいます。
ただしこのテクニックが使えるのは、最初の等式の\(a=b\)において、どちらの変数も0より大きいという真数条件を満たす場合のみということを忘れないでください!
【証明】なぜ両辺に対数が取れるのか
このテクニックを数学の言葉で表現すると、
両辺に対数をとる
\(a=b>0, n\neq 1, n>0\) であるとき
$$a=b \Leftrightarrow \log_n a = \log_n b$$
となります。
\(\Leftrightarrow\)は同値ということを表し、
かつ
であることを表していましたね。
つまり、この2つをそれぞれ証明していけばいいわけです。
まず①は自明でしょう。

次に②ですが、これには関数の考え方が必要です。
参考【関数とは】中学生でも大丈夫!曖昧にしがちな関数の特徴をしっかりマスターしよう
まずは対数関数について思い出してみましょう。
定義
\(x>0, n\neq1, n>0\)の条件のもと
$$y=\log_n x$$
で定義された\(y\)は\(x\)の関数となっており、これを対数関数と呼ぶ。
つまり、
- \(\log_n a\)は対数関数\(y=\log_n x\)の\(x=a\)のとき
- \(\log_n b\)は対数関数\(y=\log_n x\)の\(x=b\)のとき
とわかります。
そして関数とは、\(x\)が1つ決まれば\(y\)の値が1つに決まる場合を表していました。

ということは、次のことが言えるわけです。
\(a=b\)であるならば、関数の定義上、\(x=b\)のときの\(y=\log_n b\)は\(y=\log_n a\)と一致している以外考えられない。
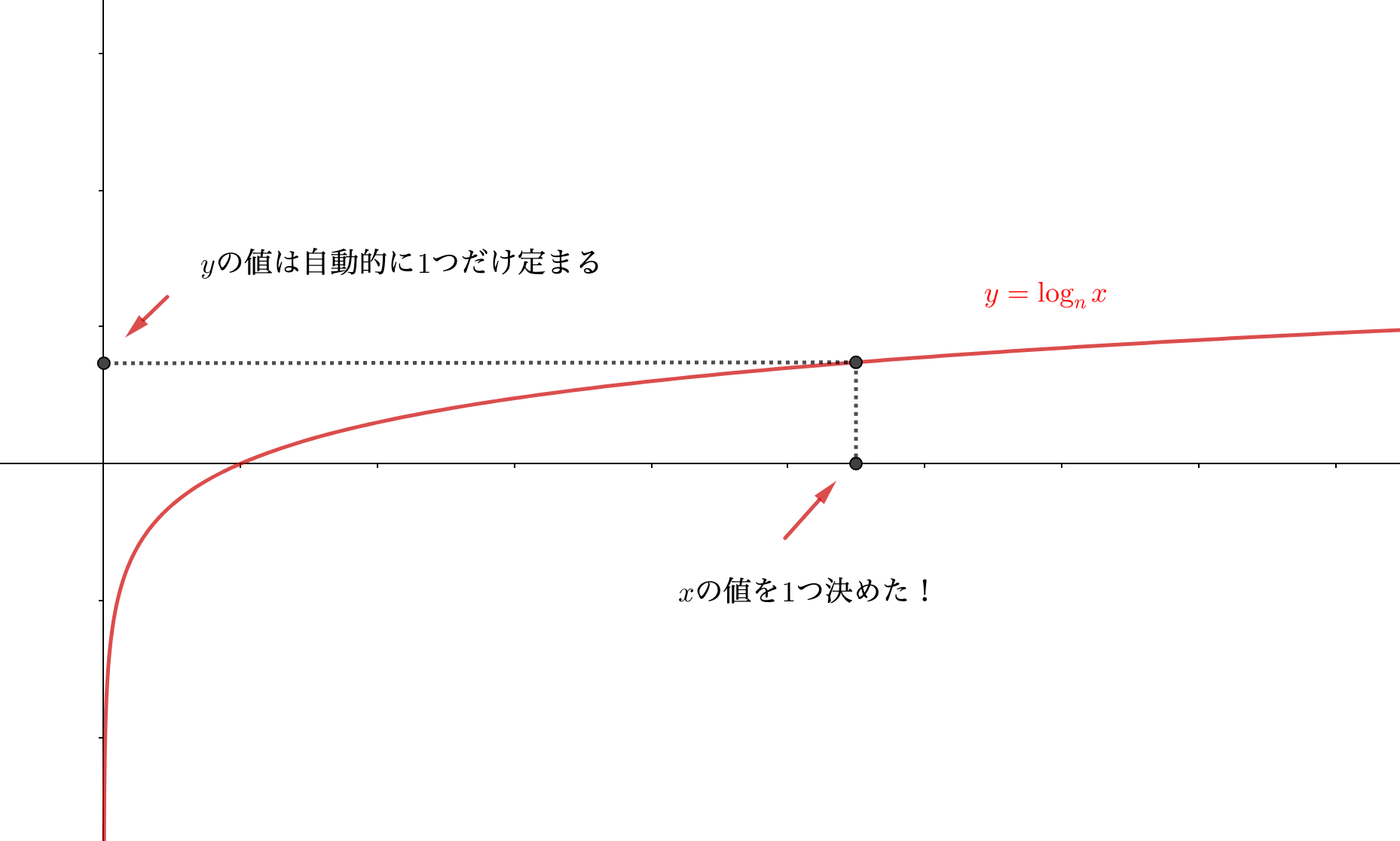
グラフで考えると、図のようにある\(x\)の値を1つ決めると、\(y\)の値は1つに決まるわけだから、指定した\(x\)の値\(a\)と\(b\)が同じだったなら\(y\)の値が一致しないとおかしいよねってことです。
メモ
関数でない場合、\(x=a\)かつ\(a=b\)だからといって\(y\)の値が一致するとは限りません。
例えば円の場合、
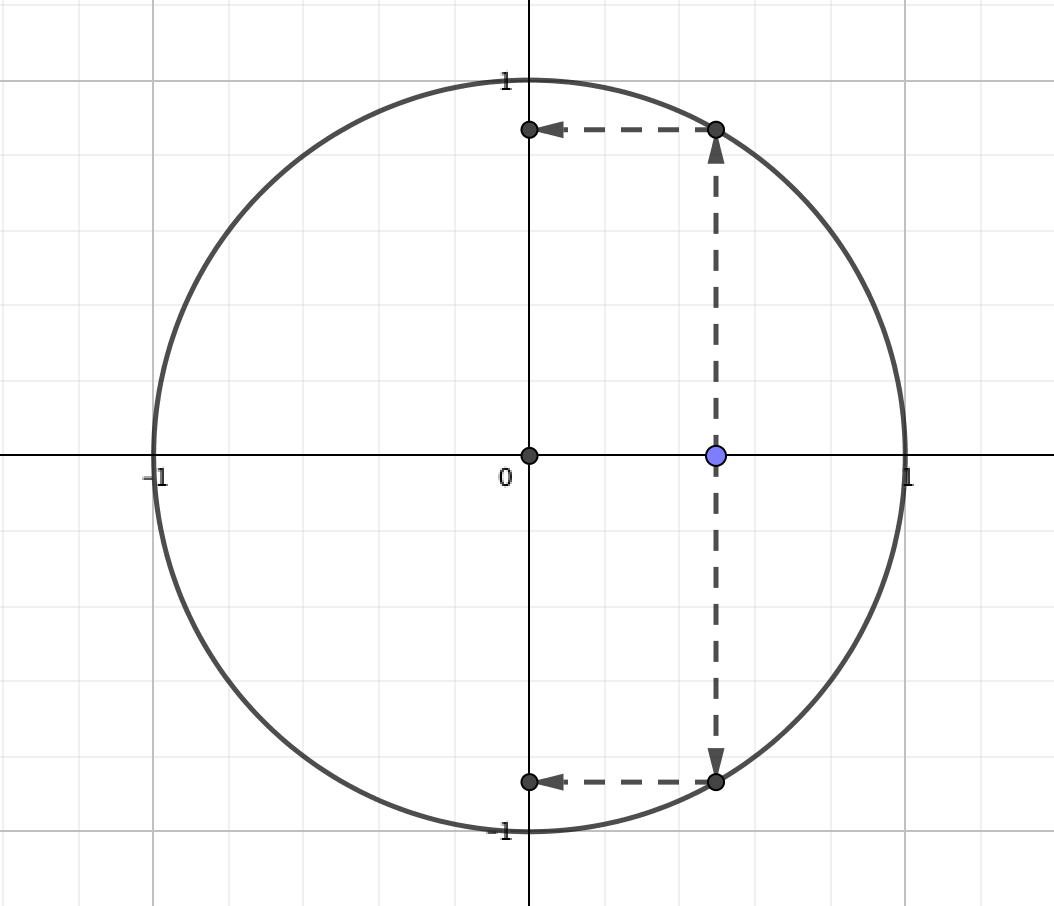
\(x\)の値を1つ決めても、\(y\)の値が2つ定まってしまいます。
つまり②の証明は、対数関数が関数であるからこその証明なんですね!
よって②も成り立つので、①かつ②より「両辺に対数をとる」変形は\(a=b\)が成り立てば絶対に成り立つということがわかりました。
両辺に対数をとるテクニックを使う場面
ではこのテクニックはどんな場面で使えばいいのでしょうか。
結論からいうと、このテクニックは証明や問題解決の中で重要な式変形の1つとして登場することが多いです。
具体例を見てみましょう。
例題
\(a>0,\ b>0,\ n>0,\ a\neq1,\ n\neq1 \)のとき
$$\log_a b = \frac{\log_n b}{\log_n a}$$
を証明せよ。
対数の性質でも登場した
を考えます。
参考【対数の性質】定義を考えれば当たり前。暗記0で理解する対数の必須性質
左辺、右辺共に0より大きいので、両辺に\(n\)を底にもつ対数をとると
となります。
指数を前に下ろすと、
\(\log_n a\)は0でないので、両辺\(\log_n a\)で割ると
となり、与式が証明できた。
このように、対数には指数を扱いやすくする効果があるため、あえて対数を両辺にとることで指数をうまく活用することができました。
ただしこれはあくまで真数条件を満たしている条件の元でしか行えないことを忘れないでください。

参考【底の変換公式】底を揃える意味や、使える場面を徹底解説!
両辺に対数が取れない場面
ちなみに、両辺に対数が取れない場面も見ておきましょう。
例題
$$x^2 =1$$
例えばこの両辺に底が\(n\)の対数をとって見ると、
$$2\log_n x = 1$$
より\(x=1\)となりますね。

はいその通り。
正しい答えは\(x=\pm 1\)ですね。
これは真数となる\(x\)の部分が\(x>0\)であると保証されていないにも関わらず、\(x=-1\)という解答を勝手に無視している悪い例です。
もう一度言いますが、真数条件を満たしている場合にしかこのテクニックは使えません。
まとめ

まとめ
累乗を掛け算として扱いたい場合や、指数を計数として扱いたい場合は、真数条件に注意した上で両辺に適当な底\(n\)を持つ対数をくっつければ良い。
対数は本来指数を扱いやすくするためのものなので、指数が複雑であればあるほどこのテクニックが活きてきます。
証明が出ることはあまりありませんが、だからこそ、曖昧にせずしっかり理解しておくことで対数関数としての利点も明確に理解できるようになりますよ!

以上、「両辺に対数をとるテクニックについて」でした。
チェック問題
例題
\(2^x = 3^y = \sqrt{6}\)が成り立つとき、$$\frac{1}{x} + \frac{1}{y} $$の値を求めよ。
全ての辺に底が6の対数をとると
- \(\log_6 2^x = x\log_6 2\)
- \(\log_6 3^y = y\log_6 3\)
- \(\log_6 \sqrt{6} = \frac{1}{2}\)
となる。
なので、
同様に
なので、
よって








