Today's Topic
\(a>0, a\neq1, M>0\)のとき、
\(\log_a M =p \iff a^p = M\)




この記事を読むと、この問題が解ける!
- $$\log_{36} 16=\frac{2}{1+\log_2 3}$$を示せ。
- $$\log_{81} 27$$を簡単にせよ。
Contents
対数は指数の逆! 何乗かを考えよう!
対数のポイント
\(a>0, a\neq1, M>0\)のとき、
\(\log_a M =p \iff a^p = M\)
まず対数の本質を理解していきましょう。

問1
2の3乗はいくらか。
この問題の答えは簡単、2×2×2=8となりますね。
2の3乗は\(2^3\)のように書くことができ、この表記の3を指数と言います。
ではこの問題はどうでしょうか?
問2
8は2を何乗した数か。
この問題は\(8=2^x\)の\(x\)の値を求めろと言っています。答えは当然、3ですね。
これを数学では\(x=\log_2 8=3\)と表します。
対数は、この問2のような指数\(x\)の値を求める処理を簡略的に書き表したものだと思ってください。
指数計算は同じ数を複数回かけたときの値を求めるのに対して、対数はある値が同じ数を何回かけると作れるか、を考えています。
ポイント
\(\log_2 8\)は「8は2を何乗した数ですか?」と訳せばいい。

ちなみに\(\log_2 8\)の2の位置にある数を底、8の位置にある数を真数といいます。
合わせて覚えておきましょう。
例題
\(\log_{10} 100\) の値を求めよ。
(解答)
100は10の何乗か、と聞かれているだけです。
\(100=10^2\)より、\(\log_{10} 100=2\)
対数の性質
対数は指数の性質を見ることで簡単に理解することができました。
ここでは対数の基本性質を、指数の基本性質を通して見ていきます。
まず指数において、\(a^0=1\)という定義がありました。
これを対数で表すと、次の性質がわかります。
対数の性質⑴
\(\log_a 1 =0 \iff a^0 = 1\)
また、\(a^1=a\)であることから次のこともわかります。
対数の性質⑵
\(\log_a a =1 \iff a^1 = a\)

【超便利】対数の計算方法
ではそんな対数の計算方法を見ていきましょう。
大丈夫、指数の計算法則と見比べながら勉強すると、全く難しくないです。
対数の公式一覧
\(a>0,a\neq1,M>0,N>0\)のとき
- \(\log_a MN = \log_a M + \log_a N\)
- \(\log_a\frac{M}{N} = \log_a M - \log_a N\)
- \(\log_a M^r = r\cdot \log_a M\)

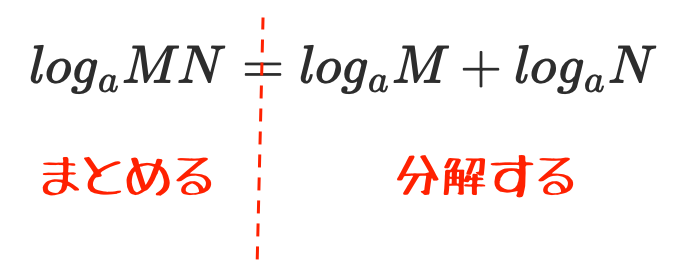
対数の足し算
\(\log_a MN = \log_a M + \log_a N\)となる理由について考えていきましょう。
一般的な証明は次の通りです。
証明
\(\log_a M = p, \log_a N = q\)とする。
つまり\(M=a^p,N=a^q\)となり、指数法則から\(MN=a^{p+q}\)。
よって、\(\log_a {MN}= p+q=\log_a M+\log_a N\)。
これは指数法則を見ると、より納得できると思います。

この式の指数に着目した式が、まさにこの対数の加法に他なりません。
\(M=a^p,N=a^q\)としてみると、\(MN=a^{p+q}\)となり、\(MN\)は\(a\)の\(p+q\)乗であることがわかります。
\(\log_a M = p, \log_a N = q\)であることから、\(\log_a {MN}= p+q=\log_a M+\log_a N\)は納得ですね。
対数の引き算
次に\(\log_a MN = \log_a M + \log_a N\)となる理由について考えていきましょう。
対数の足し算と指数法則を理解してれば、全く難しくありません。
証明
\(\log_a M = p, \log_a N = q\)とする。
つまり\(M=a^p,N=a^q\)となり、指数法則から\(\frac{M}{N}=a^p\times a^{-q}=a^{p-q}\)。
よって、\(\log_a {\frac{M}{N}}= p-q\)。
\(\log_a M = p, \log_a N = q\)であることから、\(\log_a {\frac{M}{N}}= \log_a M-\log_a N\)。
この式でのポイントは、\(\frac{1}{a}=a^{-1}\)と表せるということです。
つまり\(\frac{M}{N}=M\times N^{-1}\)とすることで、対数の足し算まで帰着できます。

累乗の対数
最後に、\(\log_a M^r = r\cdot \log_a M\)について考えてみましょう。
証明
\(\log_a M = p\)とする。
つまり\(M=a^p\)となり、指数法則から\(M^r=\left(a^p\right)^r=a^{rp}\)。
よって、\(M\)の\(r\)乗は\(a\)の\(rp\)乗であり、これを数式で表すと\(\log_a {M^r}= r\cdot p\)。
\(\log_a M = p\)であることから、\(\log_a {M^r}= r\cdot \log_a M\)。

底の条件、真数条件の意味
さて、これまでご紹介した対数の公式には、よく忘れがちな重要ポイントがあります。
それは、式の前に書かれている条件
『\(a>0,a\neq1,M>0,N>0\)のとき』
です。
\(M\)や\(N\)の条件を真数条件といい、\(a\)の条件を底の条件ということがあります。
では、この条件は一体なんのために必要なのでしょうか?
実はこの条件がなくても成り立つ場合があります。
しかし、都合が悪い(というかめんどくさ)ため、このように定義したのです。
理解するために、\(a<0\)のときを考えてみましょう。
そうですね、\(a=-2\)とでもしましょうか。
このとき\(a^3=-8\)となり、これを対数で表すと\(\log_{-2}-8=3\)となります。


では、\(\log_{-2}8\)の値はどうでしょうか。
言い換えるなら\(\left(-2\right)^x=8\)となるような\(x\)が存在するでしょうか。
\(\left(-2\right)^x=\left(-1\right)^x\times \left(2\right)^x=8\)なので、\(x\)が偶数かつ3であれば満たします。

つまり、\(a<0\)をOKとしてしまうと、対数の値が存在したりしなかったりして扱いにくいのです。
数学にはこのように『存在したりしなかったり』な場合がありますが、対数のように便利なものを扱うときは、思い切って考えないようにします。

真数条件も同じです。例えば\(M<0\)もOKだとしてみましょう。
すると、\(\log_2{-8}\)という値(\(2^x=-8\)となるような値\(x\))は存在しませんので、先ほどと同じ議論になります。
練習
底の条件\(a\neq1\)が必要な理由を説明してみよう。
(解説)
\(a=1\)がOKだとする。
\(\log_1 M\)の値、すなわち\(M=1^x\)を満たす値\(x\)について考えてみると、どんな\(x\)の値を取っても\(M=1\)しかありえない。
すなわち、\(M\)が1以外の場合には使い物にならないので、\(a\neq1\)を底の条件としています。

【テストで大活躍】知っておきたい対数の公式
対数の性質が大方わかったら、次にテストで使える対数の公式をマスターして行きましょう。
ただし、これから紹介する対数の公式は全て、底の変換公式から派生しているものです。
まずは底の変換公式をマスターしましょう。
底の変換公式
底の変換公式
\(a,b,c>0\)かつ\(a\neq1,c\neq1\)のとき
\(\log_a b = \frac{\log_c b}{\log_c a}\)
証明
\(\log_a b = p\)とおく。すなわち、\(a^p = b\)。
両辺\(c\)を底とする対数をとると、\(\log_c a^p = \log_c b\)。
対数の公式から\(p\cdot \log_c a = \log_c b\)。
\(a\neq1,c\neq1\)より\(\log_c a\neq0\)。
よって\(p = \frac{lob_c b}{\log_c a}\)なので、\(\log_a b= \frac{lob_c b}{\log_c a}\)となる。

練習
\(\log_{27} 9\)をより簡単に表せ。
(解答)
この対数をそのまま解こうとすると、「9って27の何乗?」に答える必要があり、指数慣れしていないと少しキツイです。
そこで27と9という数に着目してみましょう。
27も9も3の累乗ですよね?

つまり、\(\log_{27} 9\)を底が3の対数に変換してしまえば、簡単に考えることができます。
よって\(\log_{27} 9 = \frac{\log_3 9}{\log_3 27}=\frac{2}{3}\)が得られます。

底と真数の入れ替え
底と真数の入れ替え
\(\log_a b = \frac{1}{\log_b a}\)
証明
実は底の変換公式を使えば全く難しくない。
\(\log_a b=\frac{\log_b b}{\log_b a}=\frac{1}{\log_b a}\)。

底が複雑な対数の簡易化
底が複雑な対数の簡易化
\(\log_{a^p}b = \frac{1}{p} \log_a b\)

証明
これも底の変換公式を使うことで、証明することができる。
\(\log_{a^p}b = \frac{\log_a b}{\log_a a^p} = \frac{\log_a b}{p\cdot \log_a a}=\frac{1}{p}\log_a b\) 。


対数乗
対数乗
\(a^{\log_a x}=x\)


まず\(\log_a x=y\)とすると、\(a^y=x\)とすることができます。
では、\(y\)を\(\log_a x\)に戻してあげましょう。
\(a^{\log_a x}=x\)、はいおしまい。

この公式は主に数Ⅲや受験数学で見かけることが多いですが、注目してもらいたいのはココ!
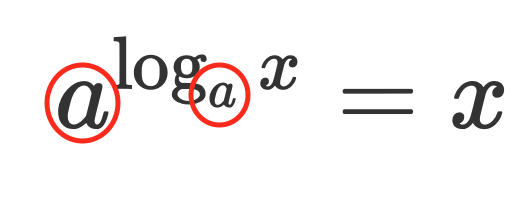
対数乗される数と、対数の底が一致しているときに打ち消しあって真数だけ残るという見方ができます。
見かけることはそう多くないかもしれませんが、数Ⅲでは結構出てきますので、心のどこかにとどめておいてくださいね。
数ⅡB常用対数とは?
常用対数とは、底が10の対数のこと。
常用対数
常用対数・・・\(\log_{10}x\)
この対数を使うことで、おおよその桁数や小数点の位置が求められるようになります。
文系の方は、主に会計などの分野でお世話になることが多く、よく出てくるので”常用”という名前がついています。
人によっては10を略記して\(\log x\)と書く方もいます。

-

-
【感覚で理解できる!】常用対数とは?意味と使い方を徹底解説!!
続きを見る
数Ⅲ自然対数とは? お金儲けで考えよう!
自然対数は、底がネイピア数\(e\)の対数のこと。かなり便利な性質を持っています。
自然対数
自然対数・・・\(\log_{e}x\)
理系の方はこの自然対数の方が、常用対数よりも圧倒的に多く登場します。
そのため理系の方は、\(\log_{e}x\)を\(\log_{}x\)とか、\(\ln x\)と書いたりもします。


自然対数やネイピア数は極限の考えを用いるため、数Ⅲの分野なのですが、直感的な理解がとても簡単。
とんでもなく便利で、大学数学ではノート1ページに100体出てきます。




-



-
自然対数、ネイピア数とは?なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる!!
続きを見る
まとめ


まとめ
⒈ \(\log_a M =p \iff a^p = M\)
⒉ 対数は分解したり、まとめたりできる。
- \(\log_a MN = \log_a M + \log_a N\)
- \(\log_a\frac{M}{N} = \log_a M - \log_a N\)
- \(\log_a M^r = r\cdot \log_a M\)
⒊ 対数は底、真数ともに正であり、底は1ではない(真数条件、底の条件)
対数は指数とセットで覚えることで、より覚えやすく、使い勝手がわかります。
計算で慣れることも大事ですが、指数の意味とも比較しながらしっかり理解すべきです。
以上「対数について」でした。







