【忘れても大丈夫！】サインコサインの変換公式、覚え方とコツ→単位円を描こう！

Today's Topic

$$\cos\left(90^{\circ}+\theta\right) = - \sin \theta$$

$$\sin\left(90^{\circ}+\theta\right) = \cos \theta$$

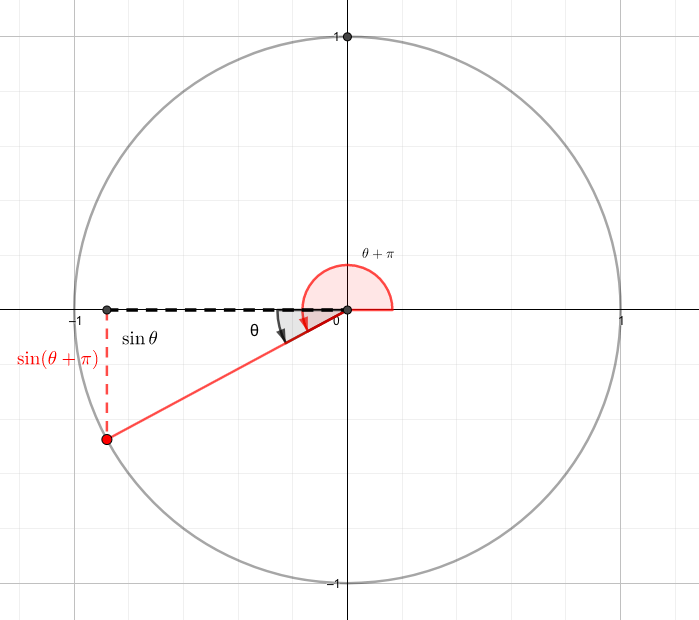
$$\cos\left(180^{\circ}+\theta\right) = - \cos \theta$$

$$\sin\left(180^{\circ}+\theta\right) = - \sin \theta$$

$$\cos\left(-\theta\right) = \cos \theta$$

$$\sin\left(-\theta\right) = - \sin \theta$$

$$\cos\left(90^{\circ}-\theta\right) = \sin \theta$$

$$\sin\left(90^{\circ}-\theta\right) = \cos \theta$$

$$\cos\left(180^{\circ}-\theta\right) = -\cos \theta$$

$$\sin\left(180^{\circ}-\theta\right) = \sin \theta$$

楓

こんなの暗記しようとしちゃダメだよ。。。

小春

サインコサインの問題でね、いろんな変形が出てくるんだけどね、なかなか覚えられないのよぅ・・・

確かに覚えようとすると大変かもね。でも求め方だけ知っておけば、覚えてなくてもOKだよ？

楓

小春

でもいちいち求めると時間かからない？

あぁ、それは大丈夫。多分思い出すのと同じくらいの時間で導出できるよ。絵描くだけだし。

楓

小春

そんなに簡単な覚え方があるなら、ぜひ教えて欲しいな。

この記事を読むと、この問題が解ける！

• \(\cos\left(90^{\circ} - \theta\right) = \sin \theta\)
• \( \sin \left(\theta + 180^{\circ} \right) = -\sin \theta\)
• \(\cos \left(270^{\circ} - \theta\right) = -\sin \theta \)

答えは一番最後にあるよ！

楓

三角関数を一気に理解したい方への記事は、こちらにまとめてあります。

サインコサイン 変換公式｜【事前準備】サインコサイン の意味

まずはサインコサインの図的な意味に着目します。

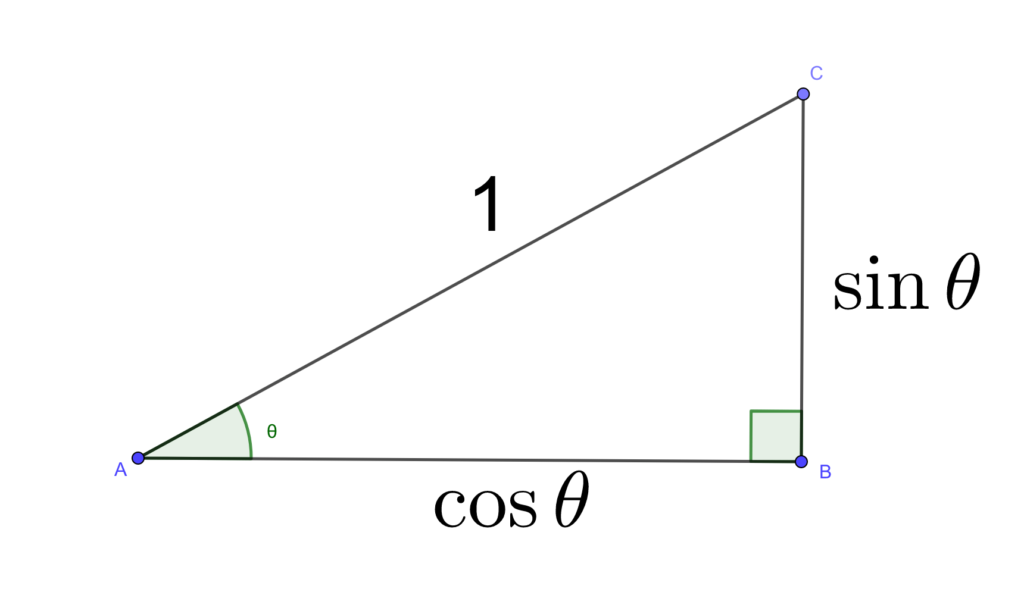
図のように、単位円上にできる直角三角形を考えましょう。

この直角三角形の高さを\(\sin\theta\)、横幅の長さを\(\cos\theta\)と表します。

楓

ただのお名前なんだよね。

サインコサインについて復習したい人はこちらを参考にしてください。

ではこの直角三角形の特徴はなんでしょうか。

それは単位円上にできるということから、斜辺の長さが1であるということ。

すなわち斜辺が1の直角三角形の高さを\(\sin\theta\)、横幅を\(\cos\theta\)といえば良いということがわかります。

楓

僕はこの三角形をベースと呼ぶよ。ベースを探すことで、変換公式は全て、チャチャっと導くことができるよ！

ほんとかなぁ・・・。

小春

サインコサイン 変換公式｜単位円で考える変換公式

では実際にここから、変換公式を導出していきます。

今回のテーマはあくまでも【忘れても大丈夫】なので、暗記に依存する式変形による導出ではなく、図のみを使って導いていきます。

楓

念を押すけど、斜辺が1の直角三角形であるベースを探すことがポイントね！

\(\sin\left(90^{\circ}+θ\right),\cos\left(90^{\circ}+θ\right)\)

単位円周上で\(90^\circ+\theta\)の位置にある点は、図の点Aです。

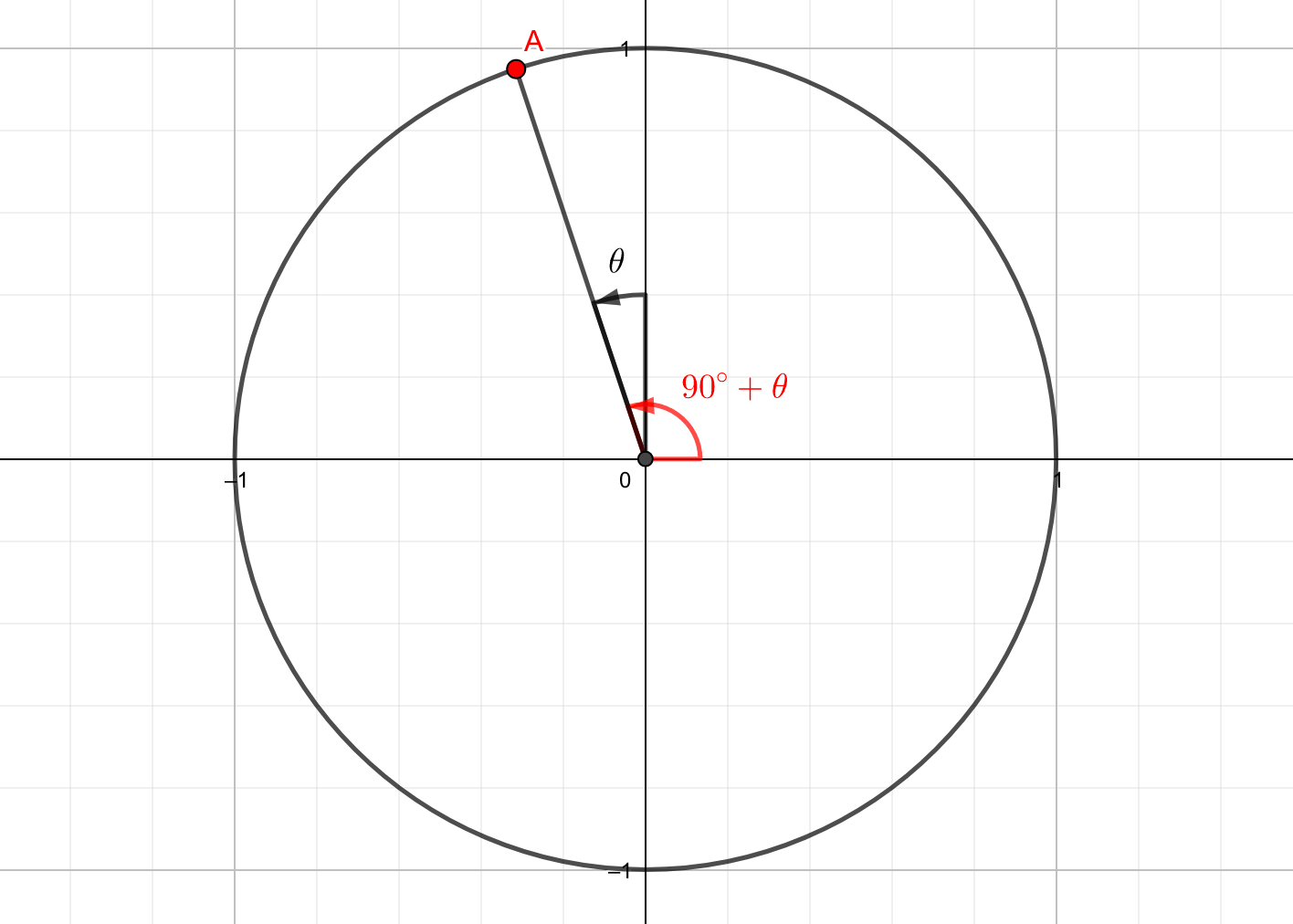
この点Aの座標は、三角関数の定義から\(A\left(\cos\left(90^{\circ}+\theta\right), \sin\left(90^{\circ}+\theta\right)\right)\)と表せます。

小春

点Aは、原点から横に\(\cos\left(90^{\circ}+\theta\right)\)、縦に\(\sin\left(90^{\circ}+\theta\right)\)に動かしたとみなすんだね。

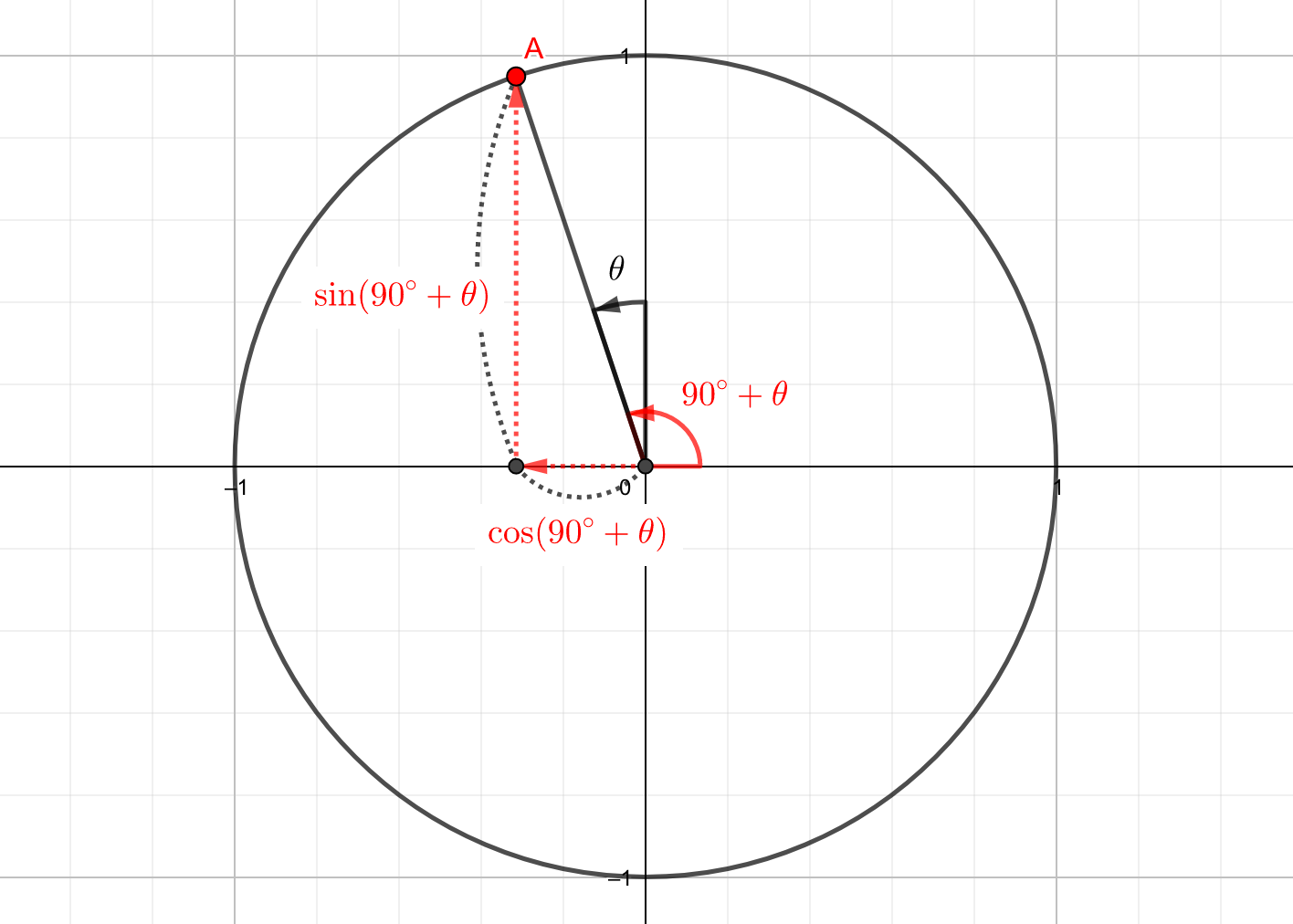
では、ベースの直角三角形を探してみましょう。

すると、色をつけたところにベースがいるのがわかりますね。

小春

\(\triangle AOB\)がベースだね。

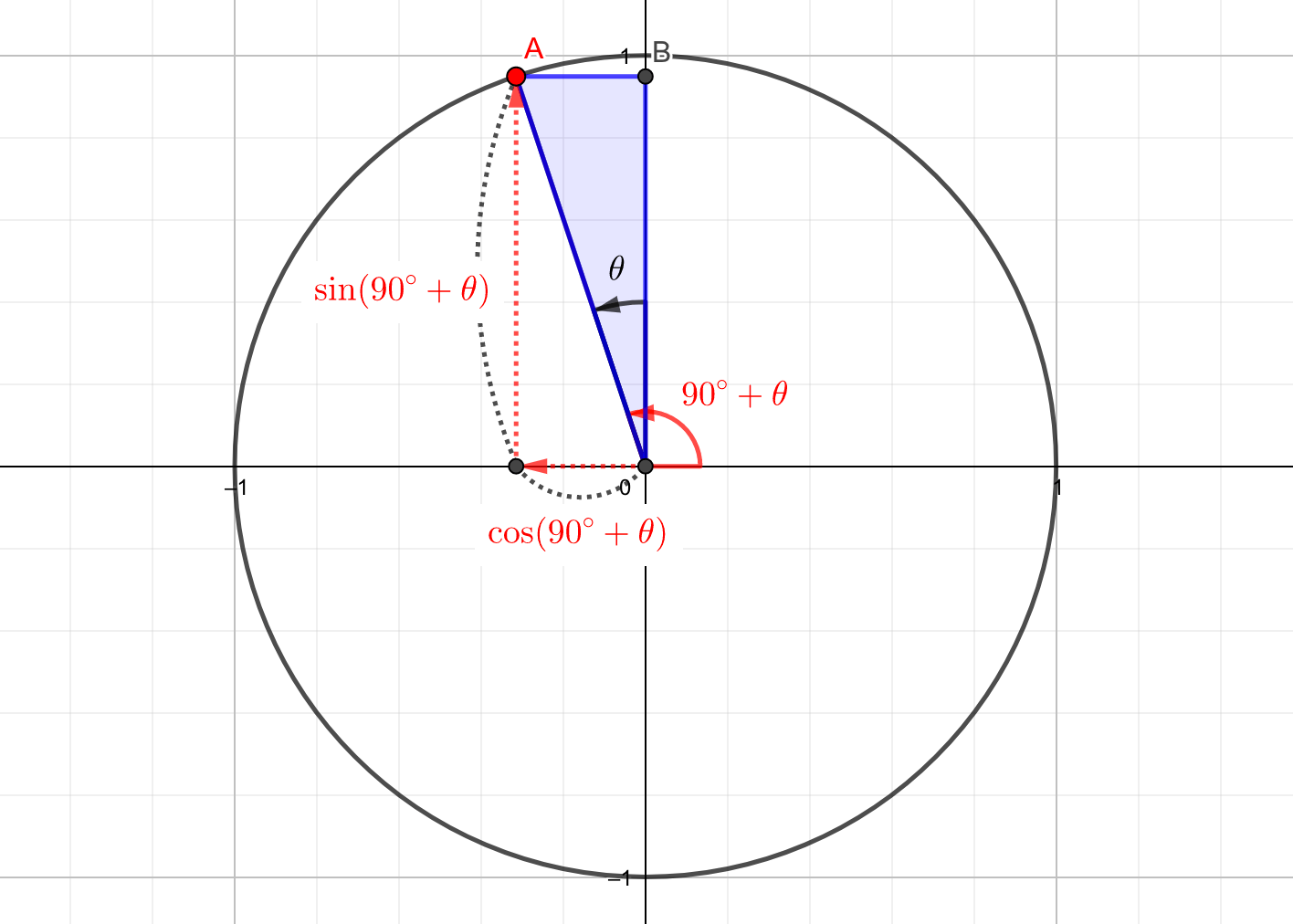
ベースの直角三角形\(\triangle AOB\)を見ると、

と表せますね。

図から、

は明らかです。

つまり

と表せます。

つまり点Aは、\(x\)軸負の方向に\(\sin\theta\)、\(y\)軸正の方向に\(\cos\theta\)だけ動かした点と見ることができます。

よって、

となります。

楓

細かく説明したので長くなったけど、実際に描いてやってみると数秒で終わるよ。

\(\sin\left(180^{\circ}+θ\right),\cos\left(180^{\circ}+θ\right)\)

同じ手順なので、チャチャっと求めていきましょう。

まず、単位円周上の\(180^\circ + \theta \)の位置にある点Aを定めます。

このとき、点Aの座標は\(A\left(\cos\left(180^{\circ}+\theta\right), \sin\left(180^{\circ}+\theta\right)\right)\)と表せます。

楓

原点から横に\(\cos\left(180^{\circ}+\theta\right)\)、縦に\(\sin\left(180^{\circ}+\theta\right)\)に動かした点がAだね。

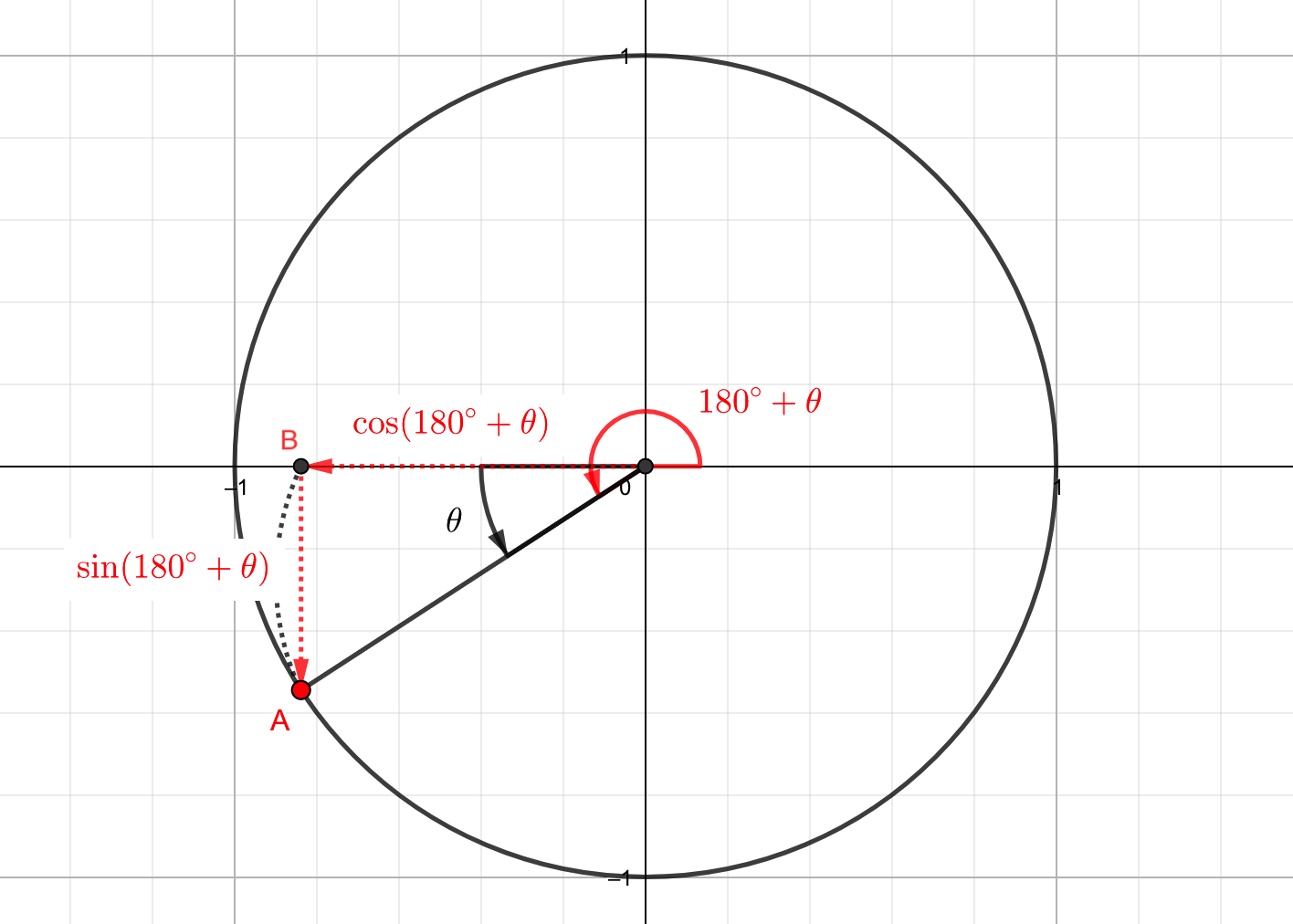
今回のベースは\(\triangle AOB\)と考えることができます。ベースの三角形では

と表せるので、点Aは原点から\(x\)軸の負の方向へ\(\cos \theta\)だけ進み、\(y\)軸の負の方向へ\(\sin \theta\)だけ進んだことがわかります。

よって、

となります。

楓

サインコサインは長さというよりも、座標上の点を表す手法に過ぎないということが大事！

\(\sin(-θ),\cos(-θ)\)

どんどんやっていきましょう。

まず、単位円周上の\(-\theta \)の位置にある点Aを定めます。

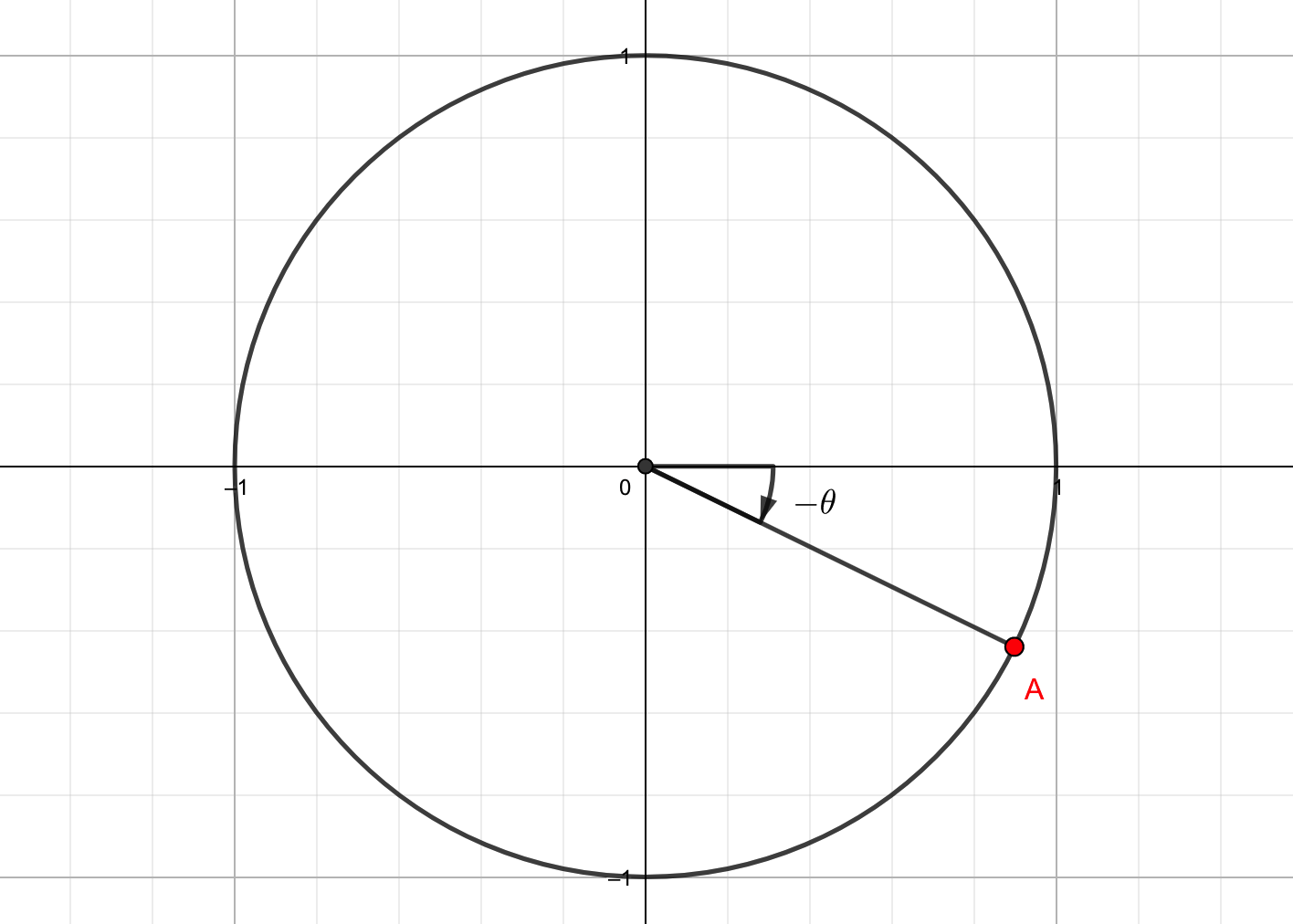
このとき点Aの座標は、\(A\left(\cos\left(-\theta\right), \sin\left(-\theta\right)\right)\)と表せます。

楓

原点から横に\(\cos\left(-\theta\right)\)、縦に\(\sin\left(-\theta\right)\)に動かした点がAだね。

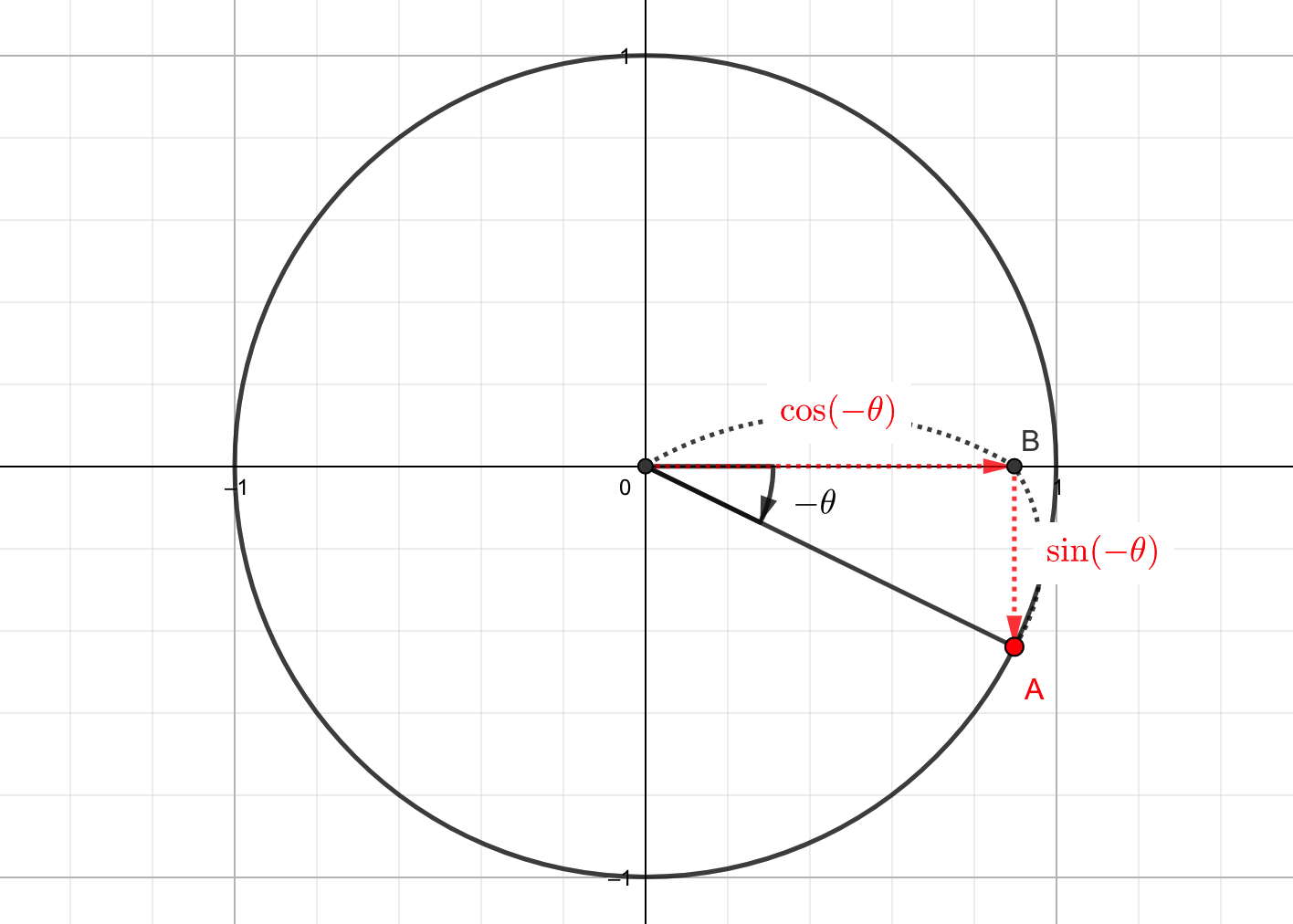
今回もベースは\(\triangle AOB\)と考えることができます。

これにより点Aは、原点からx軸の正の方向へ\(\cos \theta\)だけ進み、y軸の負の方向へ\(\sin \theta\)だけ進んだことがわかります。

よって、

となります。

小春

そろそろ慣れてきたかも！

\(\sin(90^{\circ}-θ)、\sin(90^{\circ}-θ)\)

もう2問やってみましょう。

まず、単位円周上の\(90^{\circ}-\theta \)の位置にある点Aを定めます。

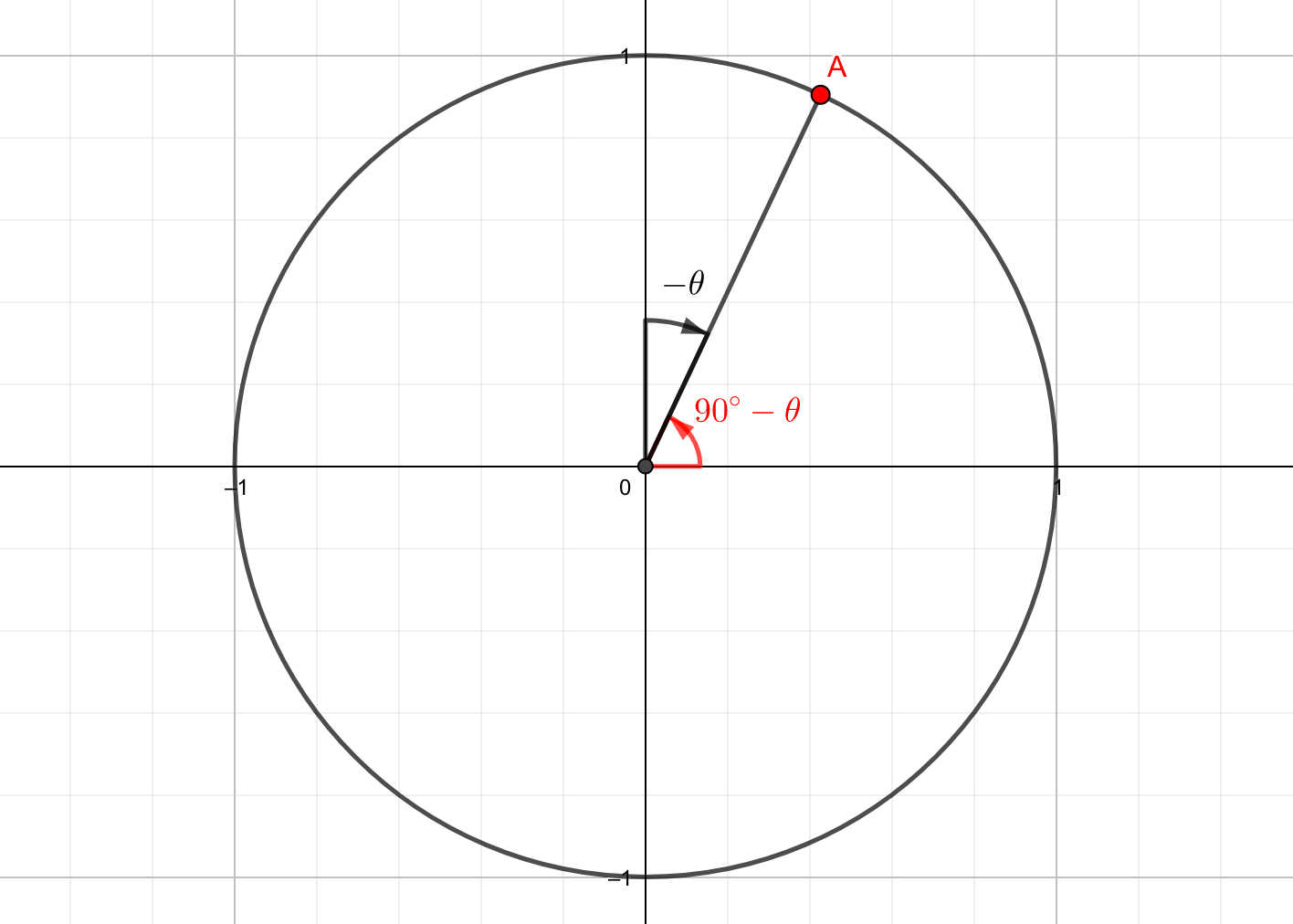
このとき点Aの座標は、\(A\left(\cos\left(90^{\circ}-\theta\right), \sin\left(90^{\circ}-\theta\right)\right)\)と表せます。

楓

原点から横に\(\cos\left(90^{\circ}-\theta\right)\)、縦に\(\sin\left(90^{\circ}-\theta\right)\)に動かした点がAだね。

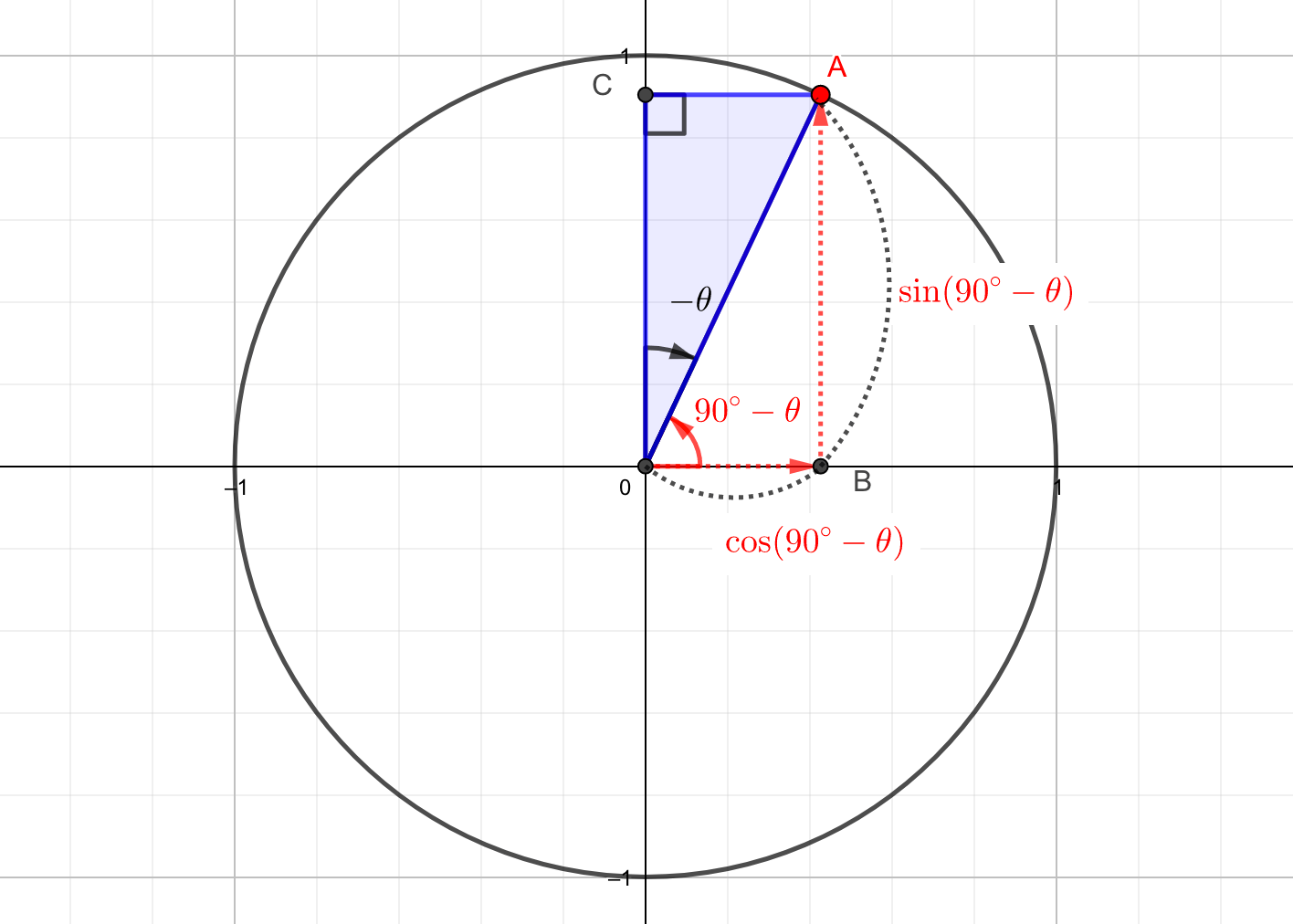
今回のベースは\(\triangle AOC\)と考えることができます。

これにより点Aは、原点から\(x\)軸の正の方向へ\(\sin \theta\)だけ進み、\(y\)軸の正の方向へ\(\cos \theta\)だけ進んだことがわかります。

よって、

となります。

\(\sin(180^{\circ}-θ)、\cos(180^{\circ}-θ)\)

楓

まずは、自分で描いて求めてみよう！

求めてみましたか？それでは一緒に考えていきましょう。

まず、単位円周上の\(180^{\circ}-\theta \)の位置にある点Aを定めます。

このとき、\(A\left(\cos\left(180^{\circ}-\theta\right), \sin\left(180^{\circ}-\theta\right)\right)\)と表せます。

楓

原点から横に\(\cos\left(180^{\circ}-\theta\right)\)、縦に\(\sin\left(180^{\circ}-\theta\right)\)に動かした点がAだね。

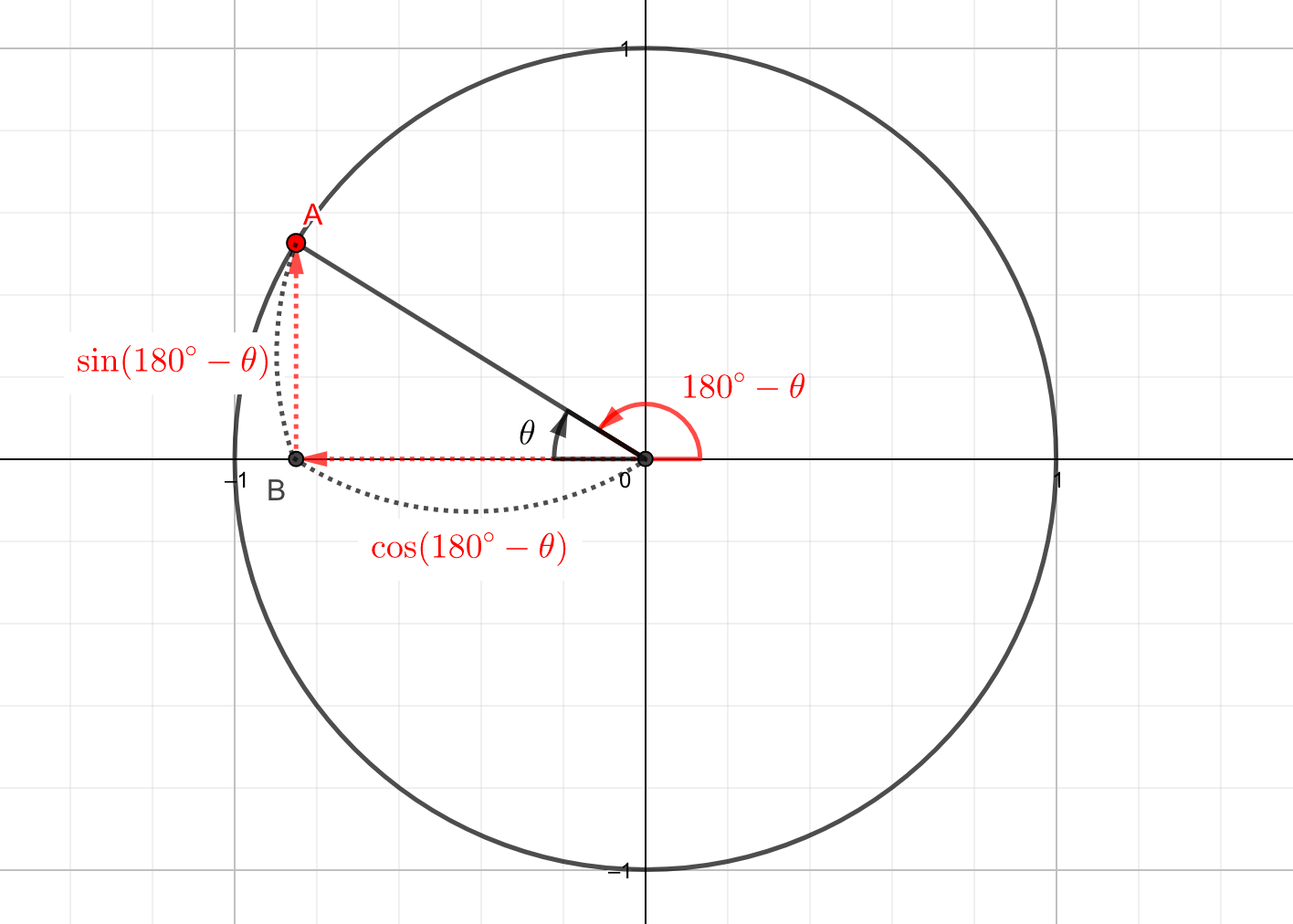
今回のベースは\(\triangle AOB\)と考えることができます。

これにより点Aは、原点から\(x\)軸の負の方向へ\(\cos \theta\)だけ進み、\(y\)軸の正の方向へ\(\sin \theta\)だけ進んだことがわかります。

よって、

となります。

サインコサイン 変換公式｜まとめ

楓

それでは今日のまとめをしておきましょう。

どうでしょうか、暗記するのがバカバカしくなりませんか？

単位円をテキトーに描いて、回転して同じ直角三角形を見つければ、簡単に変換公式を見つけることができます。

こんなアホみたいな変換公式覚えるくらいなら、英単語10個でも覚えてくださいって感じですね。

さぁ、お絵描きをするんだ！

変換公式を知っていると、計算が楽になったり、図的な意味がわかりやすくなります。

これを機に、ぜひマスターしてください。

以上、「サインコサイン 変換公式」についてでした。