Today's Topic
\(y=a\sin\left(kx+p\right)\)のブラフを描くためには、3つの基本をおさえれば良い。





こんなあなたへ
「\(2\sin\left(3x+\frac{\pi}{4}\right)\)のグラフってどういう意味・・・」
「サインコサイン のグラフが複雑すぎて、全く書けない・・・」
この記事を読むと、こんな問題が解ける!
- \(y=2\sin\left(3x+\frac{\pi}{4}\right)\)のグラフを描け。
- \(y=2\sin\left(3x+\frac{\pi}{4}\right)\)のグラフの周期と、最大・最小値を求めよ。

三角関数を一気に理解したい方への記事は、こちらにまとめてあります。
Contents
サインコサインのグラフ|【基本形】\(y=\sin x,y=\cos x\)のグラフ


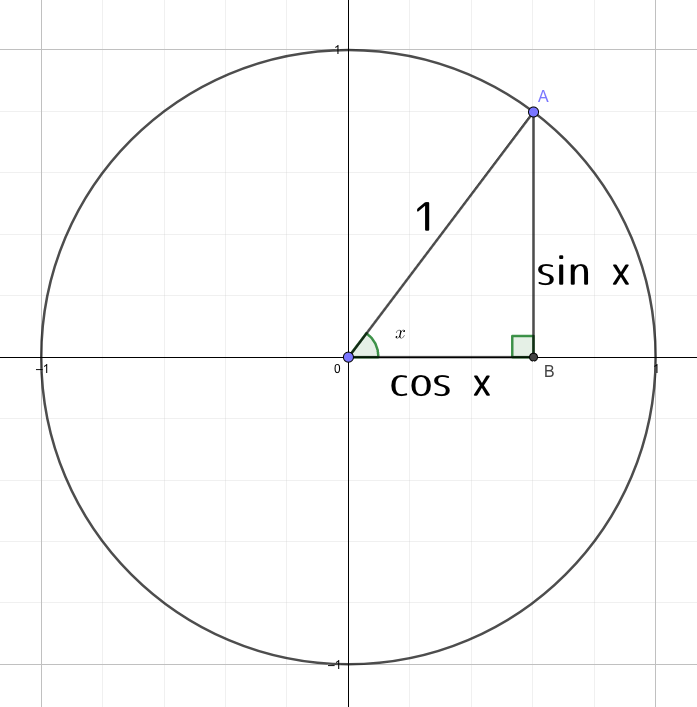

図のような、斜辺1、\(\angle BOA = x\)の直角三角形を考えます。
円周上の点Aの
- \(x\)座標を\(\cos x\)
- \(y\)座標を\(\sin x\)
と表すということを意識しておくと、グラフを区別することがカンタンになります。
について復習したい人はこちらを参考にしてください。
続きを見る



【中学生でもわかった】サインコサインとは?公式を暗記しなくても、感覚でわかる!
サイン、コサインのグラフは次のように、波を描きます。
\(y=\sin x\)のグラフ 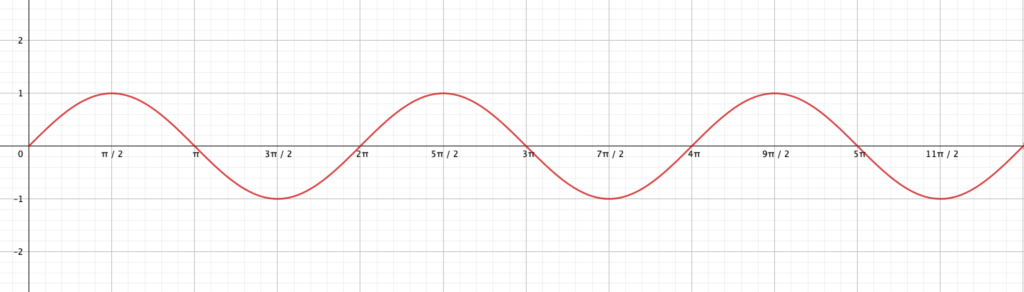



\(y=\cos x\)のグラフ




サインコサイン のグラフの特徴は、次のようなことが挙げられます。
- 波を描く
- サインとコサインのグラフは、\(x\)軸方向に\(\frac{\pi}{2}\)ズレているだけ
- 最大値は(単位円の半径の)1である
- 山と谷2つで、1周期という

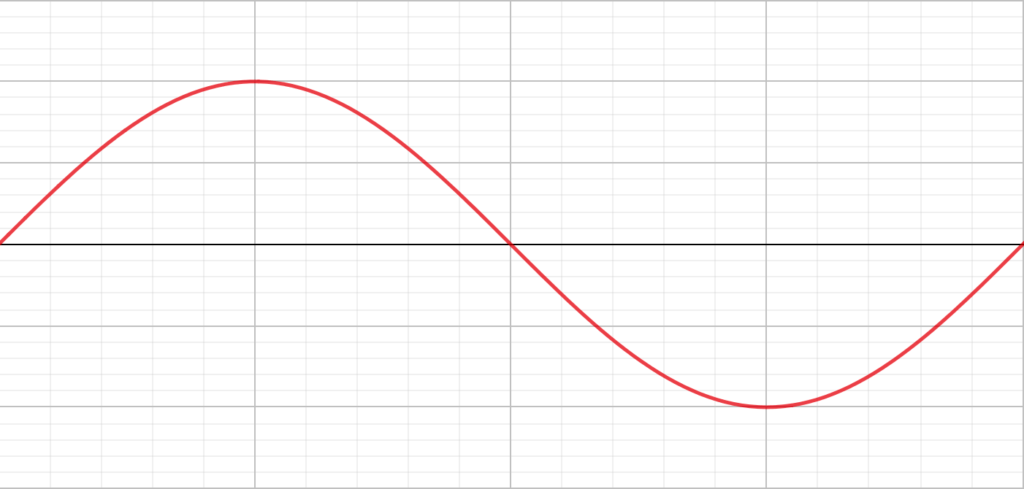
ここからは実際にグラフを見ていきますが、サインとコサインのグラフは\(\frac{\pi}{2}\)ズレているだけで、形は全く一緒。
なので掲載するグラフはサインだけにしておきます。コサインのグラフは頭の中で\(\frac{\pi}{2}\)ズラしてあげてください。
サインコサインのグラフ|\(y=k\sin x,y=k\cos x\)のグラフ


まずはグラフから見ていきます。
\(y=\sin x\)のグラフと\(y=3\sin x\)のグラフを比較してみましょう。
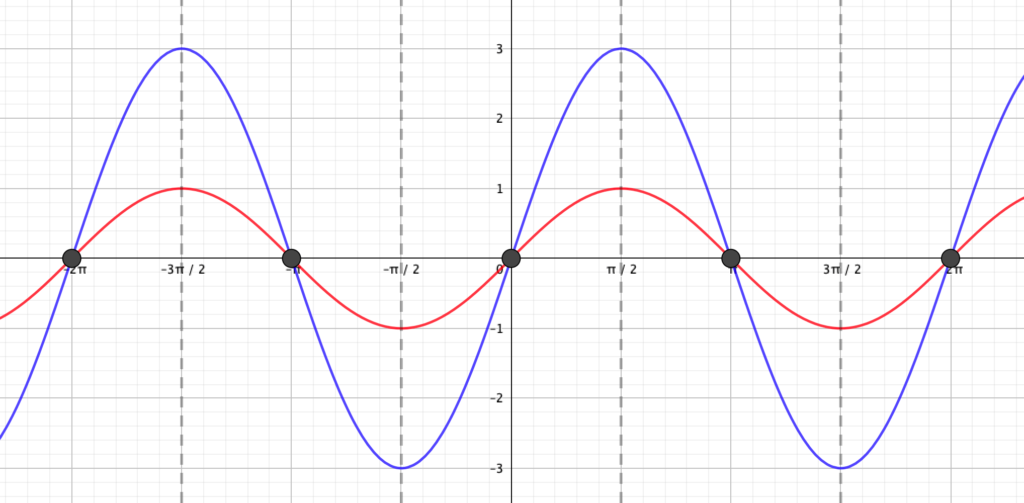

周期や、最大値を取る\(x\)座標などは変化していません。
ところがグラフの形が、より大きな波を描いていることがわかります。


このように、
- \(y=k\sin x\)
- \(y=k\cos x\)
のグラフは、元の\(y=\sin x\)や\(y=\cos x\)のグラフを、縦に\(k\)倍に大きくしたグラフを描く特徴があります。
つまり
ポイント
\(y=k\sin x\)や\(y=k\cos x\)のグラフは、
波の高さをk倍に変える
能力がある!
ということがわかります。
サインコサインのグラフ|\(y=\sin\left(x+a\right),y=\cos\left(x+a\right)\)のグラフ


\(y=\sin x\)と\(y=\sin\left(x+\frac{\pi}{2}\right)\)を比較してみましょう。
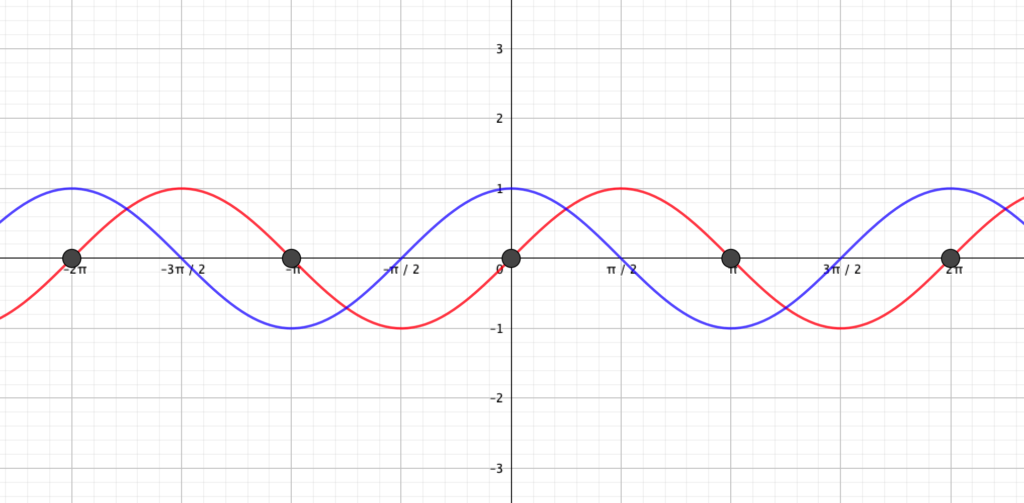

グラフ全体が、\(x\)軸方向に\(-\frac{\pi}{2}\)だけズレました。
これは\(y=\sin x = f(x)\)として捉えると理解しやすいです。
このとき、\(y=\sin \left(x+\frac{\pi}{2}\right)\)は\(y=f\left(x+\frac{\pi}{2}\right)\)と表せます。
ここで思い出して欲しいのは、平行移動の規則。
ポイント
\(y=f(x)\)のグラフを\(x\)軸方向に\(+p\)、\(y\)軸方向に\(+q\)だけ平行移動したグラフの方程式は
$$y-q=f(x-p)$$
と表せる。
平行移動について復習したい人はこちらを参考にしてください。
続きを見る



平行移動のやり方と公式の意味→符号を入れ替えて書き換えるだけで、グラフの問題がスラスラ解ける
つまり、\(y=f\left(x+\frac{\pi}{2}\right)\)と表せる\(y=\sin \left(x+\frac{\pi}{2}\right)\)は、
\(y=\sin x = f(x)\)を横に\(-\frac{\pi}{2}\)だけ平行移動すると言っているのです。


よって
ポイント
\(y=\sin\left(x+a\right),y=\cos\left(x+a\right)\)のグラフは、
グラフを横に\(-a\)だけズラす
という効果がある
ということがわかります。
サインコサインのグラフ|\(y=\sin nx,y=\cos nx\)のグラフ
最後は\(x\)を\(n\)倍したグラフを見てみよう。
例として\(y=\sin x\)と\(y=\sin 3x\)のグラフを、\(x\)の係数に着目して比較してみましょう。
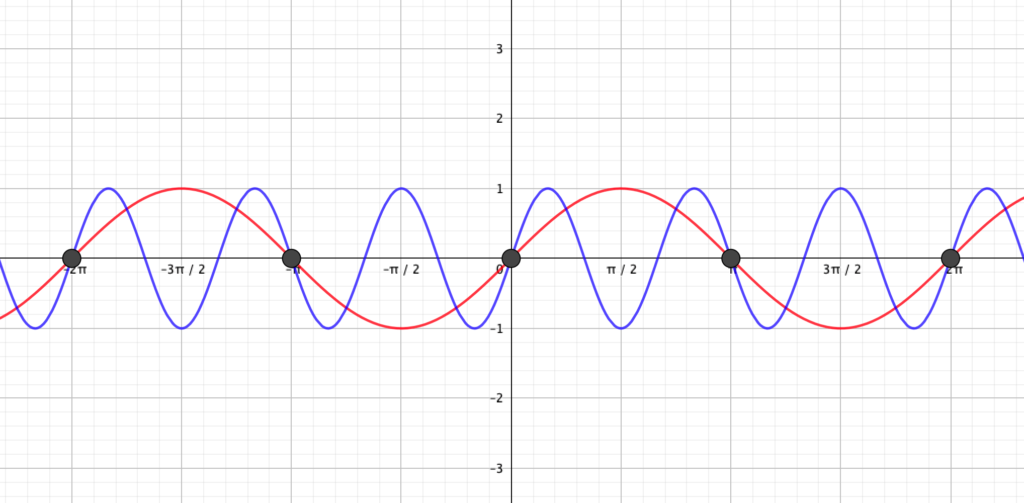

図を見ると、0から\(\pi\)の間に、
- \(y=\sin 1x\) は山が1つ
- \(y=\sin 3x\)は山が3つ
あることがわかります。
この発見から、
- \(y=\sin x\)は1周期が\(2\pi\)
- \(y=\sin 3x\) は1周期が\(\frac{2\pi}{3}\)
と言えますね。


つまり
ポイント
\(y=\sin nx,y=\cos nx\)のグラフは、
- \(0≦x≦\pi\)間に山を\(n\)個つくる
- (山の個数が増えることによって、)1周期の区間が短くなる
という効果がある
ということがわかります。
サインコサインのグラフ|応用例題




例題
\(y=2\sin\left(3x+\frac{\pi}{4}\right)\)の最大値と最小値、周期を求めよ。


まずはグラフを想像してみることにしましょう。
step
1波の高さを2倍してみる。
まず\(y=\sin x\)を2倍して、\(y=2\sin x\)のグラフを考えます。
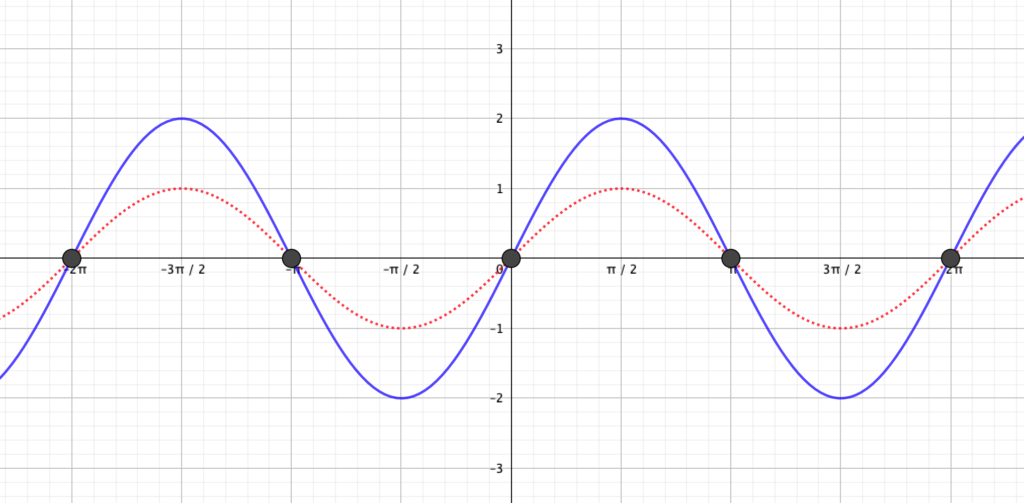



step
2\(x\)を3倍してみる。
次に\(x\)の係数を1から3に変更してみましょう。
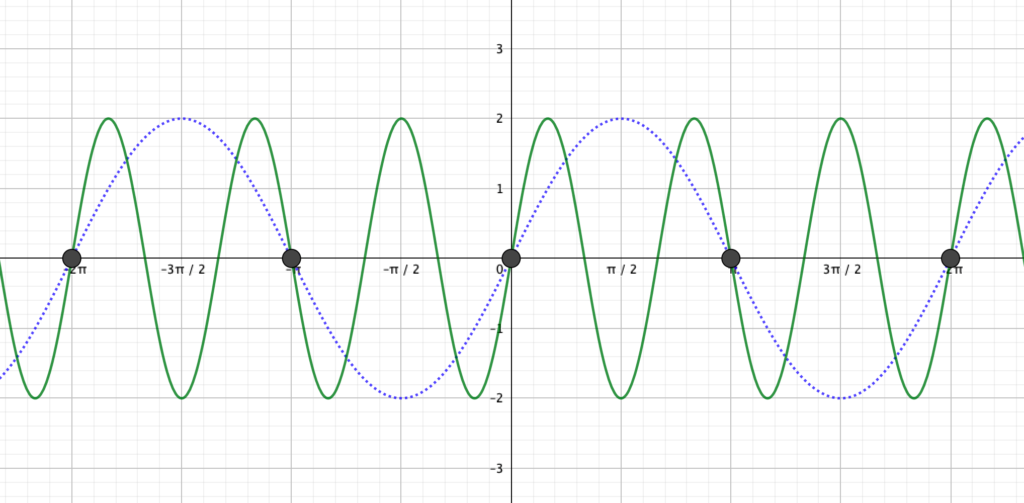







step
3グラフを横にズラしてみる。
最後に平行移動を考えてあげます。
\(y-q=f(x+p)\)のグラフは\(y=f(x)\)のグラフを横に\(-p\)だけ動かすので、\(y=2\sin\left(3x+\frac{\pi}{4}\right)\)のグラフは、\(y=2\sin\left(3x\right)\)グラフを横に\(-\frac{\pi}{4}\)だけズレます。








グラフが想像できてしまえば、あとの問題は楽勝です。
- 最大値:\(y=2\)
- 最小値:\(y=-2\)
- 周期:\(\frac{\pi}{3}\)
はグラフを見たらわかりますね。
ここではSTEP1からSTEP3でグラフを描きましたが、順番はどのステップからやっても構いません。
が、平行移動はなるべく最後にやったほうがパパッと終わる気がします。
サインコサインのグラフ|まとめ


まとめ
- サインとコサインのグラフは、\(\frac{\pi}{2}\)ズレているだけで形は同じ
- \(y=k\sin x\)や\(y=k\cos x\)のグラフは、波の高さを\(k\)倍する
- \(y=\sin\left(x+a\right),y=\cos\left(x+a\right)\)のグラフは、波を横に\(-a\)だけズラす
- \(y=\sin nx,y=\cos nx\)のグラフは、0から\(\pi\)の間に\(n\)個の山を生み出す。
波の高さや周期、平行移動など、式の中の係数はそれぞれ表現するものが違います。
1つ1つの数字が何を表しているか、しっかり見極めて問題を見てみると、サインコサインのグラフは難しくないでしょ?
慣れてくると、紙の端っこにぺぺっと書いて答えがわかるので、ぜひグラフ力を鍛えてください!
以上、「サインコサイン のグラフ」についてでした。









