Today's Topic
$$平均\mu=\frac{x_1+x_2+x_3+\cdots+x_N}{N}$$
(※見切れている場合はスクロール)





こんなあなたへ
「平均点って意味あるの?」
「分散や標準偏差の意味って何?」
Contents
平均の本質|平均の定義とその意味
あなたは平均の公式を覚えていますか?
平均値の求め方
\(x_1,x_2,x_3,\cdots,x_N\)の合計N個のデータがある。これらの値の平均値\(\bar{x}\)は、
$$\bar{x}=\frac{x_1+x_2+x_3+\cdots+x_N}{N}$$
で求められる。
このように算出された平均を相加平均ともいう。
そんな式簡単に覚えられているよ!
全てのデータを足して、データの個数で割ればいいんでしょ?楽チン楽チン!
と言った方は何人もいますが、その度に僕はいつも聞くのです。


具体的な場面で見ていきましょう。
例題
10人の生徒が50点満点数学のテストを受けたところ、
$$10,30,30,10,20,30,10,40,50,20$$
という結果であった。このときの平均を求めよ。
この5人の生徒の点数の平均を求めてみると、
(※見切れている場合はスクロール)
となります。
この結果をもとに

と言われてもなんとなくそんな感じがしますよね?つまりこのときはしっかりと”真ん中”として機能しているようです。
これから先の平均の考え方をわかりやすくするために、棒グラフ(ヒストグラム)を使って視覚的に平均を捉えてみましょう。
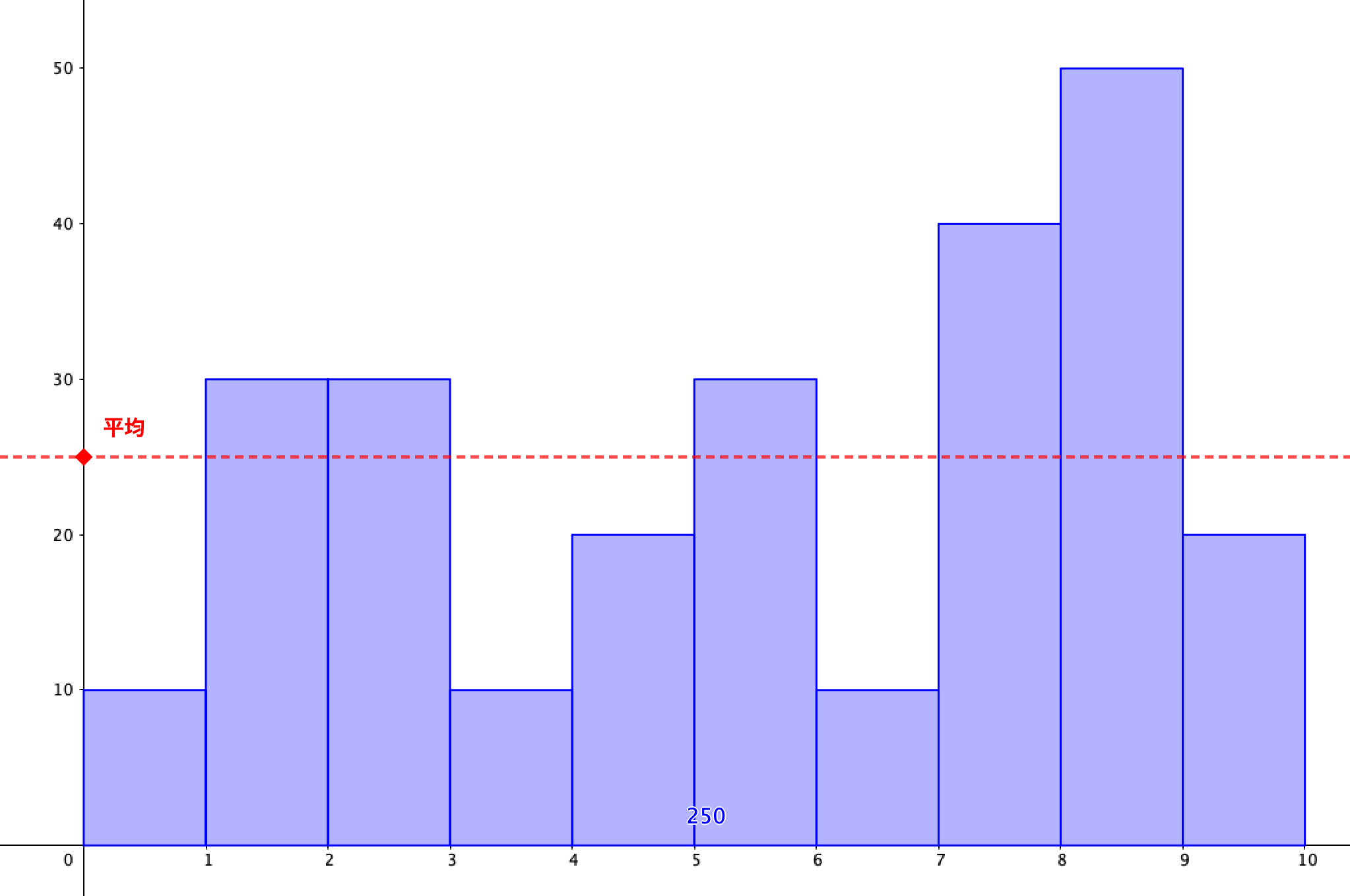
先ほどのデータを柱状グラフにするとこのようになります。
平均よりも上にある長方形と、平均よりも下にある長方形に着目すると、実はこんなことがわかります。
平均よりも上の長方形を、平均よりも下の長方形に分けてあげると、全ての長方形の高さが平均に揃うのです。
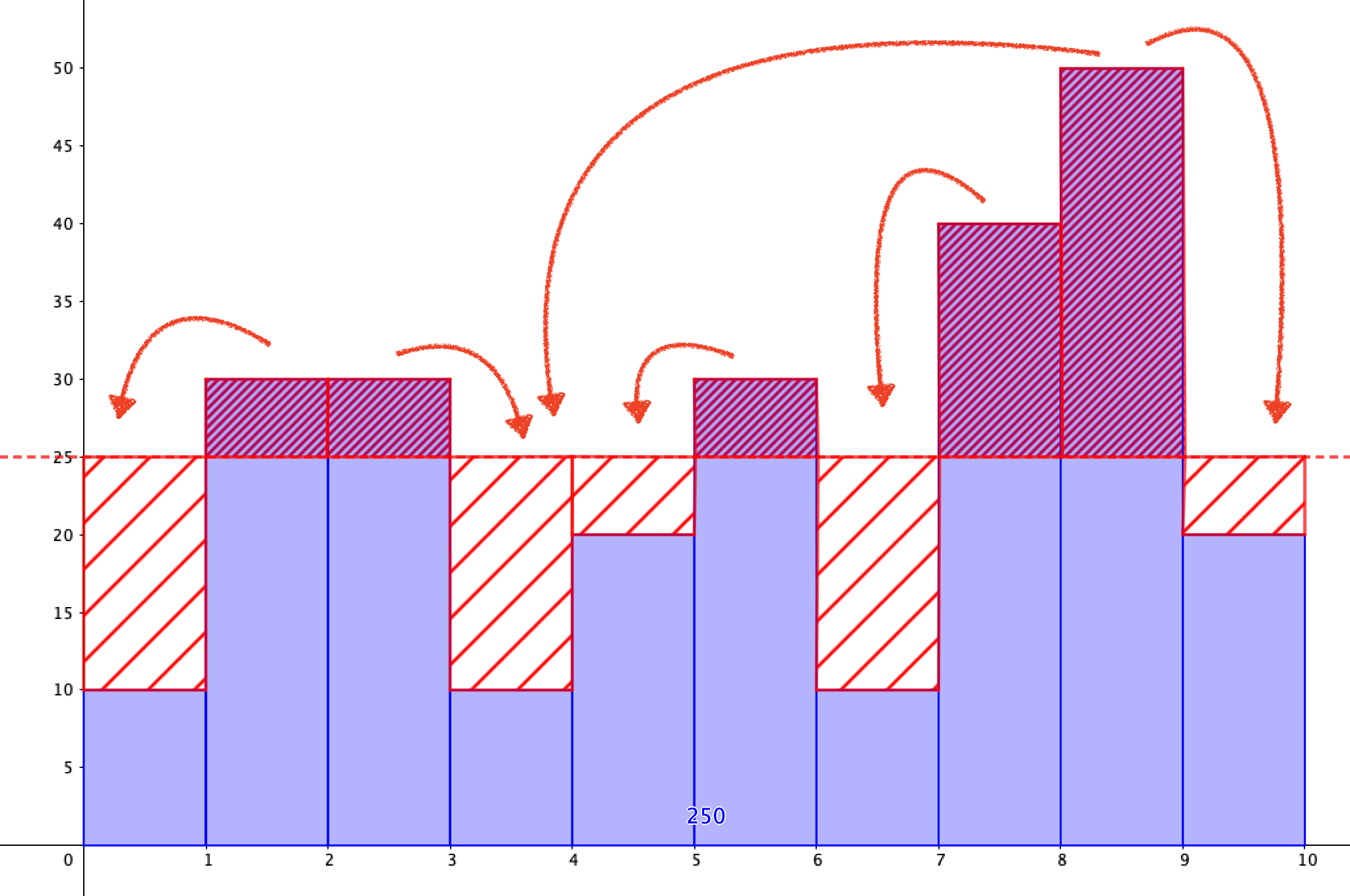


このように平均は、柱状グラフ(ヒストグラム)の凹凸を平らにならす役割を持っています。
この感覚を持っていると、平均のメリットデメリットがよりわかりやすくなります。
平均の本質|平均値を使っても意味がない場面
平均が意味しているのは真ん中だ!
と答える方が非常に多いのですが、本当にそうなのでしょうか?
次の例題を見て、感覚的な”真ん中”かどうか考えてみましょう。
例題
10人の生徒が50点満点数学のテストを受けたところ、
$$10,5,3,10,5,3,2,1,1,50$$
という結果であった。このときの平均を求めよ。
少し極端な例かもしれませんが、この例題では平均が9となります。
この結果を受けて

と言われたらどうでしょう。
あんまり納得いかないのではないでしょうか。
このように平均は極端に大きい値、もしくは小さい値に引っ張られるという弱点があります。
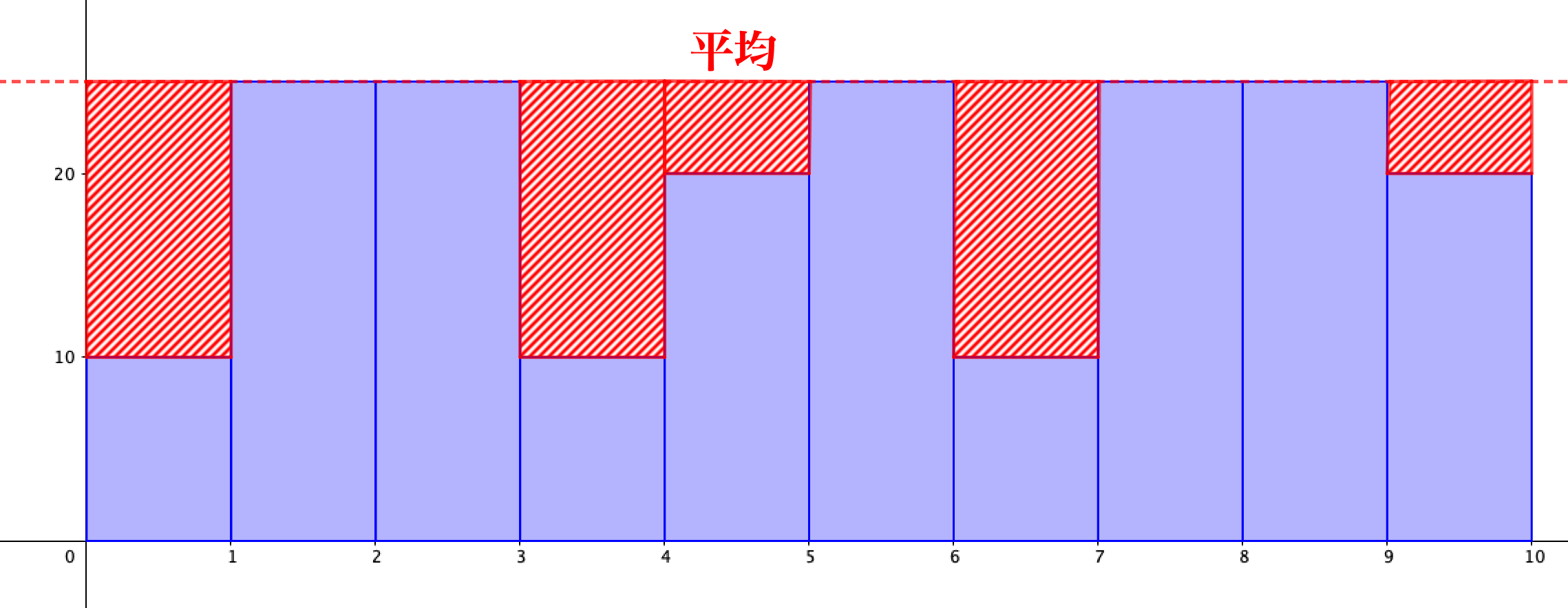
また先ほど同じように柱状グラフを見てみると、わかる通り

- 高さ50の長方形は、大幅に高さがダウン
- 高さが低い長方形は、高さが上昇しやすい
ということがわかります。

以上のことから、平均はデータの値の中に極端に大きな値や、極端に小さな値が混入していると精度が急激に落ちるということがわかります。
そのため平均を利用して何かを考察するときは、その平均を利用するデータの値のばらつき具合が小さいことを確かめて利用するようにしましょう。
平均の本質|有用な平均かどうかを判断するためには分散を使おう

データのばらつき具合を数量的に表した数が分散と呼ばれる値です。
簡単にいうと、『ばらつきレベル』を定義しものです。
ただその公式は、
分散の求め方
N個のデータ
$$x_1,x_2,\cdots,x_N$$
の平均が\(\mu\)のとき、分散\(V\)は次のように求める。
(※見切れている場合はスクロール)
と少々複雑なように見えます。
そこで、分散の値がなぜこのような公式によって求められるのかを考えてみましょう。
この公式を導く過程での気持ちを理解すると、この公式の意味したいことがよくわかります。
分散の求め方
まずは感覚のお話。
例えば2つの資料があります。
資料1
$$3,5,7,5,6,3,4,1,6,4$$
平均:\(4.5\)
資料2
$$1,2,2,1,1,9,10,8,3,3$$
平均:\(4\)
見比べてみると資料2の方がばらつき具合が大きいような気がします。

平均に着目してみると、
- 資料1はどのデータも、平均との差がそれほど大きくない
- 資料2はどのデータも、平均との差が結構大きい
ような印象を受けますね。
つまりデータのばらつき具合を考える上で、平均との差に着目すればうまく数値化できそうです。
そこで『各データと平均の差』の平均を取ってみます。

資料1で考えてみると
(※見切れている場合はスクロール)
となりますが、
は平均を表す式となっています。
よって、
(※見切れている場合はスクロール)
となり、ばらつき具合を求めることができませんでした。
ここでの問題点は負の値が出てきてしまうことです。
式①の分子に着目すると、
というように互いに打ち消しあっている部分がいます。
そこで、負の値が出ないように全ての平均との誤差を2乗することにしましょう。


すると
(※見切れている場合はスクロール)
のようになりました。
同様に資料2のときを求めてみると、
(※見切れている場合はスクロール)
となりました。
よってばらつきレベルは
- 資料1:2.85
- 資料2:11.4
となるので、資料2の方が圧倒的にバラついていることが示せそうです。

このように分散は、
- 各データの値と平均との差を求め、
- それらを2乗し、
- 2乗した値の平均を計算
することで求めることができます。
この気持ちを理解した上でもう一度、分散を求める公式を見てみましょう。
分散の求め方
N個のデータ
$$x_1,x_2,\cdots,x_N$$
の平均が\(\mu\)のとき、分散\(V\)は次のように求める。
(※見切れている場合はスクロール)
このようにして求められる分散の値が小さければ小さいほど、平均は十分納得できる”真ん中”の数として理解できます。
学校によってはテスト返却の際、平均点と一緒に分散を掲載しているところもあり非常に優しい先生だなと感心させられていました(何様だよ。。)
標準偏差の求め方と意味
標準偏差とは、分散にルートをつけた値のことです。
標準偏差の求め方
N個のデータ
$$x_1,x_2,\cdots,x_N$$
の平均が\(\mu\)、分散\(V\)のとき、標準偏差\(s\)は次のように求める。
(※見切れている場合はスクロール)


分散を求める過程の中で、最も重要なのが
を求めている点です。
これはデータのばらつきを求める上で、負の値を出すことを防ぐための対応でした。
ですがこの二乗は、単位に着目すると非常に気持ち悪いことになります。
例題
10人の身長のデータは以下の通り。データのばらつき具合を求めよ。
$$3,5,7,5,6,3,4,1,6,4$$
平均:\(4.5\)
分散を計算すると、2.85\(cm^2\)
身長のデータのばらつき具合を求めていたのに、出てきた「ばらつきレベル」の単位は\(cm^2\)となっていまい、

と違和感が半端ないわけです。
そこでルートをつけることでこの二乗を取り払い、
と標準の単位に揃えるこができます。
平均の本質|色々な平均値

ここでは3つの平均を紹介しますが、最初の度数分布表の平均以外はあまり使う機会がないかもしれません。
度数分布表の平均
(※見切れている場合はスクロール)



| 階級 | 階級値 | 度数 | ||
| 以上 | 〜 | 未満 | ||
| 0 | 〜 | 5 | 2.5 | 4 |
| 5 | 〜 | 10 | 7.5 | 1 |
| 10 | 〜 | 15 | 12.5 | 5 |
| 15 | 〜 | 20 | 17.5 | 4 |
| 20 | 〜 | 25 | 22.5 | 1 |
| 25 | 〜 | 30 | 27.5 | 5 |
- 階級:ある一定の幅を設けた値の区間
- 階級値:階級(設けた区間)の中央値
- 度数:階級内に収まる数が出てきた回数




このような表を度数分布表といいます。
データを羅列するよりも、どの区間の値が一番多いのかなど一目でわかるのでとても有用です。
しかし度数分布表を作成するにあたって、ある重要な情報を切り捨てています。
それはデータの値です。

このとき、平均値を求めようとしても当然データの値がわからないわけですから正確に求めることはできません。
そこで、各階級の階級値と度数の積を求め、それらの値の平均を考えてみます。
すると、
(※見切れている場合はスクロール)
となりました。
度数分布表にする前のデータの羅列の平均を求めてみると、
となり、その後さはわずか0.5ほどしかありません。
一般に生データと度数分布表の平均は一致しませんが、その誤差は無視できる程度のもの。
平均の求め方の亜種として、度数分布表バージョンも覚えておきましょう。
度数分布表の平均
| 階級値 | 度数 |
| \(x_1\) | \(f_1\) |
| \(x_2\) | \(f_2\) |
| \(\cdots\) | \(\cdots\) |
| \(x_N\) | \(f_N\) |
度数の合計(\(f_1+f_2+\cdots+f_N\))が\(n\)のとき、度数分布表の平均は以下のように求める。
$$\frac{x_1f_1+x_2f_2+\cdots +x_Nf_N}{n}$$
相乗平均
相乗平均は、経済や人口の成長率などでよく用いられる平均値です。
2つのデータ\(x_1,x_2\)があるとき、普段よく使う平均は\(\frac{x_1+x_2}{2}\)を計算することで求めます。
しかし、この相乗平均は\(\sqrt{x_1\times x_2}\)で求めます。
相乗平均を求めるためには、2つのデータ\(x_1,x_2\)が正の値である必要があります。
相乗平均をあなたが実際に使う場面というのは、それほど多くないと思います。
人によっては全く使わないものでしょう。
しかし、相加相乗平均と呼ばれる数学の定理はよく使われます。
相加相乗平均
2つの正の値\(a,b\)に対して、
$$\frac{a+b}{2}≧\sqrt{ab}$$
ただし等号が成立するのは\(a=b\)のとき


問題演習でよく出てくる相加相乗平均ですが、何も2つの正の値だけでなく、複数の正の値でも考えることができます。
参考
\(n\)個の正の数\(x_1,x_2,\cdots,x_n\)において、
$$\frac{x_1+x_2+\cdots +x_n}{n}≧\sqrt[n]{x_1x_2\cdots x_n}$$
相加相乗平均の例題
例題
\(x>0\)とする。このとき、次の最小値を求めよ。
$$\left(x+\frac{1}{x}\right)\left(2x+\frac{1}{2x}\right)$$
(慶應義塾大学)

\begin{align} & \ \ \ \left(x+\frac{1}{x}\right)\left(2x+\frac{1}{2x}\right)\\\ &= 2x^2+\frac{1}{2x^2}+\frac{5}{2}\\\ \end{align}
\(2x^2>0,\frac{1}{2x^2}>0\)より、相加相乗平均を用いると
\(\frac{2x^2+\frac{1}{2x^2}}{2}≧\sqrt{2x^2\times\frac{1}{2x^2}}=1\)
よって、
$$2x^2+\frac{1}{2x^2}+\frac{5}{2}≧2+\frac{5}{2}=\frac{9}{2}$$
ただし等号が成立するのは\(2x^2=\frac{1}{2x^2}\)かつ\(x>0\)のとき。
すなわち、\(x=\frac{9}{2}\)のときである。


調和平均

調和平均は以下のように定義されます。
$$\frac{1}{2}\cdot\left(\frac{1}{a}+\frac{1}{b}\right)$$
この平均は速度の平均を求める際に使うことがあります。
が、それよりもちょっと便利なのが以下の不等式です。
調和平均\(≦\)相乗平均\(≦\)相加平均


平均の本質|まとめ

まとめ
- 平均は柱状グラフの凹凸をならしているイメージ
- 平均は値のばらつきが多いと、信用できない
- 値のばらつきを求めるためには、分散を求めれば良い。
- 度数分布表の平均は、生データの平均とは一致しない。
- 文系数学の入試問題で出題される分数関数の最大最小値問題は相加相乗平均の可能性大
今回扱ったように、平均とは絶対に信用できる数値というわけではありません。
ここで大事なのは、だからこそ平均という情報を相手が提示してきたときに疑うということです。
データの表現方法は様々で、人間は自分の都合のいいようにデータを表現します。
そこで提示されたものが本当に適切かどうか、信用するに値するかどうかは受け取り手である私たちが判断しなければなりません。


以上、「平均の本質」でした。








