【三角関数の合成】やり方のコツと意味を徹底解説！複雑な三角関数の問題をラクにしよう！

Today's Topic

$$a\sin\theta+b\cos\theta = \sqrt{a^2+b^2}\sin\left(\theta+\alpha\right)$$

（※見切れている場合はスクロール）

小春

楓くん、三角関数の合成ってなぁに？授業で出てきたけどちんぷんかんぷん。

名前の通り、三角関数は一つにまとめることができるんだ！

楓

小春

一つにまとめる？

そう、例えば$\sin\theta+\cos\theta$という和も$\sin$や$\cos$だけで表現することができるということだよ！

楓

小春

そうなの？！やり方と使う場面を教えて欲しいな！

こんなあなたへ

「三角関数の合成の意味がわからない」

「やり方はわかるけど、やる意味とか使う場面がわからない」

この記事を読むと・・・

三角関数の合成のやり方、そしてコツが簡単に理解できる！
合成をするメリットがわかる！

三角関数を一気に理解したい方への記事は、こちらにまとめてあります。

まとめ記事

: 【三角関数基礎まとめ】暗記0のサインコサイン！本質から使い道まで徹底解説

続きを見る

Contents

1 三角関数の合成｜合成の公式
2 三角関数の合成｜合成の意味とメリット
3 三角関数の合成｜合成のコツ
4 三角関数の合成｜合成を使う場面
- 4.1 三角関数の合成の例題
5 三角関数の合成｜まとめ

三角関数の合成｜合成の公式

三角関数の合成は、以下の公式で表すことができます。

三角関数の合成

$$a\sin\theta+b\cos\theta = \sqrt{a^2+b^2}\sin\left(\theta+\alpha\right)$$

（※見切れている場合はスクロール）

小春

もう何を言っているのか、わからない・・・。

この公式は、サインコサインの値と同様、憶えるべきものではありません。

合成を使いこなすためには、グラフを意識した『三角関数の合成でやりたいこと』を把握する必要があります。

この『三角関数の合成でやりたいこと』を理解した上で、後述するあるコツを身につければ合成は何も難しくありません。

三角関数の合成｜合成の意味とメリット

楓

三角関数の合成は、グラフを意識しましょう。

サインコサインのグラフは、波を描きます。

$xy$平面に$y=\sin x$と$y=\cos x$のグラフを描いてみると、このようになります。

楓

サインとコサインは周期が$\frac{\pi}{2}$ズレているだけで、基本的な形は一緒だよ。

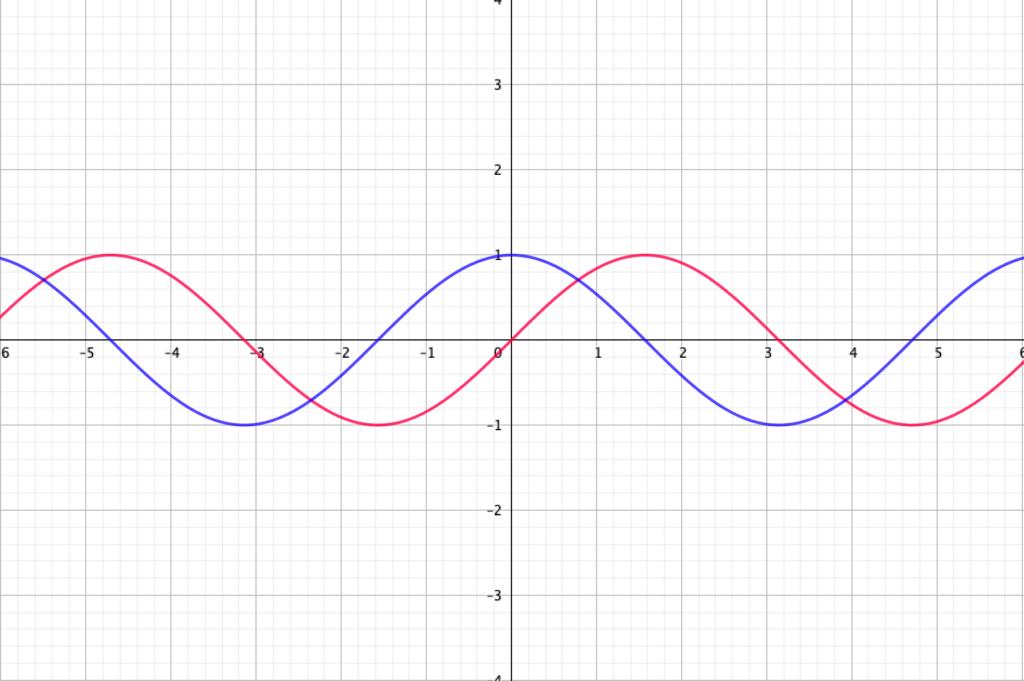
ではここで、二つを足し算した$y=\sin x+\cos x$のグラフを描いてみましょう。

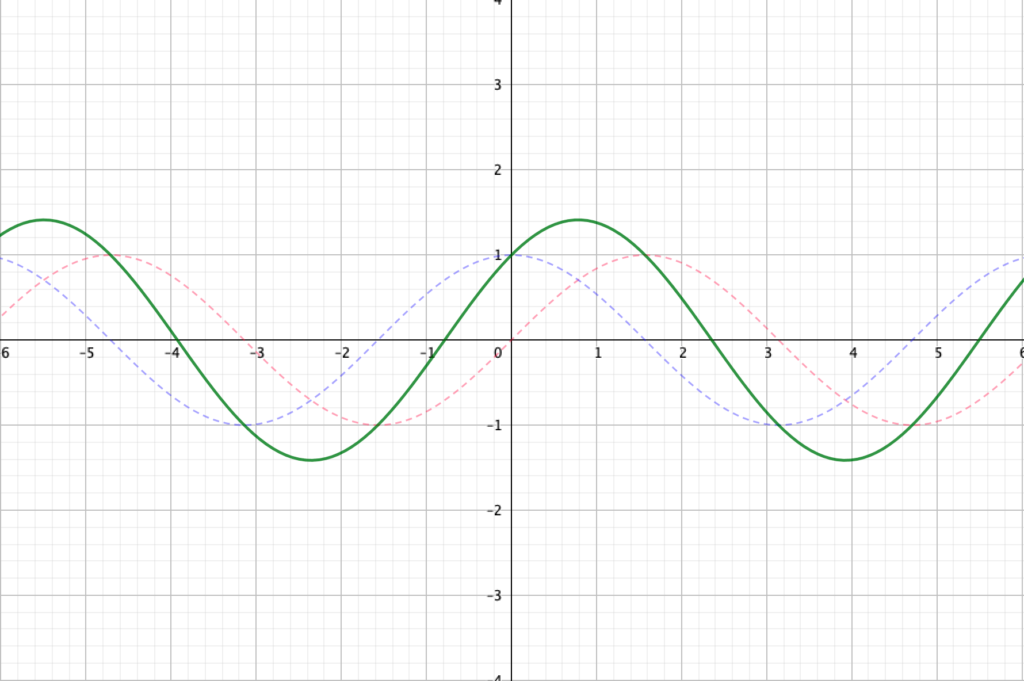
例えば

$x=0$のとき、$\sin 0+\cos 0 = 1$
$x=\frac{\pi}{4}$のとき、$\sin \frac{\pi}{4}+\cos \frac{\pi}{4} = \sqrt{2}$

のように、二つの波が合体してより大きな波を描くことがわかります。

実はこの、2つの波が合体してもまた波ができるという性質がかなり重要です。

これまでに出てきた2つの波は$y=\sin x$と$y=\cos x$の2つ。

$y=\cos x=\sin\left(x-\frac{\pi}{2}\right)$とすることでサインに統一できるので、波は基本的にサインで表すことができるはずです。

楓

このときコサインに揃えても別に構いません。

そこでもう一度、$y=\sin x+\cos x$のグラフを見てみましょう。

2つの波が合体し、より大きな波となっています。

そう！波になっているんです！！！！！

波は基本的にサインで表すことができる、ということがわかっていますので、この$y=\sin x+\cos x$のグラフもサインだけで表したくなるのです。

これが三角関数の合成の意図しているところになります。

要約すると、

ポイント

2つの波が合体すると、波になる。
波はサインの形で表せる。
合体した波も、サインの形で表せるはず！

という考え方です。

楓

コサインの形で表すこともできるけど、テストや入試はサインの形で表すことができれば十分かな。

三角関数の合成｜合成のコツ

例として$y=\sin x+\cos x$の合成を考えていきます。

小春

どうやって合成すればいいか、いまいちピンとこないけどなぁ。

その通り、三角関数の合成には少しだけコツが必要なの。

楓

三角関数の合成の考え方は、三角関数のサインの加法定理の逆をするという認識が最も最適です。

ポイント

$$\sin\left(x+y\right)=\sin x\cos y+\cos x\sin y$$

加法定理について復習したい人はこちらを参考にしてください。

: 加法定理の使い方とイメージしやすい証明→覚えることは２つだけ！

続きを見る

加法定理を眺めてみると、右辺がサインコサイン入り混じった形になっているのに対して、左辺はサインのみで表されています。

つまり加法定理の逆を使えば、僕たちが今一番したいサインのみで表すということができるはずですね。

加法定理の逆

$$\sin x\cos y+\cos x\sin y=\sin\left(x+y\right)$$

ここで、$\sin x+\cos x$と加法定理を見比べてみると、加法定理は$x$と$y$の2変数が登場しているのに対して、$\sin x+\cos x$は$x$の1変数のみです。

そこで加法定理の中で登場した変数のうち1つ$y$が、定数になっていると考えてみます。

つまり$\sin y=定数,\cos y=定数$と考えるわけです。

係数を意識して加法定理を書き換えると、

\begin{align} \sin\left(x+y\right) &= \sin x\cos y+\cos x\sin y\\\ &= \cos y\sin x+\sin y\cos x\\\ \end{align}

となります。

楓

$x\cdot 2+x\cdot 3$を$2x+3x$に書き換えているのと同じことね。

$x$が変数で2、3が定数ね。同じように$\sin x,\cos x$が変数、$\sin y,\cos y$が定数と考えて書き換えるのね。

小春

ここで2つの式を見比べてみましょう。

$$\sin x+\cos x$$
$$\cos y\sin x+\sin y\cos x$$

単純に考えて$\sin x+\cos x$は、$\cos y=\sin y=1$と表された加法定理と考えることができます。

ただし、$\sin x$の係数が$\cos y$、$\cos x$の係数が$\sin y$と考えている点に注意です。

ただ$\cos y=\sin y=1$となる、定数$y$の値は存在しません。

楓

同時に満たすことはできないよね。

そこで、$\sqrt{2}$で$\sin x+\cos x$をくくってみましょう。

$$\sqrt{2}\left(\frac{1}{\sqrt{2}}\sin x+\frac{1}{\sqrt{2}}\cos x\right)$$

このようにすると、$\cos y=\sin y=\frac{1}{\sqrt{2}}$となるような定数$y$を考えればよく、$y=\frac{\pi}{4}$と求められます。

あとは加法定理の逆をたどって

\begin{align} \sin x+\cos x &= \sqrt{2}\left(\frac{1}{\sqrt{2}}\sin x+\frac{1}{\sqrt{2}}\cos x\right)\\\ &= \sqrt{2}\sin\left(x+\frac{\pi}{4}\right)\\\ \end{align}

（※見切れている場合はスクロール）

と合成することができました。

小春

ところで、なんで$\sqrt{2}$でくくろうと思ったの？

この$\sqrt{2}$という値は、$1\sin x+1\cos x$の係数$1,1$を使って

$$\sqrt{1^2+1^2}$$

を計算することで導きました。

このように$\sqrt{係数^2+係数^2}$でくくると、綺麗に合成することができるという認識でOKです。

まとめると、

ポイント

三角関数$a\sin x+b\cos x$の合成を行うためには、$\sin x,\cos x$の係数$a,b$に着目して、$\cos \theta=\frac{a}{a^2+b^2},\sin\theta=\frac{a}{a^2+b^2}$となるような定数$\theta$を見つければ良い。

ということになります。

三角関数の合成｜合成を使う場面

三角関数の合成を使う場面、それは当然サインとコサインが入り混じった関数をよりわかりやすくしたいときです。

例で扱った

$$\sin x+\cos x=\sqrt{2}\left(\sin\left(x+\frac{\pi}{4}\right)\right)$$

も、2つの関数の和から、$\sin x$の定数倍、平行移動を施した形になっています。

楓

具体例を見てみましょう。

三角関数の合成の例題

難易度：

例題

$y=\sin x-\sqrt{3}\cos x\ (0≦x<2\pi)$の最大値と最小値を求めよ。

サインとコサインがバラバラに動くとわかりにくいので、合成して1つのサインと見なせば良い。

$\sin x-\sqrt{3}\cos x$を合成すると、

\begin{align} \sin x-\sqrt{3}\cos x &= \sqrt{1^2+\left(\sqrt{3}\right)^2}\left(\frac{1}{ \sqrt{1^2+\left(\sqrt{3}\right)^2}}\sin x-\frac{\sqrt{3}}{ \sqrt{1^2+\left(\sqrt{3}\right)^2}}\cos x\right)\\\ &= 2\left(\frac{1}{2}\sin x-\frac{\sqrt{3}}{2}\cos x\right)\\\ \end{align}

（※見切れている場合はスクロール）

となる。

よって$\cos \theta=\frac{1}{2},\sin \theta =- \frac{\sqrt{3}}{2}$となるような定数$\theta$が存在する。

$\theta=\frac{5}{3}\pi$はこの条件を満たすので、

$$2\left(\frac{1}{2}\sin x-\frac{\sqrt{3}}{2}\cos x\right)=2\sin\left(x+\frac{5}{3}\pi\right)$$

（※見切れている場合はスクロール）

$-1≦\sin\left(x+\frac{5}{3}\pi\right)≦1$より、

$-2≦2\sin\left(x+\frac{5}{3}\pi\right)≦2$。

よって$\sin x-\sqrt{3}\cos x$の最大値は2、最小値は-2となる。

補足

\begin{align} y &= \sin x-\sqrt{3}\cos x\\\ &= 2\sin\left(x+\frac{5}{3}\pi\right)\\\ \end{align}

より、グラフは次のようになることがわかります。

楓

$y=2\sin x$を横に$-\frac{5}{3}\pi$だけズラしたグラフになっているよ。

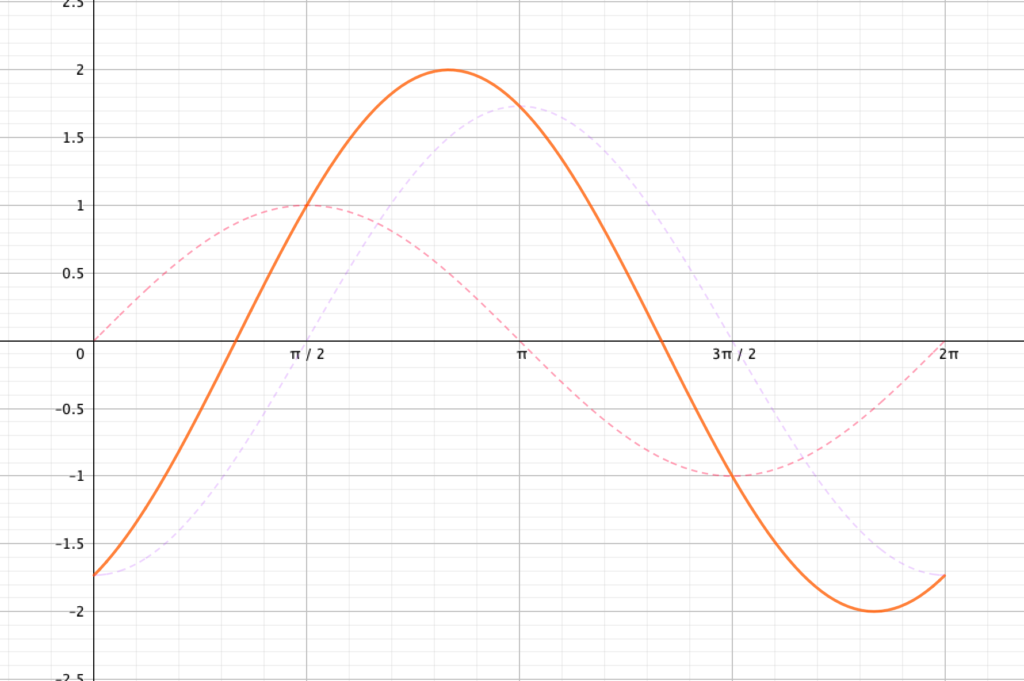
また、$2\sin\left(x+\frac{5}{3}\pi\right)$において

$\sin\left(x+\frac{5}{3}\pi\right)=1$のとき、最大値2となる。

すなわち、

$$x+\frac{5}{3}\pi=\frac{\pi}{2},\frac{5\pi}{2},\frac{9\pi}{2}\cdots$$

よって、

$$x=-\frac{7}{6}\pi,\frac{5}{6}\pi,\frac{17}{6}\pi,\cdots$$

となるが、$0≦x<2\pi$より$x=\frac{5}{6}\pi$のとき最大値を取るとわかる。

最小値も同様にして、$x=\frac{11}{6}\pi$のとき最大値を取るとわかる。

三角関数の合成｜まとめ

それでは、まとめです。

まとめ

三角関数の合成は複数の波を1つの波として、サインで統一して表すためのもの。
三角関数$a\sin x+b\cos x$の合成を行うためには、$\sin x,\cos x$の係数$a,b$に着目して、$\cos \theta=\frac{a}{a^2+b^2},\sin\theta=\frac{a}{a^2+b^2}$となるような定数$\theta$を見つければ良い。
サインコサインが入り組み、考えることが複雑になるものは合成してサインで考えれば良い。

暗記するだけじゃ全く使い道がわからなかったものが、意味を考えると何をすればいいか見えてくるでしょう？

テスト前は暗記でもいいですが、普段勉強するときは暗記よりも意味を意識してみてくださいね。

以上、「三角関数の合成」についてでした。

【三角関数の合成】やり方のコツと意味を徹底解説！複雑な三角関数の問題をラクにしよう！

【三角関数基礎まとめ】暗記0のサインコサイン！本質から使い道まで徹底解説

三角関数の合成｜合成の公式

三角関数の合成｜合成の意味とメリット

三角関数の合成｜合成のコツ

加法定理の使い方とイメージしやすい証明→覚えることは２つだけ！

三角関数の合成｜合成を使う場面

三角関数の合成の例題

三角関数の合成｜まとめ

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則