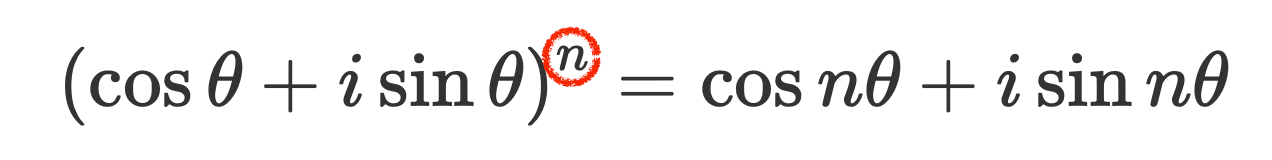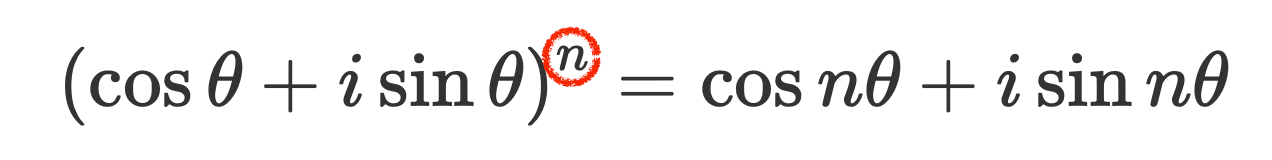Today's Topic
$$\left(\cos\theta+i\sin\theta\right)^n=\cos n\theta+i\sin n\theta$$

小春
楓くん、ド・モアブルの定理の使い道とか、意味がいまいち掴めなくて・・・
その定理は僕がドモアブるって動詞にするくらいよく使うよ!

楓

小春
えぇ〜、そんな使うの?!やっぱ証明からやった方が良い?
証明は帰納法の練習になるし、演習を積むことで使い方もわかるよ。じゃあ今回は、この2つをメインに解説するね!

楓
こんなあなたへ
「ド・モアブルの定理って、どんな問題が出るの?」
「ド・モアブルの定理の証明が知りたい!」
この記事を読むと、この問題が解けるようになる!
- \(\left(\frac{1}{\sqrt{3}+i}\right)^{10}\)
- \( \left(\cos\theta+i\sin\theta -1\right)^n\)

楓
複素数を一気に理解したい方への記事は、こちらにまとめてあります。
ド・モアブルの定理とは|使える場面など
ド・モアブルの定理
どんな整数\(n\)でも
$$\left(\cos\theta+i\sin\theta\right)^n=\cos n\theta+i\sin n\theta$$
が成り立つ。
一般にどんな複素数も極形式
$$r\left(\cos\theta+i\sin\theta\right)$$
の形で表すことができるので、ド・モアブルの定理は複素数の〜乗を計算する際に用います。
ド・モアブルの定理の証明|3STEP
では、ド・モアブルの定理の証明について解説していきたいと思います。
ド・モアブルの定理は、数学的帰納法で証明します。

楓
あえて証明を扱うのは、数学的帰納法の力がつくからなんだよね。
ド・モアブルの定理を証明する上で着目すべきなのが、『指数\(n\)がどんな数なのか』です。

小春
まずここでは、指数法則を調べる際と同じことを考えます。
指数\(n\)が自然数の数であれば、指数を考える上では何も問題ありませんが、0や負の数で成り立つかどうかは考える必要があります。
そこで、以下のステップに分けて証明していきます。
- 指数\(n\)が自然数のとき
- 指数\(n\)が0のとき
- 指数\(n\)が負の数のとき

楓
一気に考えることができないから、分けて考えていくよ。

小春
STEP1|指数\(n\)が自然数のとき
すべての自然数\(n\)において、
$$\left(\cos\theta+i\sin\theta\right)^n=\cos n\theta+i\sin n\theta$$
が成り立つことを数学的帰納法で示す。
\(n=1\)のとき、
\begin{align} 左辺 &= \left(\cos\theta+i\sin\theta\right)^1\\\ &= \cos \theta+i\sin \theta\\\ \end{align}
\begin{align} 右辺 &= \cos 1\theta+i\sin 1\theta\\\ &= \cos \theta+i\sin \theta\\\ \end{align}
(※見切れている場合はスクロール)
よって、左辺=右辺が成立するので、\(n=1\)のときは成立する。
\(n=k\ (k=2,3,4\cdots)\)のとき成り立つと仮定すると、
$$\color{red}{\left(\cos\theta+i\sin\theta\right)^k=\cos k\theta+i\sin k\theta}$$
(※見切れている場合はスクロール)
が成り立つはずである。
\(n=k+1\)のとき、
\begin{align} 左辺 &= \left(\cos\theta+i\sin\theta\right)^{k+1}\\\ &= \left(\cos\theta+i\sin\theta\right)^1\cdot\color{red}{\left(\cos\theta+i\sin\theta\right)^k}\\\ &= \left(\cos\theta+i\sin\theta\right)^1\cdot\color{red}{\left(\cos k\theta+i\sin k\theta\right)}\\\ \end{align}
(※見切れている場合はスクロール)
これを展開する。
\begin{align} \left(\cos\theta+i\sin\theta\right)\cdot\left(\cos k\theta+i\sin k\theta\right) &= \cos\theta\cos k\theta+i\cos\theta\sin k\theta +i\sin\theta\cos k\theta-\sin\theta\sin k\theta\\\ &= \left(\cos\theta\cos k\theta-\sin\theta\sin k\theta\right)+i\left(\sin\theta\cos k\theta+\cos\theta\sin k\theta\right)\\\ \end{align}
(※見切れている場合はスクロール)
ここで、加法定理の逆を考えると
$$\cos\theta\cos k\theta-\sin\theta\sin k\theta = \cos(\theta+ k\theta)$$
$$\sin\theta\cos k\theta+\cos\theta\sin k\theta = \sin(\theta+ k\theta)$$
(※見切れている場合はスクロール)
となる。
よって、
\begin{align} (与式) &= \cos(\theta+ k\theta)+i \sin(\theta+ k\theta)\\\ &= \cos(1+k)\theta+i \sin(1+k)\theta\\\ \end{align}
(※見切れている場合はスクロール)
となり、\(n=k+1\)のときも成立する。
以上より、すべての自然数\(n\)において、ド・モアブルの定理は成立することが示された。

楓
ここではまだ\(n=1,2,3,\cdots\)のときしか言ってないよ。
STEP2|指数\(n\)が0のとき
\((複素数)^0=1\)であるとする。
\(n=0\)のとき、
\begin{align} 左辺 &= \left(\cos\theta+i\sin\theta\right)^0\\\ &= 1\\\ \end{align}
\begin{align} 右辺 &= \cos 0+i\sin 0\\\ &= 1+0i\\\ \end{align}
(※見切れている場合はスクロール)
よって、左辺=右辺が成立するので、\(n=0\)のときは成立する。

楓
ただしここでは\((複素数)^0=1\)が定義されていることに注意してね。

小春

楓
STEP3|指数\(n\)が負の数のとき
\((複素数)^{-1}=\frac{1}{複素数\ \ }\)であるとする。
\(n<0\)のときを考える。\(n=-m\ (m>0)\)とすると、
$$\left(\cos\theta+i\sin\theta\right)^n=\frac{1}{\left(\cos\theta+i\sin\theta\right)^n}$$
となる。
つまり\(n<0\)のとき、ド・モアブルの定理が成り立つことを示すには、
$$\frac{1}{\left(\cos\theta+i\sin\theta\right)^m}=\cos (-m\theta)+i\sin (-m\theta)$$
(※見切れている場合はスクロール)
を示せば良い。
\(m=1\)のとき
\begin{align} 左辺 &= \frac{1}{\left(\cos\theta+i\sin\theta\right)}\\\ &= \frac{1\color{blue}{\times\left(\cos\theta-i\sin\theta\right)}}{\left(\cos\theta+i\sin\theta\right)\color{blue}{\times\left(\cos\theta-i\sin\theta\right)}}\\\ &= \cos\theta-i\sin\theta\\\ &= \color{blue}{\cos (-\theta)+i\sin (-\theta)}\\\ \end{align}
\begin{align} 右辺 &= \cos (-1\theta)+i\sin (-1\theta)\\\ &= \cos \theta-i\sin \theta\\\ \end{align}
(※見切れている場合はスクロール)
よって、左辺=右辺が成立するので、\(m=1\)のときは成立する。

楓
分母が複素数のときは、共役な複素数をかけて実数化してあげよう!
\(m=k\ (k=2,3,4\cdots)\)のとき成り立つと仮定すると、
$$\color{red}{\frac{1}{\left(\cos\theta+i\sin\theta\right)^k}=\cos (-k\theta)+i\sin (-k\theta)}$$
(※見切れている場合はスクロール)
が成り立つはずである。
\(m=k+1\)のとき、
\begin{align} 左辺 &= \frac{1}{\left(\cos\theta+i\sin\theta\right)^{k+1}}\\\ &= \frac{1}{\left(\cos\theta+i\sin\theta\right)}\cdot\color{red}{\frac{1}{\left(\cos\theta+i\sin\theta\right)^k}}\\\ &= \frac{1\color{blue}{\times\left(\cos\theta-i\sin\theta\right)}}{\left(\cos\theta+i\sin\theta\right)\color{blue}{\times\left(\cos\theta-i\sin\theta\right)}}\cdot\color{red}{\left(\cos (-k\theta)+i\sin (-k\theta)\right)}\\\ &= \color{blue}{\left(\cos (-\theta)+i\sin (-\theta)\right)}\cdot\color{red}{\left(\color{red}{\cos (-k\theta)+i\sin (-k\theta)}\right)}\\\ \end{align}
(※見切れている場合はスクロール)
これを展開する。
\begin{align} \left(\cos (-\theta)+i\sin (-\theta)\right)\cdot\left(\cos (-k\theta)+i\sin (-k\theta)\right) &= \cos(-\theta)\cos (-k\theta)+i\cos(-\theta)\sin (-k\theta) +i\sin(-\theta)\cos (-k\theta)-\sin(-\theta)\sin (-k\theta)\\\ &= \left(\cos(-\theta)\cos (-k\theta)-\sin(-\theta)\sin (-k\theta)\right)+i\left(\cos(-\theta)\sin (-k\theta) +\sin(-\theta)\cos (-k\theta)\right)\\\ \end{align}
(※見切れている場合はスクロール)
ここで、加法定理の逆を考えると
$$\cos(-\theta)\cos (-k\theta)-\sin(-\theta)\sin (-k\theta)= \cos(-\theta- k\theta)$$
$$\cos(-\theta)\sin (-k\theta) +\sin(-\theta)\cos (-k\theta) = \sin(-\theta- k\theta)$$
(※見切れている場合はスクロール)
となる。
よって、
\begin{align} (与式) &=\cos(-\theta- k\theta)+i \sin(-\theta- k\theta)\\\ &= \cos\left(-(1+k)\theta\right)+i \sin\left(-(1+k)\theta\right)\\\ \end{align}
(※見切れている場合はスクロール)
となり、\(n=k+1\)のときも成立する。
以上より、すべての自然数\(m\)において、成立することが示された。
- 指数\(n\)が自然数のとき
- 指数\(n\)が0のとき
- 指数\(n\)が負の数のとき
いずれの場合も成立したので、すべての整数\(n\)において、ド・モアブルの定理は成り立つ。
『自然数→0→負の数』と数の世界を拡大することで、整数のとき成り立つかを考えるという手法は、よく使われる手です。

楓
問題で『整数』とあったら0の場合も負の場合も成り立つか考えてみるといいよ。
帰納法では、『整数で成り立つ』→『自然数のとき、0&負のとき別々で示すといい』ってことね!

小春
ド・モアブルの定理|身につく問題
ここでは、ド・モアブルの定理を使えるようになる思考力を鍛えます。
のメニューで行きます。

楓
ド・モアブルが使える形に持ち込むために、どんな変形をすればいいかを考えよう。
問題1
難易度:
例題
\(\left(\frac{1}{\sqrt{3}+i}\right)^{10}\)の値を求めよ。
まず、分数だと〜乗を考えるのがダルいので
\(\left(\frac{1}{\sqrt{3}+i}\right)^{10}=(\sqrt{3}+i)^{-10}\)
に変形します。
ド・モアブルの定理は指数が負でも、整数であれば成り立つので、この式に適用していきます。
ただしドモアブるためには、複素数を極形式の形で表す必要があります。
\begin{align} (\sqrt{3}+i)^{-10} &= \left(2\left(\frac{\sqrt{3}}{2}+\frac{1}{2}i\right)\right)^{-10}\\\ &= 2^{-10}\left( \cos \frac{ \pi }{6}+i \sin \frac { \pi }{6} \right)^{-10}\\\ \end{align}
(※見切れている場合はスクロール)

楓
\begin{align} 2^{-10}\left(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\right)^{10} &= 2^{-10}\left(\cos\frac{-10\pi}{6}+i\sin\frac{-10\pi}{6}\right)\\\ &= 2^{-10}\left(\cos\frac{-5\pi}{3}+i\sin\frac{-5\pi}{3}\right)\\\ \end{align}
(※見切れている場合はスクロール)

楓
ここが答えでもいいと思うのですが、さらに変形することもできます。
\begin{align} 2^{-10}\left(\cos\frac{-5\pi}{3}+i\sin\frac{-5\pi}{3}\right) &= 2^{-10}\left(\frac{1}{2}+\frac{\sqrt{3}}{2}\right)\\\ &= 2^{-11}(1+3i)\\\ \end{align}
(※見切れている場合はスクロール)

楓
問題の指示や、その後に続く問題の形式でどちらを答えにするか判断すればいいよ。
問題2
難易度:
例題
\(\left(\left(\sqrt{6}-\sqrt{2}\right)+\left(\sqrt{6}+\sqrt{2}\right)i\right)^{10}\)の値を求めよ。
先ほどの問題でも扱ったように、ドモアブるためには極形式で表す必要があります。
ところがこの問題、いきなり極形式に表そうとすると地獄になります。
実は複素数と極形式には、
- 複素数:計算しやすい
- 極形式:図が意識しやすい、ドモアブれる
という、使い分けがあります。
つまり、
ポイント
極形式で考えることができない、あるいはめんどくさい場合は、ある程度複素数の形で処理してから極形式にすれば良い。
ということです。実際に見てみましょう。
\begin{align} \left(\left(\sqrt{6}-\sqrt{2}\right)+\left(\sqrt{6}+\sqrt{2}\right)i\right)^{10} &= \left(\left(\left(\sqrt{6}-\sqrt{2}\right)+\left(\sqrt{6}+\sqrt{2}\right)i\right)^2\right)^5\\\ &= \left(-4\sqrt{12}+8i\right)^5\\\ &= 8^5\left(-\sqrt{3}+i\right)^5\\\ \end{align}
(※見切れている場合はスクロール)
ここで、中身が綺麗な極形式で表せるか試してみましょう!
\begin{align} -\sqrt{3}+i &= -2\left(\frac{\sqrt{3}}{2}-\frac{1}{2}i\right)\\\ &= -2\left(\cos\left(-\frac{\pi}{6}\right)+i\sin\left(-\frac{\pi}{6}\right)\right)\\\ \end{align}
(※見切れている場合はスクロール)
うまくいきました。ということは・・・

楓
\begin{align} (与式) &= 8^5\times(-2)^5\left(\cos\left(-\frac{5\pi}{6}\right)+i\sin\left(-\frac{5\pi}{6}\right)\right)\\\ &= -2^{20}\left(-\frac{\sqrt{3}}{2}-\frac{1}{2}i\right)\\\ &= 2^{19}\left(\sqrt{3}+i\right)\\\ \end{align}
(※見切れている場合はスクロール)
問題3
難易度:
例題
\(\left(\cos\theta+i\sin\theta-1\right)^n\)を極形式の形で求めよ。
くどいようですが、ドモアブれるのは極形式のときのみ。
今回の場合は-1が邪魔で極形式になっていませんので、すぐにドモアブるわけにはいきません。
ここが工夫のポイント!あなたはどう-1を処理しますか?
ここで、
$$-1=\cos\pi+i\sin\pi$$
であることに着目しましょう。
すると、
\begin{align} \left(\cos\theta+i\sin\theta-1\right)^n &= \left(\cos\theta+i\sin\theta+(\cos\pi+i\sin\pi)\right)^n\\\ &= \left((\cos\theta+\cos\pi)+i(\sin\theta+\sin\pi)\right)^n\\\ \end{align}
(※見切れている場合はスクロール)
と変形できます。
目指すは極形式\(r(\cos\theta+i\sin\theta)\)の形です。
この形はコサインとサインでまとまっていることが大きな特徴。
つまり\(\cos\theta+\cos\pi,\ \sin\theta+\sin\pi\)がコサインとサインでひとまとまりになってくれたら嬉しいわけです。
そこで和積の公式を使ってみましょう。
和積の公式
- $$\sin A+ \sin B = 2\sin\frac{A+B}{2}\cos \frac{A-B}{2}$$
- $$\cos A+ \cos B = 2\cos\frac{A+B}{2}\cos \frac{A-B}{2}$$
和積の公式について復習したい人はこちらを参考にしてください。
すると、
$$\cos\theta+\cos\pi=2\cos\frac{\theta+\pi}{2}\cos\frac{\theta-\pi}{2}$$
$$\sin\theta+\sin\pi=2\sin\frac{\theta+\pi}{2}\cos\frac{\theta-\pi}{2}$$
(※見切れている場合はスクロール)
となります。
よって、
\begin{align} \left((\cos\theta+\cos\pi)+i(\sin\theta+\sin\pi)\right)^n &= \left(2\cos\frac{\theta+\pi}{2}\cos\frac{\theta-\pi}{2}+2i\sin\frac{\theta+\pi}{2}\cos\frac{\theta-\pi}{2}\right)^n\\\ &= \left(2\cos\frac{\theta-\pi}{2}\right)^n\left(\cos\frac{\theta+\pi}{2}+i\sin\frac{\theta+\pi}{2}\right)^n\\\ &= \left(2\sin\frac{\theta}{2}\right)^n\left(\cos\frac{\theta+\pi}{2}n+i\sin\frac{\theta+\pi}{2}n\right)\\\ \end{align}
(※見切れている場合はスクロール)
となります。

楓
答えが複雑ですが、しっかりと極形式の形で表せているのでOKです。
この問題で押さえておきたいポイントは、
ポイント
- ドモアブるためには、極形式の形で表す必要がある。
- 極形式の形で表すためには、2倍角や半角、和積の公式や積和の公式を用いて変形すれば良い。
です。
ド・モアブルの定理|まとめ

楓
まとめ
・ド・モアブルの定理を証明するためには
- \(n\)が自然数のとき
- \(n\)が0のとき
- \(n\)が負の整数のとき
の順に、数学的帰納法を用いれば良い。
・ドモアブるためには、
極形式の形で表せば良い。
・極形式の形にするためには、
- ある程度、複素数の形で処理をすれば良い。
- 倍角や半角、和積や積和などの公式から変形すれば良い。
ド・モアブルの定理は複素数の累乗を考える上で、絶対に必要になります。
実は複素数はこれまでの累乗とは異なり、不気味な性質を見せてくれます。
それも全てはド・モアブルの定理で説明できます。
内容自体はそれほど難しくなく、極形式に変形できるかどうかがポイントになります。
和積など忘れかけていた人はこのタイミングでぜひ復習しておきましょう。
以上、「ド・モアブルの定理について」でした。