Today's Topic
対数の性質
- \(\log_a a = 1\)
- \(\log_a 1 = 0\)
- \(\log_a a^p = p\)
- \(a^{\log_a b} = b\)
は、「真数は底の〜乗」というのがパッと思い浮かばない時だけ使えば良い。



参考【対数の定義】公式で覚えるな!対数とは何か、定義で理解すれば大丈夫!
この記事を読むと、この意味がわかる!
- $$\log_2 \frac{1}{32}$$
- $$\left(\sqrt{2}\right)^{\log_2 5}$$

Contents
対数の重要条件は5つ!
対数は、その定義から次の4つの重要な性質が生まれました。
ポイント
- \(\log_a a = 1\)
- \(\log_a 1 = 0\)
- \(\log_a a^p = p\)
- \(a^{\log_a b} = b\)
また、この性質とは他に『真数条件』という、とても重要な性質(というか条件)もあるのですが、これは対数の定義からではなく、対数関数の定義から生まれたものなので、別の記事でじっくり解説していきたいと思います。
それでは、今回は対数の定義から導かれる4つの性質をみていくことにしましょう。

\(\log_a a = 1\)
対数といえば、対数の定義でご紹介したように、とりあえず\(\log_2 8 = 3\)を思い出してみましょう。
参考【対数の定義】公式で覚えるな!対数とは何か、定義で理解すれば大丈夫!
\(\log_2 8\)は、「8は2の何乗?」と聞いているだけで、\(\log_2 8 = 3\)はそれが3乗であることを述べています。
では適当な数\(a\)に対して、\(\log_a a\)は何を聞いているのでしょうか?


\(a\)を複数回掛けたら\(a\)になりました。さて、\(a\)は何回かけたでしょうか?
と聞かれたら、それは当然1回ですね。
よって、
が得られるわけです。
\(\log_a 1 = 0\)
さて、先ほどと全く同じように、対数を日本語に訳していきますよ〜。
\(\log_a 1\)はなんと訳せるでしょうか?

ここで重要になるのは、指数法則です。
指数が整数にまで拡大したとき、数学では
を定義として定めていましたね。
参考【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則
よって、〜乗して1になったという場合には、

以上より、
が得られました。
\(\log_a a^p = p\)
ジャンジャンいきましょう。
左辺を日本語訳してみましょうか。


よって、
が得られました。
今回は底と真数がどちらも\(a\)の場合を扱いましたが、底と真数が異なる場合では
が成り立ちます。
これは対数の計算法則で紹介しますが、これも対数の定義から導出することが可能です。

参考【対数の計算法則】なぜ掛け算が足し算に?対数の計算は定義を見返そう!
\(a^{\log_a b} = b\)
さて、この性質は対数の定義でもご紹介したのですが、結構重要ですので再度説明しておきますね。
まず指数部分にある対数ですが、日本語訳してみると、、、

これにより\(\log_a b = t\)とおくと\(a\)は\(t\)乗すると\(b\)になることがわかります。

では\(\log_a b = t\)とおいたので、与式も\(t\)に置き換えてみましょう。
\(\log_a b = t\)とおくと\(a\)は\(t\)乗すると\(b\)になると言っていたので、
が得られます。
結局これは、\(\log_a b\)が『\(a\)が\(b\)になるための指数』を表していることに気づけば、\(a\)をその指数乗すれば\(b\)になるのは当然ですよね?


対数の定義から考えてみれば当たり前のことを言っているだけですね?
ただ理解はできるけど、覚えにくいなぁという方は次のような理解をしてみたらどうでしょうか。
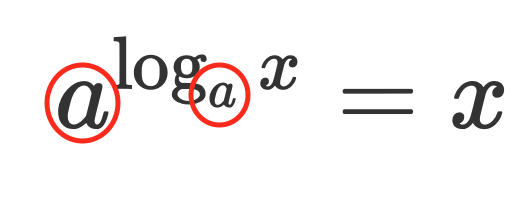
このように対数乗される数と、対数の底が一致しているときに打ち消しあって真数だけ残るという見方ができます。
対数の計算は、めんどくさい時だけ性質に持ち込む
対数の性質は、ご覧の通り基本的に対数の定義さえ覚えていれば、何も必死になって覚えることはありません。
むしろ頭の片隅にある必要すらなく、
「\(\log_3 1\)って、1は3の何乗ですかって聞いてるな?じゃあ0やろ。」
というように、今まで通り定義を思いだせば何も問題ありません。
ただ例外があります。
それは計算速度を上げたい場合です。
対数の性質は、
「対数の定義に帰着したときにちょ〜っと考えるのめんどくさいなぁ」
といった場合に、式で解決することができるようになります。
それでは例題です。
例題
$$\log_\sqrt{3} 81$$

このように、パッと「真数は底の〜乗だっ★」と答えがわからない場合、性質が使えるまで式変形を施して強引に解くことができます。

ただし念を押しておくと、この性質に持ち込む手法は
ということです。
多少めんどくさても、テスト以外の時ではなるべく「真数は底の〜乗」を意識して暗算できるようになったほうが、こんなしょうもない性質覚えるよりよっぽど効果的です。
まとめ

まとめ
対数の性質
- \(\log_a a = 1\)
- \(\log_a 1 = 0\)
- \(\log_a a^p = p\)
- \(a^{\log_a b} = b\)
は、「真数は底の〜乗」というのがパッと思い浮かばない時だけ使えば良い。
どんな計算にもすぐに公式暗記を使う人ほど、数学はのびません。
今回のご紹介した性質を「あくまで計算速度にこだわりたい時だけ」と限定したのは、この性質は定義から考えれば当たり前すぎて、わざわざ覚える必要がないからです。
無駄な努力より、結果を出す努力をしましょう。
以上、「対数の性質について」でした。
チェック問題
例題
$$\log_2 \frac{1}{32}$$




ということは\(\frac{1}{32}\)は2の\(-5\)乗ってわかりますね。
あらら、定義から出しちゃいました。



例題
$$\left(\sqrt{2}\right)^{\log_2 5}$$
これも本来であれば対数の定義から導出できるんですが、ちょっとややこしいですね。
計算ミスをするくらいであれば、今回の性質を使ってみましょうか。









