Today's Topic
\(\sin\theta,\cos\theta\)とはなんなのか。
なぜ\(\sin^2\theta + \cos^2\theta = 1\)が成り立つのか。




こんなあなたへ
「サインコサインなんて暗記でしょ?」
「覚える公式が多くて嫌い、何しているかもわかんないし」
この記事を読むと・・・
- サインコサイン の意味や使い道が、図で簡単にわかる!
- サインコサイン の値を暗記しなくても、自分で秒速で求められる!
三角関数を一気に理解したい方への記事は、こちらにまとめてあります。
Contents
サインコサイン基本講座|【意味を理解しよう】サインは高さ、コサインは横幅








なので、まずはサインコサインを使いたくなる気持ちを理解していきましょう。
理解した上で定義を見てみると、そういうことか!とすぐに理解できるようになります。




まず、下の図をみてください。
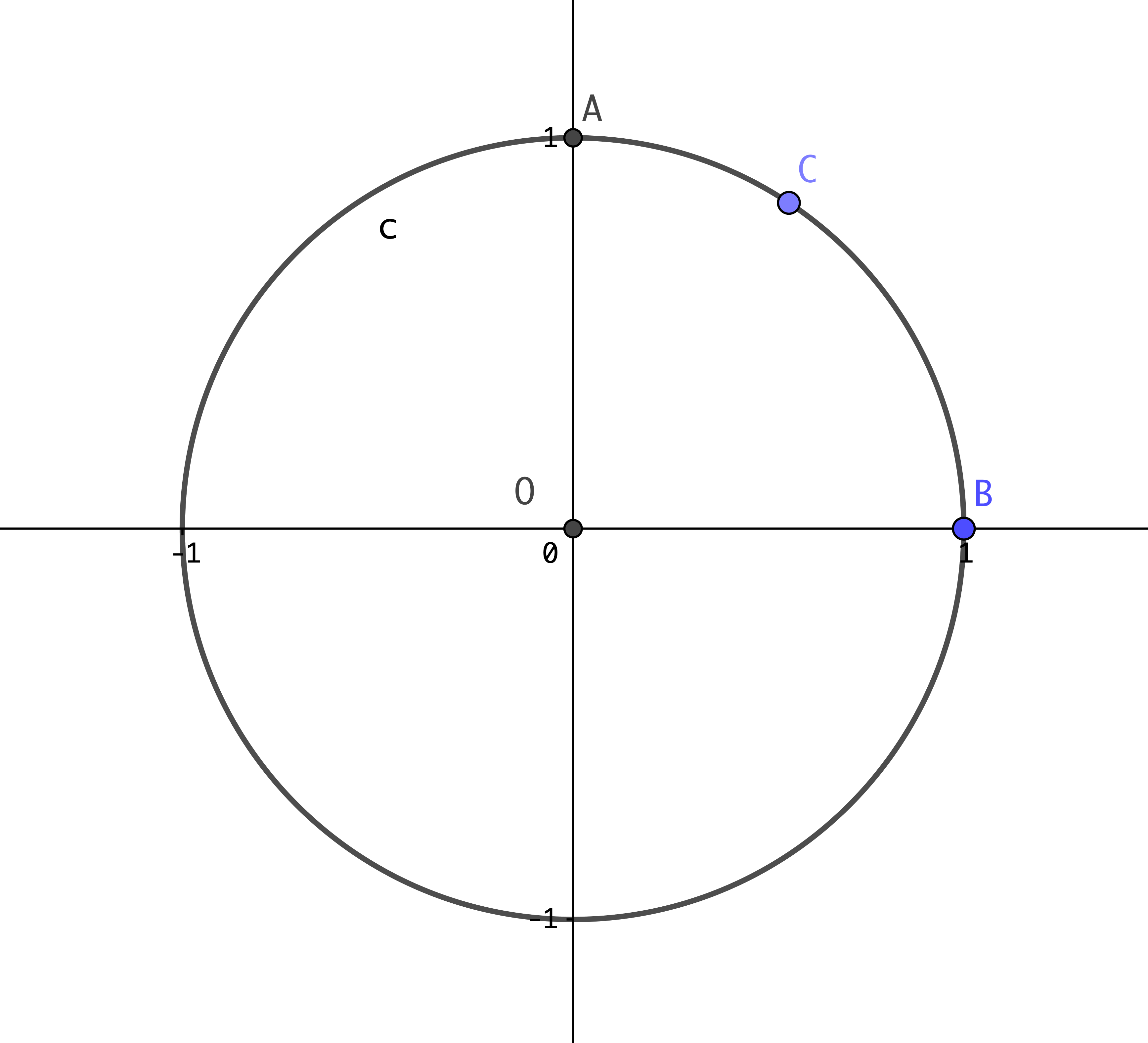

半径が1、中心が原点となっている円です。


この単位円上の2点A,Bの座標を求められるでしょうか?




では点Cの座標を求めてみてください。






そうですね、点Cの座標なんて分かるはずがありません。




そこで下の図のように、半径1であることと、\(\angle BOC\)に着目します。




するとここに斜辺が1、底辺がOD、高さがCDの直角三角形が出現します。
このとき
ポイント
\(CD=\sin\theta\)
\(OD=\cos\theta\)


と表します。


サインコサイン基本講座|サインコサインの2つの定義
この気持ちを理解した上で、サインコサインの2つの定義「三角比」「三角関数」を見てみましょう。
三角比の定義
三角比の定義
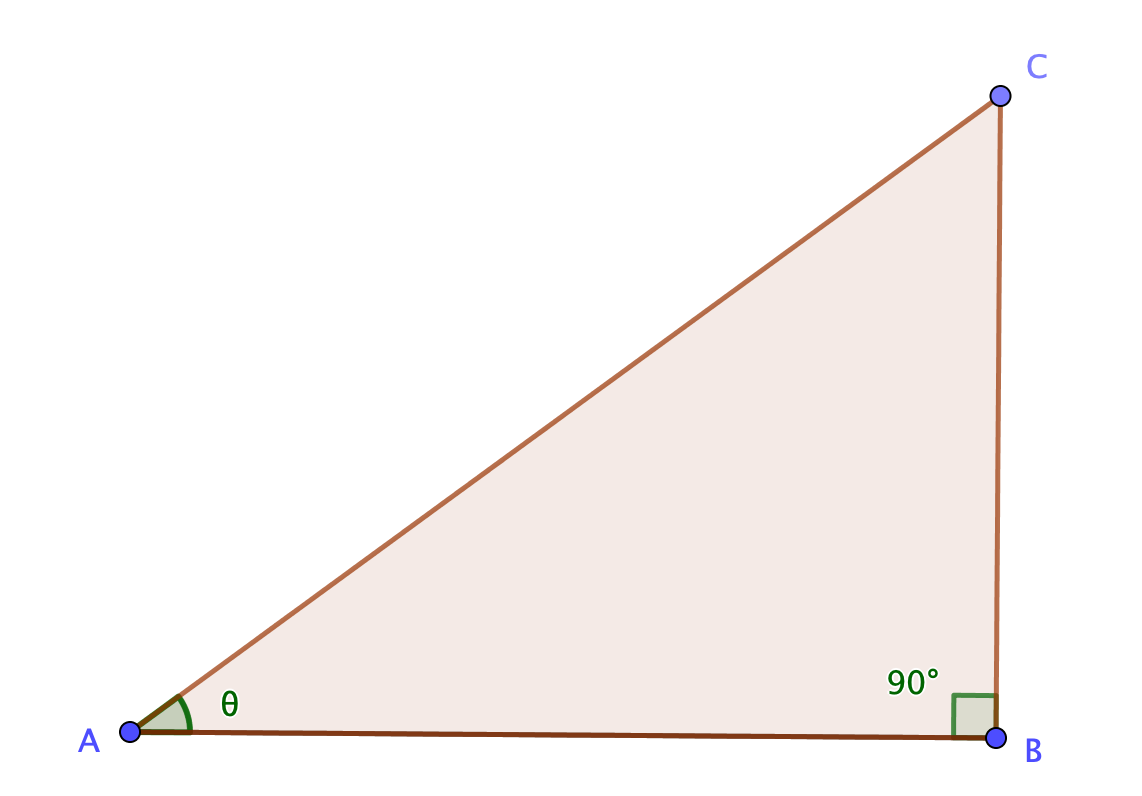

\(0<\theta<90^{\circ}\)のとき
$$\cos\theta=\frac{AB}{AC}$$
$$\sin\theta=\frac{BC}{AC}$$




中学校で習った相似の考え方で、3つの辺を全て同じ値で割っても三角形の形は変わりません(大きさは変わるけどね)。この相似の性質を利用して、\(AC,AB,BC\)の3辺を\(AC\)で割ることで、斜辺の長さが1の同じ形の三角形を考えることなります。
例
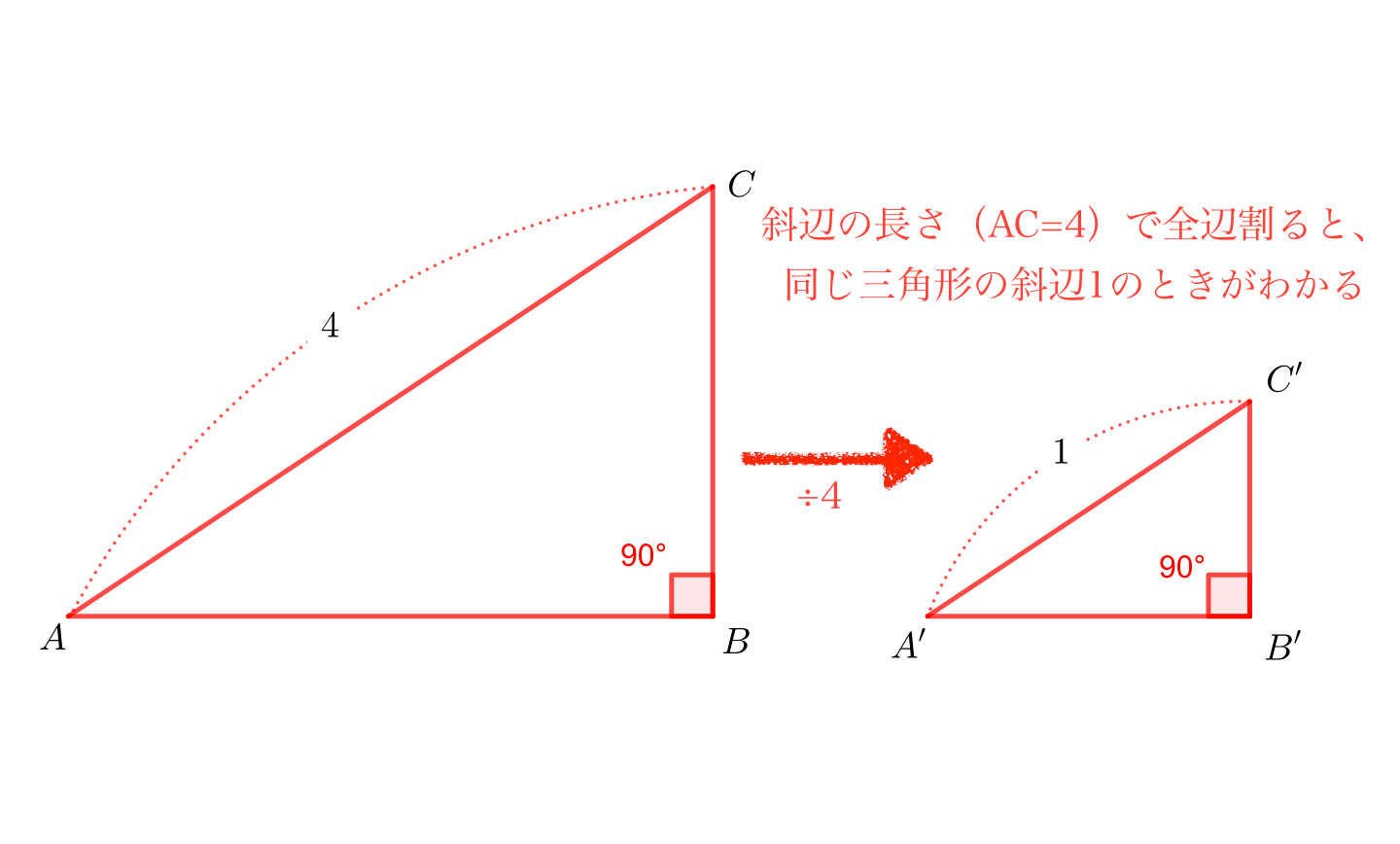

サインコサインの本質的な意味は、斜辺が1の直角三角形の高さと横幅。どうしても斜辺が1の直角三角形を作る必要があるわけですね。
三角関数の定義
三角関数の定義
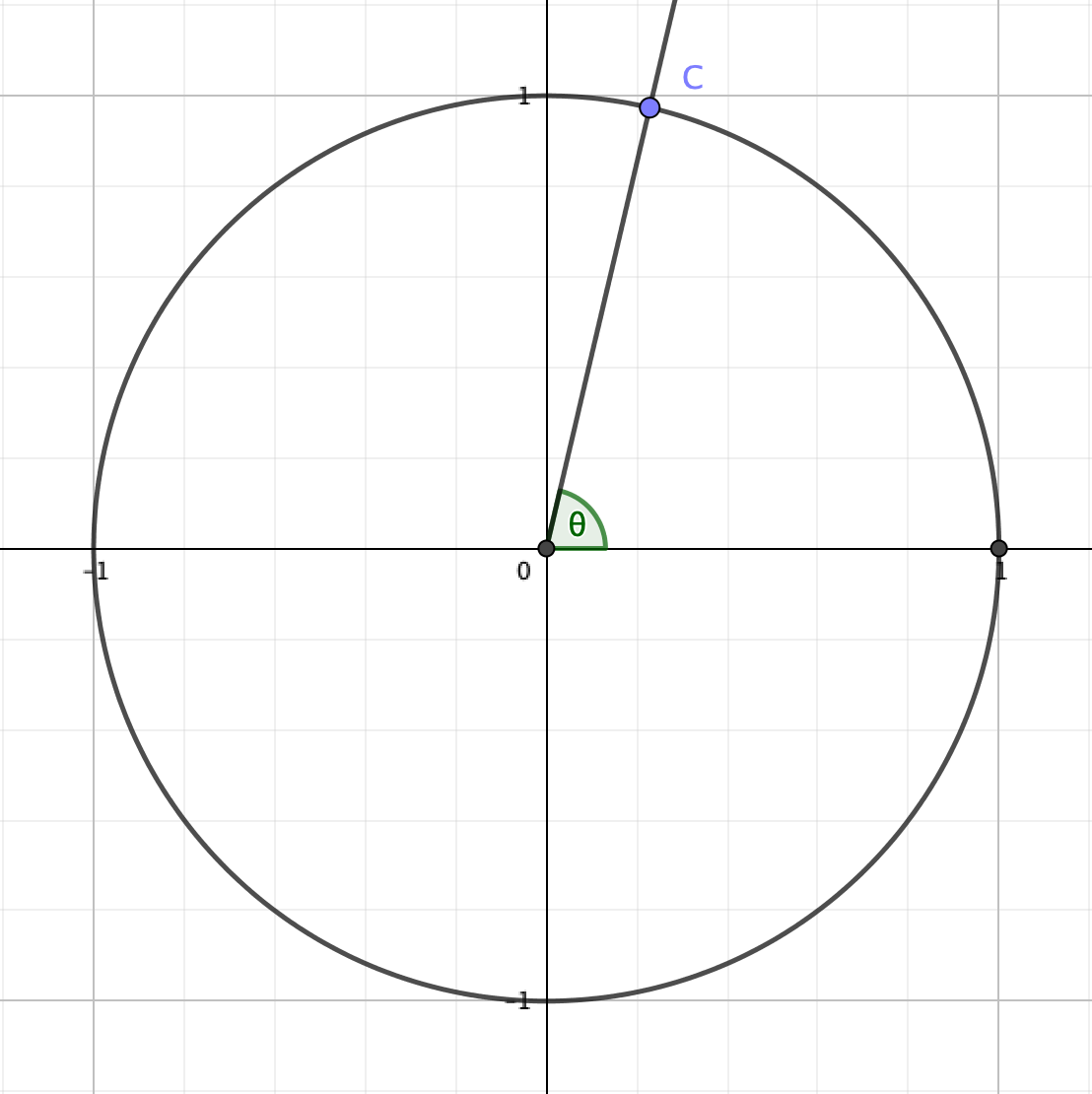

\(x\)軸の正の部分を原点中心に、反時計回りに\(\theta\)だけ回転させた半直線\(OC\)と、単位円の交点の座標を\((\cos\theta,\sin\theta)\)とする。




この定義における\(\theta\)は、点\(C\)が点\((1,0)\)を出発してできる半直線が作る角度ということになっています。
この点\((1,0)\)には、始点という名前がついています。
サインコサイン基本講座|【暗記は必要ない】サインコサインの値


サインコサインの定義がしっかり理解できたところで、皆さんが学校で無理やり覚えさせられるあの値について考えていきましょう。






実は先ほどの意味解説の場面でも、定義の場面でも必ず登場したキーワードがあります。
それは直角三角形です。




中でも値を求める上で重要なのは、三平方の定理を使って求められる有名三角形の比率です。
有名三角形の辺の比率①
【有名三角形①】


内角が\(90^{\circ},60^{\circ},30^{\circ}\)で構成されている直角三角形\(\triangle ABC\)の辺は、\(BC\)の長さが1のとき\(AC=2,AB=\sqrt{3}\)となる。
有名三角形の辺の比率②
【有名三角形②】


内角が\(90^{\circ},45^{\circ},45^{\circ}\)で構成されている直角二等辺三角形\(\triangle ABC\)の辺は、\(BC\)の長さが1のとき\(AC=\sqrt{2},AB=1\)となる。


そして、サインコサインの定義の中には、「直角であること」と同じくらい重要なポイントがあります。




有名三角形①の斜辺を1にするために、3つ全ての辺に\(\times\frac{1}{2}\)してみましょう。
すると高さが\(\frac{1}{2}\)、底辺が\(\frac{\sqrt{3}}{2}\)の直角三角形になりますね。
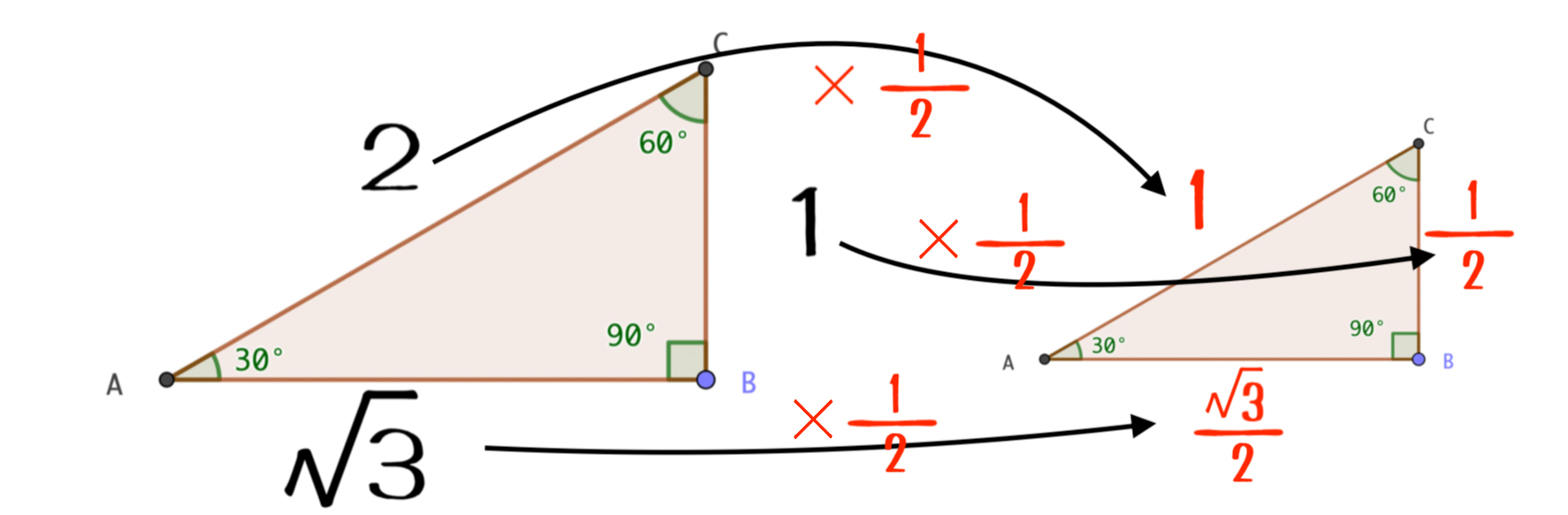

では、\(\sin30^\circ\)と\(\cos30^\circ\)が意味する場所を考えてみてください。(「サインは高さ、コサインは横幅」を意味するのでした。)
$$\Large{\cos30^\circ=AB=\frac{\sqrt{3}}{2}}$$
となりますね。






サインコサイン基本講座|【2秒で覚えられる】サインコサインの値一覧と覚え方
先ほど紹介した導出方法を用いると、以下の覚えさせられる値は簡単に導出できます。
| \(\theta\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | \(120^{\circ}\) | \(135^{\circ}\) | \(150^{\circ}\) | \(180^{\circ}\) |
| \(\sin\theta\) | \(0\) | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | \(0\) |
| \(\cos\theta\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | \(0\) | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) |
(見切れている場合はスクロール)




この表の値を1つずつ覚えてもいいのですが、表丸ごとワンセットで覚えてしまいましょう。
その覚え方というのは、\(\frac{\sqrt{○}}{2}\)の形で統一するという方法です。
実際、統一してみると・・・
| \(\theta\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | \(120^{\circ}\) | \(135^{\circ}\) | \(150^{\circ}\) | \(180^{\circ}\) |
| \(\sin\theta\) | \(\frac{\sqrt{0}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{0}}{2}\) |
| \(\cos\theta\) | \(\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{0}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{4}}{2}\) |
(見切れている場合はスクロール)
サインの分子のルートの中身は0→4→0の順に、コサインの分子のルートの中身は4→0→4の順になっていますね。


ちなみに、覚える値が\(0^{\circ}\)とか\(30^{\circ}\)のように決められているのは、三平方の定理で求めることができる角度だから。
\(\sin27^{\circ}\)とか言われても三平方の定理から求めることができないし、綺麗な値でもないのであまり有用性がないんですね。
サインコサイン基本講座|サインコサインの公式


サインコサインの値は、有名三角形2つの辺の比を元に導出することができました。
ですが直角三角形の重要定理、三平方の定理を満たすことも忘れてはいけません。
内角がどんな構成になっている直角三角形でも、三平方の定理は必ず成立します。
三平方の定理


どの直角三角形でも、\(BC^2+AB^2=AC^2\)を満たす。
つまり、サインコサインにこの考えを適用すると次の式が得られます。


図の\(\triangle ODC\)において、\(CD^2+OD^2=OB^2\)。
よって、\(\sin^2\theta+\cos^2\theta=1^2=1\)となるわけです。
ポイント
\(\sin^2\theta+\cos^2\theta=1\)
そのほかにサインコサインには
のように、大量に公式があります。
ただし、これらは全て覚えるというよりは、理解することが重要です。
それぞれの変形では何が意識されていて、何をするときに適用するのか。そう言ったことを意識してみるようにしてください。
サインコサイン基本講座|【いつ使う?】サインコサインの活用場面


サインコサインはこれまでみてきた通り、斜辺の長さ・底辺と斜辺がなす角\(\theta\)さえわかれば、直角三角形の底辺や高さが求められます。
これの恩恵を、数学的な場面でみてみましょう。
三角形の面積
三角形の面積を求める公式はご存知ですね?
そう、底辺\(\times\)高さ\(\div2\)です。
では、次の三角形の面積はどのように求められるでしょうか。
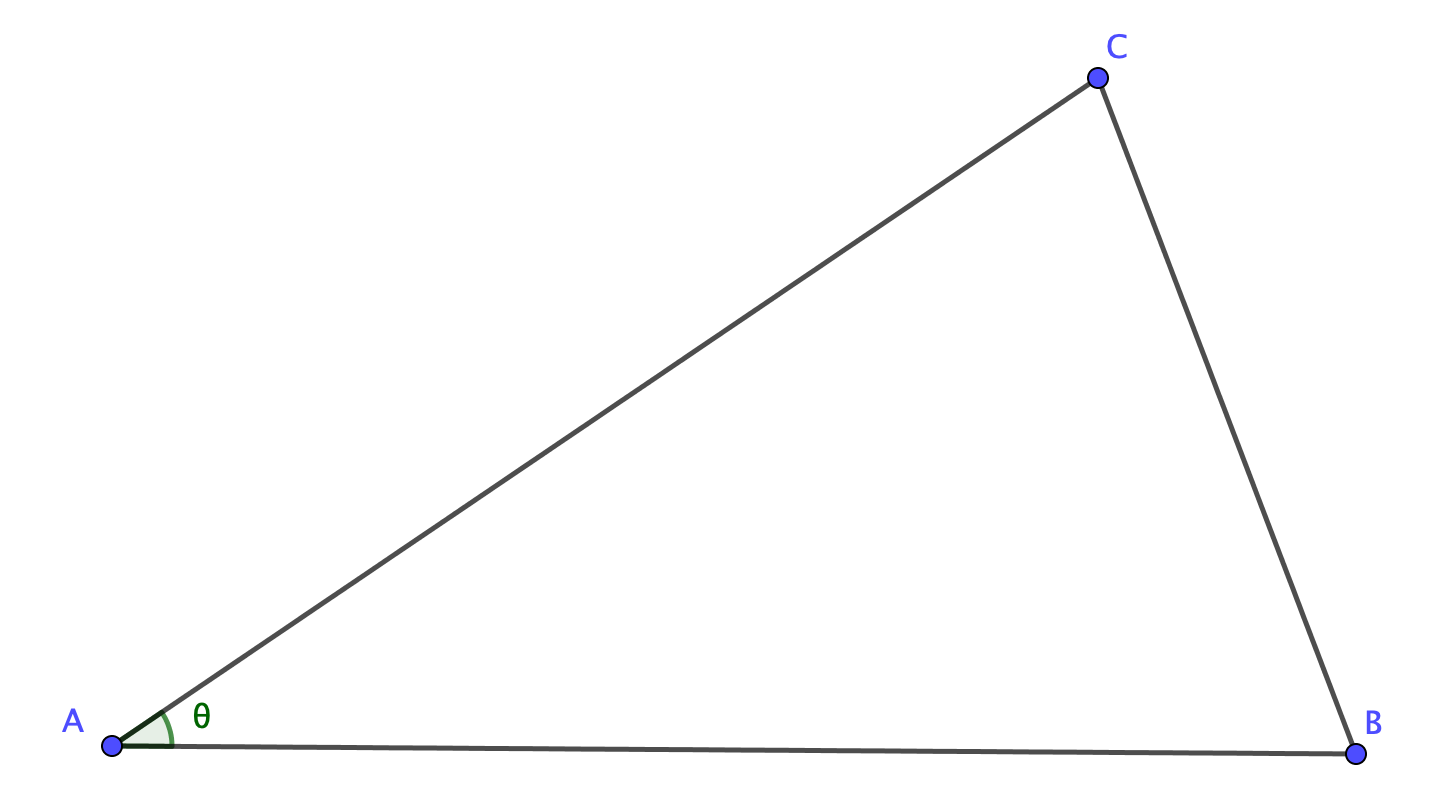





図のように、頂点から底辺に垂線\(CD\)を下ろしてみましょう。
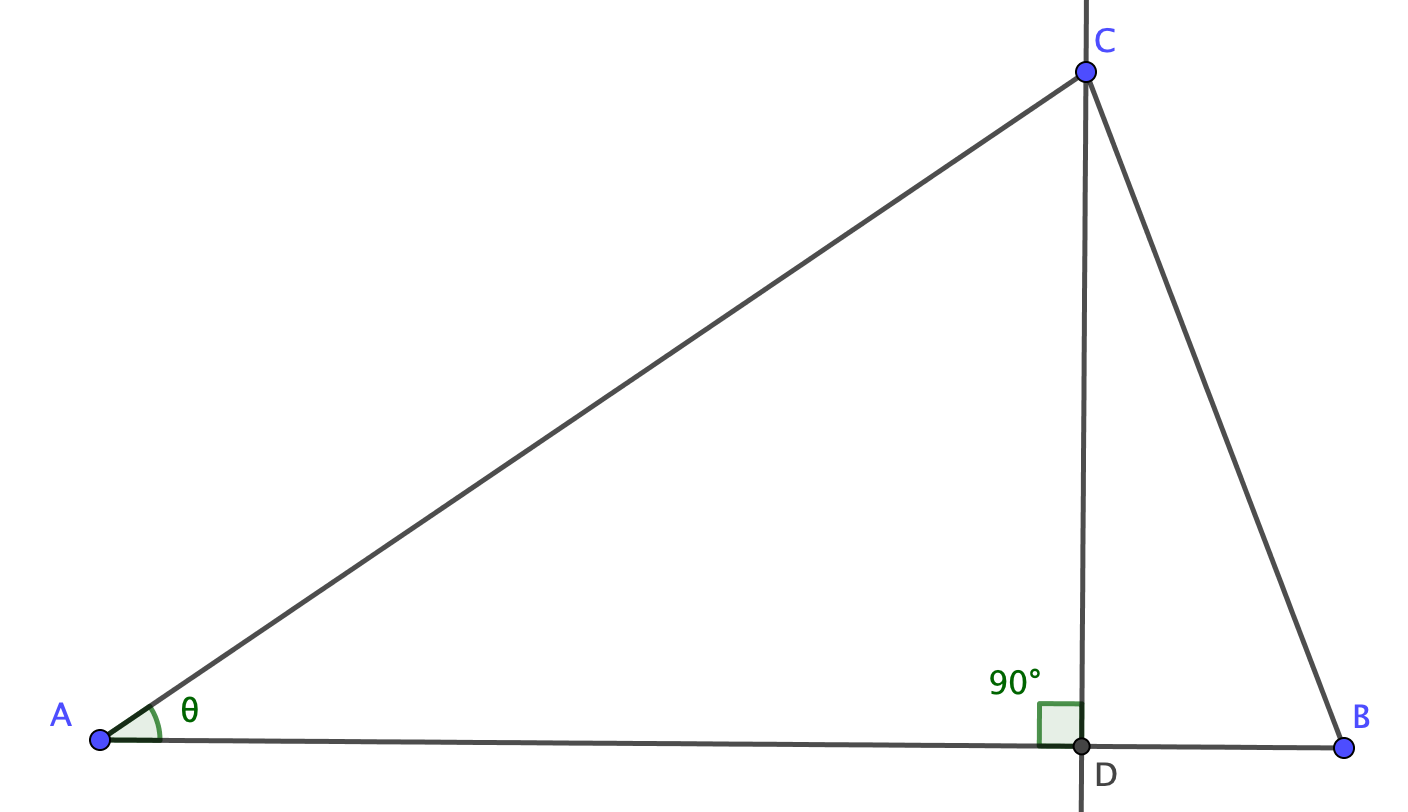

するとここに、2つの直角三角形\(\triangle ADC,\triangle BDC\)が登場します。
CDが高さに該当しますが、これまでの流れでお分かりの通り、
で求めることができます。






ポイント
よってどんな三角形の面積でも
$$三角形の面積=\frac{1}{2}\times AB \times AC\times\sin\theta$$
で求められることがわかります。


サインコサイン基本講座|まとめ


まとめ
- サインコサインは斜辺が1の直角三角形の高さと底辺のこと。
- サインコサインの値を求めるためには、有名三角形の比率を考えれば良い。
- サインの値を覚えるためには、ルートの中身は0→4→0の順にすれば良い。
- コサインの値を覚えるためには、ルートの中身は4→0→4の順にすれば良い。
- \(\sin^2\theta+\cos^2\theta=1\)など、いろんな場面に合わせた変形ができる。
サインコサインは、数学を学ぶ上でかなり大事な部分になってきます。公式を覚えるのではなく、理解してしっかり使えるようになってください。
今回のサインコサインの意味をしっかり押さえておけば、問題を解く際に「あれ、お前サインコサイン使うんじゃね?」的な感覚が働くようになりますよ!
以上、「サインコサイン基本講座」でした。









