【差がつくポイント】二項定理はイメージで覚えろ！重要なポイントと活用場面を総まとめ！

小春

楓くん、二項定理ってなんか複雑な式で覚えにくいんだけど。。。

えっ、あんなの覚えるもんじゃないよ！！

楓

小春

覚えなくていいの？

式よりもどういう意味が込められているかが大事だよ！今日は二項定理の気持ちをしっかり理解していこう。

楓

組み合わせと二項定理｜組み合わせの意味

まずは簡単に、組み合わせについて復習してみます。

この組み合わせは、順列との対応を理解することで意味が明確になりますよ。

例えば、順列では、1と2の数の並び\((1,2)(2,1)\)は別物としてカウントされます。

一方組み合わせは、この2つを全く同一のものとして扱います。

楓

要は数の順番を一方的に無視するという話です。

他にも順列では「左手にもつか、右手にもつか」を区別するような事象でも、組み合わせでは「手にもつ」という事象にまとめられたりもします。

このように順番やどちらの手に持つかなど、あらゆる区別を排除し、まとめたものが組み合わせの本質です。

順列と組み合わせの違いについて復習したい人はこちらを参考にしてください。

組み合わせと二項定理｜二項定理の意味

楓

ではまず、簡単な具体例から見ていきましょう。

次の展開公式を見てください。

この展開式では、\(xa+ax\)をあえてそのまま残してあります。

あなたはこれを\(2ax\)と書き直しますね？なぜ、そのように書き換えられるのでしょうか。

小春

そんなの当たり前じゃないの？？

そう、当たり前なんです。

今あなたが習っている数学のかけ算では交換法則が成り立ちます。

つまり\(a\times x\)と\(x\times a\)は区別されず、同じ値とみなせるんですね。

小春

だから組み合わせ\(_nC_r\)が登場するんだね。

ここで展開するときの考え方を復習してみましょう。

2つのカッコ\((x+a)(x+a)\)のうち、最初のカッコから\(x\)を選択したとします。

このとき、2つ目のカッコの中からは\(x\)を選ぶ方法と\(a\)を選ぶ方法の2通りが考えられますね。

次に1つ目のカッコから\(a\)を選択したとします。

このとき、2つ目のカッコの中からは先ほどと同じように、\(x\)を選ぶ方法と\(a\)を選ぶ方法の2通りが考えられますね。

このように展開とは、掛け合わされるすべてのカッコの中から1つ文字を選んでいく作業と見なせます。

この作業の中では\(ax\)と\(xa\)のように、文字の順番は区別されません。

では一般的に\((x+a)^n\)について考えてみましょう。まずは、

のようにn個の\((x+a)\)のかけ算に分けます。

この全てのカッコたちの中から1つずつ値を選んでいくという認識が重要です。

小春

全てっていうワードが特に重要なのね笑

例えばn個のカッコの中から\(x\)を2回だけ選ぶパターンを考えましょう。

すると、

のように複数の\(x\)と\(a\)のかけ算が登場します。

しかしかけ算の交換法則のおかげで、これらは全て\(a^{n-2}x^2\)と表せます。

ではこの\(a^{n-2}x^2\)となるパターンは何通り登場するのでしょうか。

\(n\)個のカッコの中から\(x\)を2回、\(a\)を\(n-2\)回選んで、その順番は区別しないので\(_nC_2\)通りですね。

\(_nC_2\)通り\(a^{n-2}x^2\)が登場する、すなわち\(_nC_2\)回\(a^{n-2}x^2\)を足すわけですから、それらすべてをまとめると\(_nC_2 a^{n-2}x^2\)となります。

\(_nC_2\)が\(a^{n-2}x^2\)の係数に一致することを考えると、

と表せることが納得できますね。

楓

要は係数の回数だけ、\(x^{〇}a^{n-○}\)が登場するってことね。

組み合わせと二項定理｜パスカルの三角形

二項定理を理解すると、それほど難しいことを言っているわけではないことに気がつきます。

でも、\((x+a)^2\)や\((x+a)^3\)といった展開式を考えるときに、いちいち二項定理を使いたくはありません。

小春

確かに指数が小さい時に、二項定理を使うとむしろ計算に手間取りそうだよね。

そう。二項定理は問題を解く際に、積極的に使いたくはない手法だよね。

楓

でも展開を普通にやるのも面白くないし、計算ミスもちょっと心配です。

そこでパスカルの三角形というものを活用しましょう。

パスカルの三角形とは、図のような側面に1を並べたピラミッドのこと。

中の数は、隣り合う2つの数の和で構成されています。

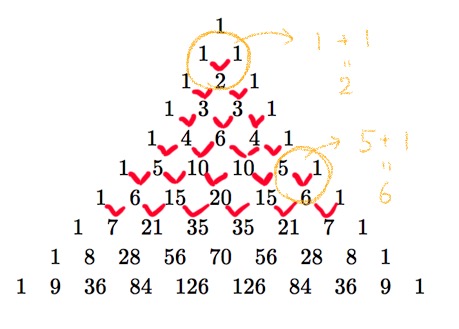
この三角形の凄いところは、頂点の1を0段目とすると、\(n\)段目の数の並びは\((x+a)^n\)の各項の係数と一致しているということです。

例えば2段目の『1 2 1』という数の並びは

と係数に一致しています。

3段目の『1 3 3 1』という数の並びは

となり、これも係数に一致しています。

楓

だから係数をサッと簡単に求めたい場合は、パスカルの三角形が有効だよ。

パスカルの三角形と二項定理はどっちが楽？

パスカルの三角形を使えば、とても簡単に係数を求めることができます。

しかし、例えば\((x+3)^{21}\)における\(x^7\)の係数を求めるのはしんどいんですよね・・・。

つまり

というように、場面に合わせて使い分けた方が良いです。

問題の場面に合わせて、適材適所で使ってみてください。

組み合わせと二項定理｜二項定理の具体的な問題

例題

$$\sum_{k=0}^{n} {_nC_k}$$

の値を求めよ。

---

（解答）

問題が複雑なので、とりあえずシグマを分解してみると、

\begin{align} \sum_{k=0}^{n} {_nC_k} &= {_nC_0}+{_nC_1}+\cdots +{_nC_n}\\\ &= _nC_n 1^n 1^0+_nC_1 1^1 1^{n-1}+\cdots +_nC_0 1^0 1^{n}\\\ &= (1+1)^n\\\ \end{align}

（※見切れている場合はスクロール）

となる。

ここで強引に、次のように考えてみる。

\begin{align} {_nC_0}+{_nC_1}+\cdots +{_nC_n} &= _nC_n 1^n 1^0+_nC_1 1^1 1^{n-1}+\cdots +_nC_0 1^0 1^{n}\\\ \end{align}

楓

二項定理が使えそうな形だなぁと思って変形しているよ！

よって、

\begin{align}  {_nC_0}+{_nC_1}+\cdots +{_nC_n} &= _nC_n 1^n 1^0+_nC_1 1^1 1^{n-1}+\cdots +_nC_0 1^0 1^{n}\\\ &= (1+1)^n\\\ \end{align}

楓

1. 複雑なので、わかりやすく分解
2. 二項定理に似た形なので、代入してみる

というプロセスが大事

特に2番目のプロセスは、二項定理を知らないと思いつかないから要注意だね。

小春

組み合わせと二項定理｜まとめ

楓

最後にまとめです。

二項定理は最初にも述べたとおり、問題として多くは出現しませんが重要な証明のキーを握る存在であることも多いです。

特にべき乗（〜乗された数）の計算ではかなり重要な立ち位置を占めており、微分公式の導出には必須の定理です。

テストや受験で油断している受験生と差をつけるポイントにもなりますので、ぜひ覚えておいてください。

以上、「二項定理の意味」についてでした。