加法定理の使い方とイメージしやすい証明→覚えることは２つだけ！

Today's Topic

$$\sin\left(\theta + \alpha \right) = \sin \theta \cos \alpha + \cos \theta \sin \alpha$$

$$\cos\left(\theta + \alpha \right) = \cos \theta \cos \alpha - \sin \theta \sin \alpha$$

楓

今日は、加法定理をやってみよう！

はあ、いよいよ加法定理かぁ・・・。覚えるの多いんだよねぇ？

小春

楓

覚えるのは2つで十分！他のは自分で簡単に導出できるよ！！

2つだけなの！？でも、何言っているかよくわかんないから、その2つも怪しそう・・・。

小春

楓

それなら今日は、加法定理の意味と使い方もじっくりみていこう！

こんなあなたへ

「加法定理が覚えられない！」

「加法定理って何言ってるの？何の役に立つの？」

この記事を読むと、こんな問題が解ける！

$ \cos\left(75^\circ\right) = \frac{\sqrt{6} + \sqrt{2}}{4}$
$\sin\left(\theta+30^\circ\right)+2\cos\theta$を$\sin\theta ,\cos\theta$のみで表せ。

答えは一番最後にあるよ！

楓

三角関数を一気に理解したい方への記事は、こちらにまとめてあります。

まとめ記事

: 【三角関数基礎まとめ】暗記0のサインコサイン！本質から使い道まで徹底解説

続きを見る

Contents

1 加法定理とその解説
2 加法定理の覚え方
3 【図形でわかる3ステップ】加法定理の証明
4 加法定理の使い方
- 4.1 加法定理の使い方①｜有名角以外のサインコサインの値がわかる
- 4.2 加法定理の使い方②｜新たな公式が導ける
5 まとめ

加法定理とその解説

加法定理とは以下６つの公式のことを言い、今回はサインコサインの加法定理にフォーカスしたテーマで書いていきます。

というのも、後述しますが、タンジェントの公式は基本的に自分で求めた方が楽だからです。

加法定理

$$\sin\left(\theta + \alpha \right) = \sin \theta \cos \alpha + \cos \theta \sin \alpha$$
$$\cos\left(\theta + \alpha \right) = \cos \theta \cos \alpha - \sin \theta \sin \alpha$$
$$\sin\left(\theta - \alpha \right) = \sin \theta \cos \alpha - \cos \theta \sin \alpha$$
$$\cos\left(\theta - \alpha \right) = \cos \theta \cos \alpha + \sin \theta \sin \alpha$$
$$\tan\left(\theta + \alpha \right) = \frac{\tan\theta+\tan\alpha}{1-\tan\theta\tan\alpha}$$
$$\tan\left(\theta - \alpha \right) = \frac{\tan\theta-\tan\alpha}{1+\tan\theta\tan\alpha}$$

（※見切れている場合はスクロール）

最初の２つさえ覚えておけば、他の公式は自分で導くことができます。

例えば、3つ目の$\sin \left(\theta - \alpha\right)$は、最初の$\sin \left(\theta + \alpha\right)$の$\alpha$を$-\alpha$に書き換えてあげればOK。

式変形の際は、

$$\sin \left(-\alpha\right)=-\sin\alpha$$
$$\cos \left(-\alpha\right)=\cos\alpha$$

に注意しましょう。

実際にやってみると、

\begin{align} \sin\left(\theta + \left(-\alpha\right)\right) &= \sin\theta\cos\left(-\alpha\right)+\cos\theta\color{red}{\sin\left(-\alpha\right)}\\\ &= \sin \theta \cos \alpha \color{red}{-} \cos \theta \color{red}{\sin \alpha}\\\ \end{align}

（※見切れている場合はスクロール）

となります。

タンジェントについては、

$$\tan \theta = \frac{\sin \theta}{\cos \theta}$$

を利用して

$$\tan \left(\theta+\alpha\right) = \frac{\sin \left(\theta+\alpha\right) }{\cos \left(\theta+\alpha\right) }$$

で求めることができます。

楓

僕はタンジェント公式は一切覚えず、必要な時に導出するスタンスがオススメ！

実はこのときポイントがあって、$\cos\theta\cos\alpha$で分母分子を割るとうまくいきます。

\begin{align} \tan \left(\theta+\alpha\right) &= \frac{\sin \left(\theta+\alpha\right) }{\cos \left(\theta+\alpha\right) }\\\ &= \frac{\sin \theta \cos \alpha + \cos \theta \sin \alpha}{\cos \theta \cos \alpha - \sin \theta \sin \alpha}\\\ &=\frac{\frac{\sin \theta \cos \alpha + \cos \theta \sin \alpha}{\color{red}{\cos\theta\cos\alpha}}}{\frac{\cos \theta \cos \alpha - \sin \theta \sin \alpha}{\color{red}{\cos\theta\cos\alpha}}}\\\ &= \frac{\tan\theta+\tan\alpha}{1-\tan\theta\tan\alpha}\\\ \end{align}

以上のことから、最初の2つさえ証明できてしまえばあとは式変形で難なく突破できます。

ではその証明とは、どのようなものなのか。

ここではあまり複雑なものではなく、超絶分かりやすい証明を、後ほどご紹介します。結論から述べると、斜辺の長さに注意して高さと横幅の長さを求めるだけです！

加法定理の覚え方

証明に入る前に、覚え方について話しておきましょう。

加法定理はすでに述べたように、最初の２つ

$$\sin\left(\theta + \alpha \right) = \sin \theta \cos \alpha + \cos \theta \sin \alpha$$
$$\cos\left(\theta + \alpha \right) = \cos \theta \cos \alpha - \sin \theta \sin \alpha$$

だけ覚えられたら、あとは自分で求めた方が確実で、安心です。

よく「コスコス咲いた〜」みたいな暗記文句を聞くのですが、僕はこれで覚えられませんでした。

楓

ちなみに人間は、この脈絡のない言葉を覚えるのが苦手。言葉同士に意味や繋がりがないとなかなか脳は覚えてくれないよ。

どうせ覚えるなら効率よく覚えたいよね・・・。

小春

ここでは加法定理の２つの特徴に着目してみます。

①サインは＋のとき、右辺が＋。コサインは＋のとき、右辺ーになっている。

$$\sin\left(\theta \color{red}{+} \alpha \right) = \sin \theta \cos \alpha \color{red}{+} \cos \theta \sin \alpha$$
$$\cos\left(\theta \color{red}{+} \alpha \right) = \cos \theta \cos \alpha \color{red}{-} \sin \theta \sin \alpha$$

②サインはサインコサイン交互に、コサインはコサインコサイン、サインサインの形になっている。

$$\sin\left(\theta + \alpha \right) = \color{red}{\sin }\theta \color{red}{\cos }\alpha +\color{red}{\cos }\theta \color{red}{\sin } \alpha$$
$$\cos\left(\theta + \alpha \right) = \color{red}{\cos } \theta \color{red}{\cos } \alpha -\color{red}{\sin }\theta \color{red}{\sin } \alpha$$

なので僕はいつも、

$$S = SC+CS$$
$$C = CC- SS$$

と覚えていました。

楓

これ慣れるとパパって出るからオススメ。

【図形でわかる3ステップ】加法定理の証明

楓

サインコサインといったら単位円！

まずは単位円周上に2つの点A,Bをとります。

点Aは始点から$\theta$だけポイントにあり、点Bはその点Aから、さらに$\alpha$だけ進んだ位置にいます。

楓

点A,Bから下ろした垂線と$x$軸との交点をP,Qとします。

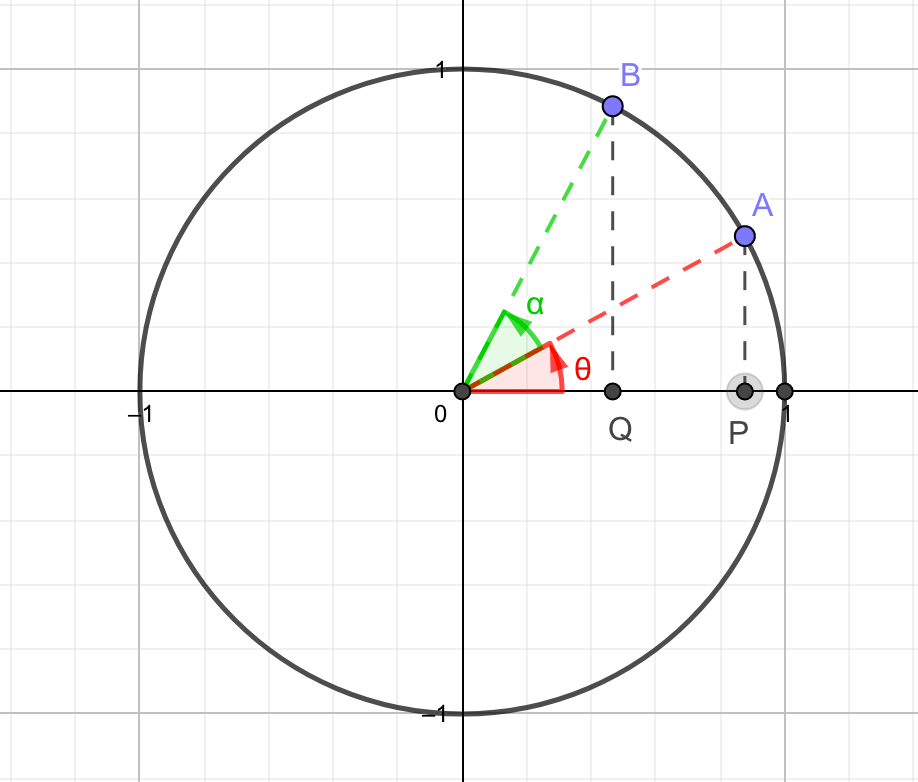
サインコサインの定義を簡単に復習すると、斜辺が1の直角三角形において、縦の長さを$\sin\theta$、横の長さを$\cos\theta$と表すのでした。

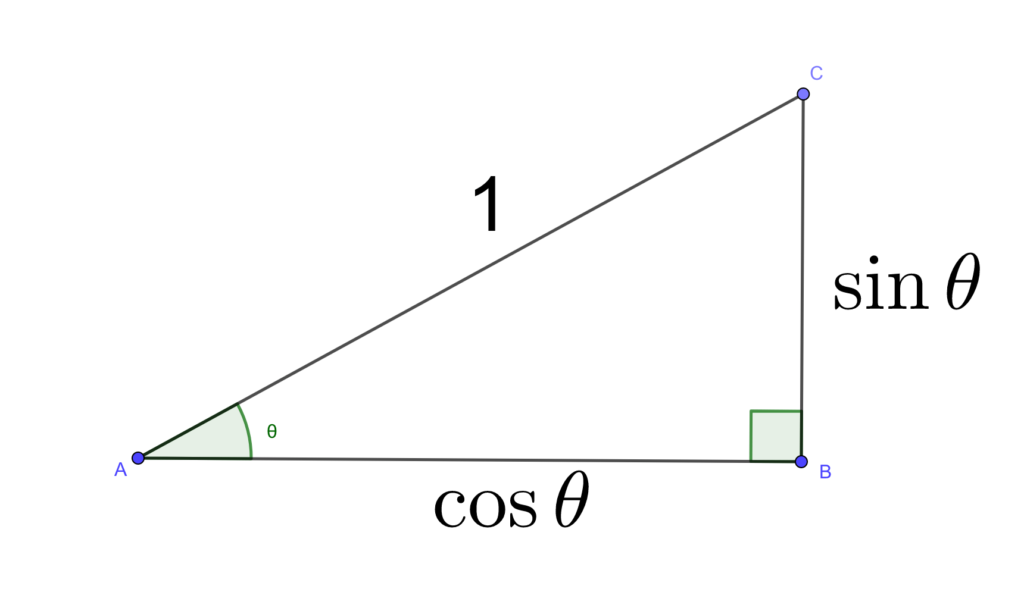
サインコサインの基本について復習したい人はこちらを参考にしてください。

: 【中学生でもわかった】サインコサインとは？公式を暗記しなくても、感覚でわかる！

続きを見る

つまり今回証明したい2つは、図と次のように対応づけられます。

$$\sin\left(\theta + \alpha \right) =BQ$$
$$\cos\left(\theta + \alpha \right) = OQ$$

楓

$OB=1$というところがポイントね！

では図で登場した2つの三角形に着目してみましょう。

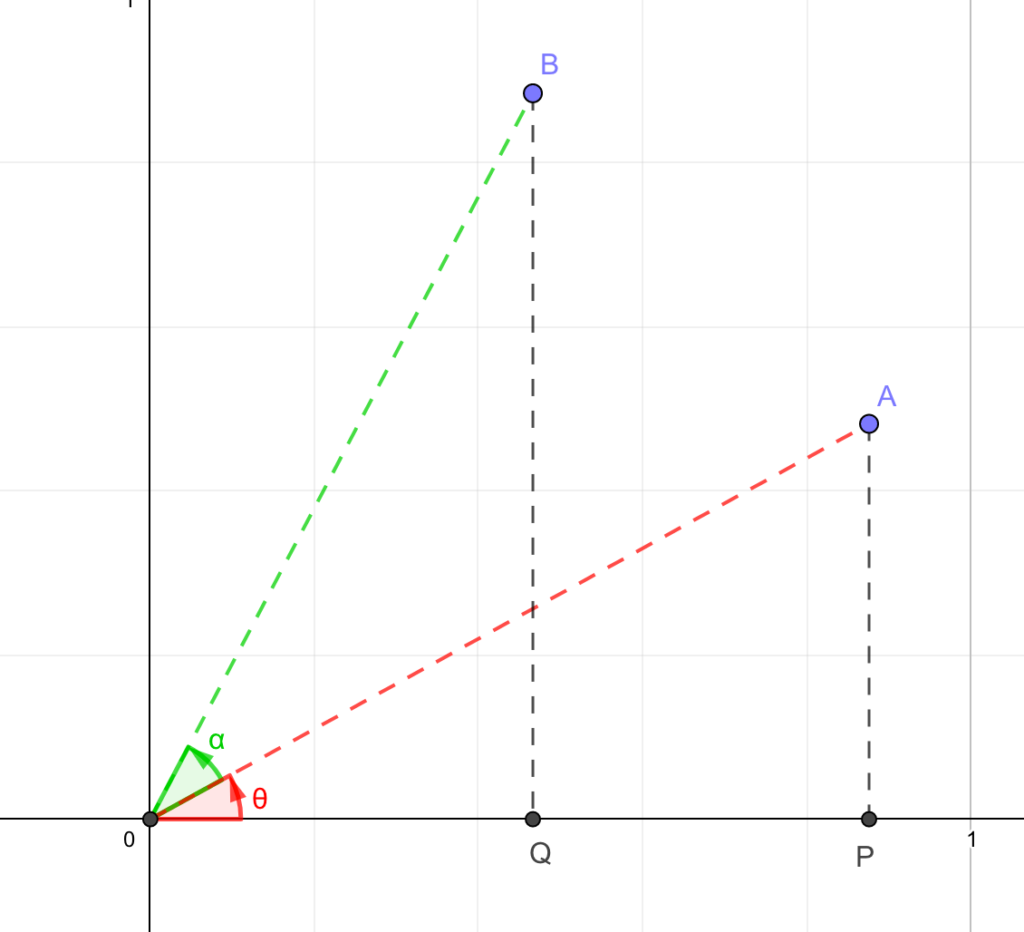
この図に、3点X,Y,Zを次のように定めます。

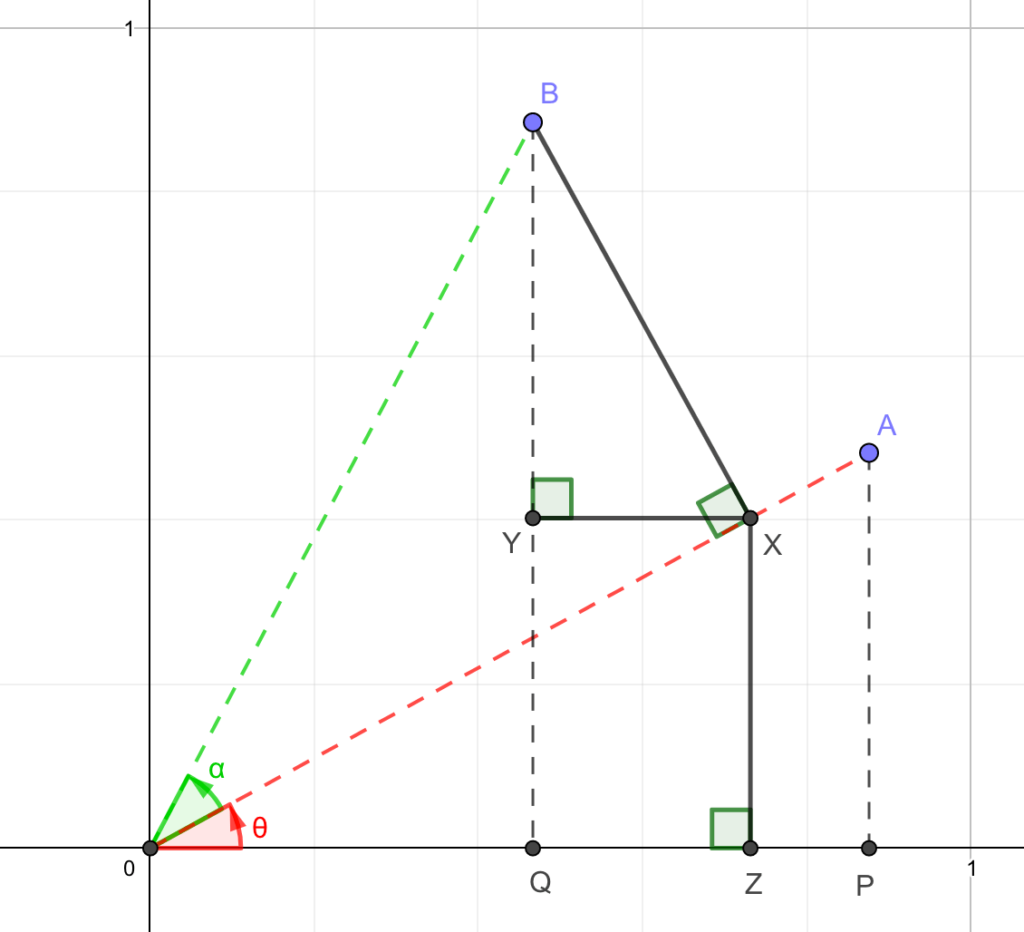
X・・・点BからOAに下ろした垂線の足
Y・・・点XからQBに下ろした垂線の足
Z・・・点Xから$x$軸に下ろした垂線の足

すると、今回求めたい長さQB,OQは、次のように求められそうです。

$$QB = QY + YB$$
$$OQ = OZ - ZQ$$

ではここから3つのステップに分けて求めていきましょう。

step
1QY、OZを求めよう。

$\triangle OXB$に着目してみましょう。

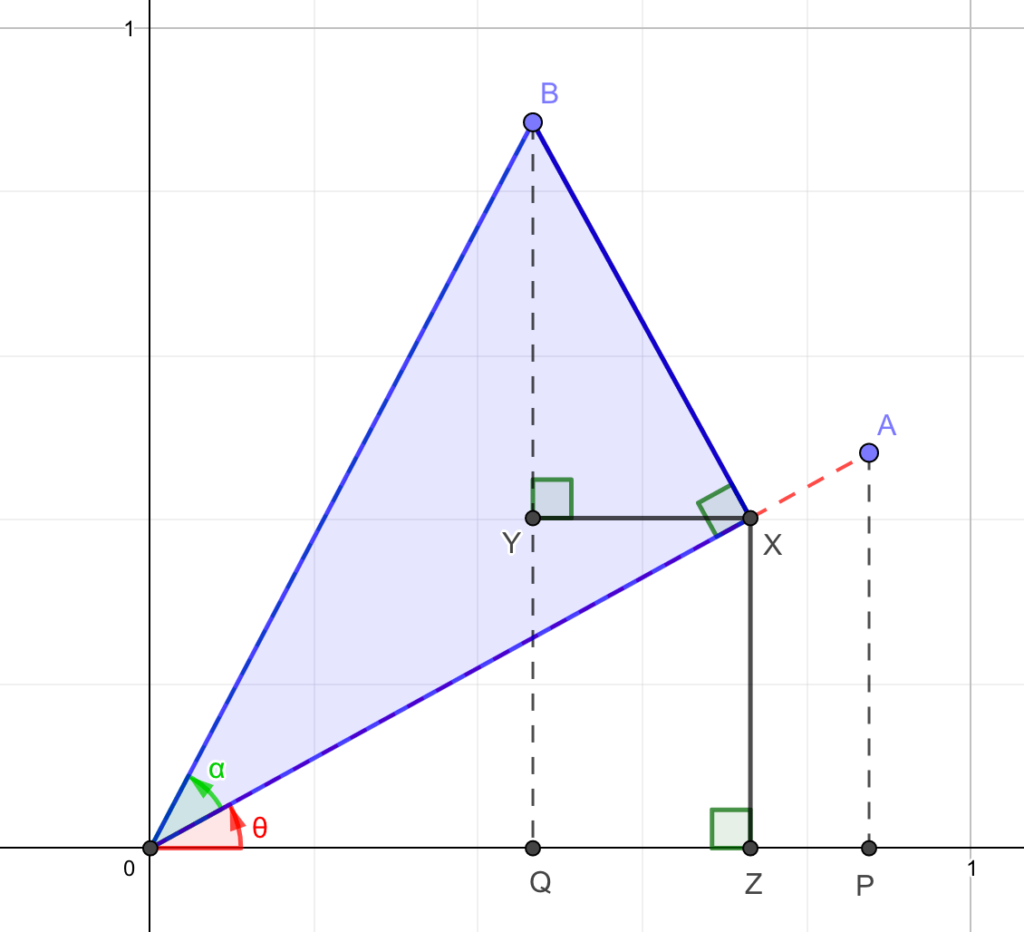
$OB=1$だったので、サインコサインの定義から

$$OX = \cos \alpha$$
$$BX = \sin \alpha$$

であることがわかります。

次に$\triangle OXZ$と$\triangle OAP$に着目しましょう。

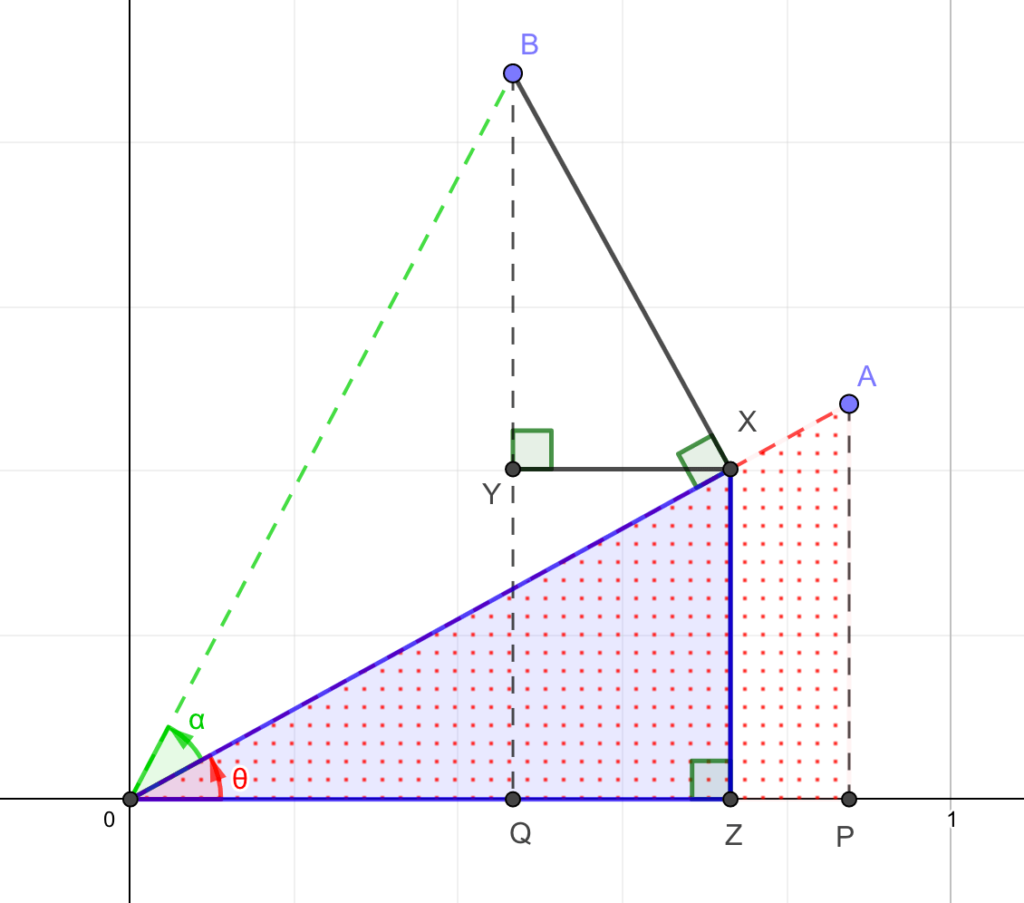
$\triangle OAP$は斜辺が1なのでサインコサインの定義から

$$OP = \cos \theta$$
$$AP = \sin \theta$$

と表せます。

一方、$\triangle OXZ$は斜辺の長さが$OX = \cos\alpha$なので、$XZ,OZ$は相似の関係から

$$OA : AP = OX : XZ$$
$$OA : OP = OX : OZ$$

で求める必要があります。

この比例式を計算すると、

\begin{align} XZ &= \frac{OX\times AP}{OA}\\\ &= \cos\alpha \sin \theta\\\ \end{align}
\begin{align} OZ &= \frac{OX\times OP}{OA}\\\ &= \cos\alpha \cos \theta\\\ \end{align}

となります。

楓

要は、$AP,OP$の長さを$OX$倍してあげると$XZ,OZ$が求められるってこと！

図から、$XZ = YQ$とわかるので

$$QY=\cos\alpha \sin \theta$$
$$OZ=\cos\alpha \cos \theta$$

となりました。

step
2YB、ZQを求めよう。

お次は$\triangle BXY$に着目します。

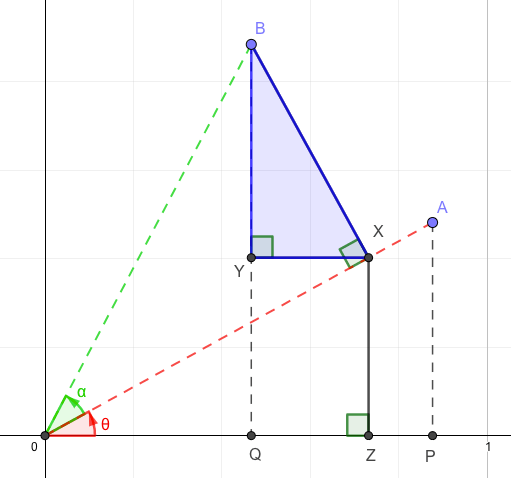
錯角が等しいことを利用すると

\begin{align} \angle BXY &= 90^\circ -\angle OXY\\\ &= 90^\circ - \theta\\\ \end{align}

とわかるので、変換公式に注意すると、

$$YB = \sin \left(90^\circ - \theta\right)=\cos \theta$$
$$XY = \cos \left(90^\circ - \theta\right)=\sin\theta$$

となりそうです。

変換公式について復習したい人はこちらを参考にしてください。

: 【忘れても大丈夫！】サインコサインの変換公式、覚え方とコツ→単位円を描こう！

続きを見る

楓

ここで注意ポイント！

ふ、ふぇ！！？

小春

高さがサイン、横幅がコサインとなるのはあくまで斜辺が1の直角三角形においてです。

今回考えている$\triangle BXY$は、斜辺の長さが$XB=\sin\alpha$となっています。

よって、相似の関係から

$$YB = \color{red}{XB \times} \cos \theta = \color{red}{\sin\alpha}\cos\theta$$
$$XY = \color{red}{XB \times} \sin \theta = \color{red}{\sin\alpha}\sin\theta$$

というように、$XB$倍するのを忘れないようにしてください。

最後に図から$XY = ZQ$とわかるので、

$$YB = \sin\alpha\cos\theta$$
$$ZQ = \sin\alpha\sin\theta$$

step
3【答え】QB、OQを求めよう。

このステップはおまけです。

求めたかったのは$QB,OQ$でした。

$$QB = QY + YB$$
$$OQ = OZ - ZQ$$

を計算してみましょう。

ステップ1、ステップ2で求めた値を使うと

\begin{align} QB &= QY + YB \\\ &= \sin\theta\cos\alpha + \sin\alpha\cos\theta\\\ \end{align}
\begin{align} OQ &= OZ - ZQ \\\ &= \cos\theta\cos\alpha + \sin\alpha\sin\theta\\\ \end{align}

となります。

$$QB=\sin\left(\theta + \alpha\right)$$
$$OQ=\cos\left(\theta + \alpha\right)$$

だったので、

加法定理

$$\sin\left(\theta + \alpha\right) = \sin\theta\cos\alpha + \sin\alpha\cos\theta$$

$$\cos\left(\theta + \alpha\right) = \cos\theta\cos\alpha - \sin\alpha\sin\theta$$

が証明できました。

楓

お疲れ〜

長かったけど、要はサインコサインと斜辺の長さに注意して、縦の長さと横の長さを求めただけだね。

小春

加法定理の使い方

それではここから、加法定理が有用な具体的な問題場面を３つみていきましょう。

加法定理の使い方①｜有名角以外のサインコサインの値がわかる

$30^\circ$や$60^\circ$などサインコサインの値が簡単に求められる角を有名角と言います。

まず１つ目の場面としてご紹介する問題は、この有名角以外の角におけるサインコサインの値を求めるのに使うことができるパターンです。

楓

もちろん加法定理じゃ求められないものもあるよ。$27.3^\circ$とかね。

結論から述べると、加法定理が使える場面は、有名角以外の角が有名角同士の足し算引き算で求められる場面です。

例えば、$\sin 15^\circ$の値を求めてみましょう。

$$15^\circ = 45^\circ - 30^\circ$$

と有名角同士の引き算で表すことができるので、加法定理が使えます。

\begin{align} \sin 15^\circ &= \sin \left(45^\circ - 30^\circ\right)\\\ &= \sin45^\circ \cos 30^\circ -\cos45^\circ \sin30^\circ\\\ &= \frac{\sqrt{6}}{4} -\frac{\sqrt{2}}{4}\\\ \end{align}

（※見切れている場合はスクロール）

ポイント

有名角以外の角におけるサインコサインの値を求めるためには、

その角が有名角同士の加法減法で表せることに着目して、

加法定理を用いれば良い。

加法定理の使い方②｜新たな公式が導ける

加法定理は、2倍角の公式や積和の公式といった、新たな公式を導くことができます。

導かれた公式は多くのことを解明してくれるので、まさに加法定理はサインコサイン界の宝ともいうべき存在です。

ここでは軽く2倍角の公式を証明して、詳しくは別記事で紹介したいと思います。

2倍角の公式

$$\sin 2\theta = 2\sin \theta \cos \theta$$

証明

加法定理より、$\sin \left(\theta + \theta\right)$について考える。
\begin{align} \sin \left(\theta + \theta\right) &= \sin\theta\cos\theta + \cos\theta\sin\theta\\\ &= 2\sin\theta\cos\theta\\\ \end{align}

2倍角の公式、積和の公式について勉強したい人はこちらを参考にしてください。

: 【確実に解が求まる】2倍角の公式の効率的な覚え方→『加法定理＋ナニカ』

続きを見る

まとめ

最後にまとめをしておきましょう。

まとめ

加法定理は
$$\sin\left(\theta + \alpha \right) = \sin \theta \cos \alpha + \cos \theta \sin \alpha$$
$$\cos\left(\theta + \alpha \right) = \cos \theta \cos \alpha - \sin \theta \sin \alpha$$

（※見切れている場合はスクロール）
だけ覚えれば良い。
証明をするためには、斜辺の長さに注意して、直角三角形の幅と高さを求めれば良い。
有名角以外の角に対するサインコサインを求めるときに使えることがある。
加法定理は、他の公式を導くサインコサイン界の宝

加法定理はその重要性と使いやすさから、入試でよく出る変形の１つに必ず挙げられます。

今回はなるべく優しい言葉で書いたので長くなってしまいましたが、理解できるようになれば何も難しいことは言っていないと気づくはず。

加法定理にある程度慣れたら、2倍角や半角など、新しい公式に手をつけていきましょう！

以上、「加法定理　徹底攻略」でした。

最初の答え

\begin{align} \cos\left(75^\circ\right) &= \cos\left(45^\circ + 30^\circ\right)\\\ &=\cos45^\circ \cos 30^\circ - \sin45^\circ \sin 30^\circ \\\ &=\frac{\sqrt{6} + \sqrt{2}}{4} \\\ \end{align}

（※見切れている場合はスクロール）

$$\begin{align} \sin\left(\theta+30^\circ\right)+2\cos\theta &= \left(\sin\theta\cos 30^\circ + \cos \theta \sin 30^\circ\right) +2\cos\theta\\\ &= \frac{\sqrt{3}}{2}\sin\theta+ \frac{5}{2}\cos\theta\\\ \end{align}$$

（※見切れている場合はスクロール）

加法定理の使い方とイメージしやすい証明→覚えることは２つだけ！

【三角関数基礎まとめ】暗記0のサインコサイン！本質から使い道まで徹底解説

加法定理とその解説

加法定理の覚え方

【図形でわかる3ステップ】加法定理の証明

【中学生でもわかった】サインコサインとは？公式を暗記しなくても、感覚でわかる！

【忘れても大丈夫！】サインコサインの変換公式、覚え方とコツ→単位円を描こう！

加法定理の使い方

加法定理の使い方①｜有名角以外のサインコサインの値がわかる

加法定理の使い方②｜新たな公式が導ける

【確実に解が求まる】2倍角の公式の効率的な覚え方→『加法定理＋ナニカ』

まとめ

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則