Today's Topic
$$\sin^2\frac{\theta}{2} = \frac{1-\cos\theta}{2}$$
$$\cos^2\frac{\theta}{2} = \frac{1+\cos\theta}{2}$$
$$\tan^2\frac{\theta}{2} = \frac{1-\cos\theta}{1+\cos\theta}$$




こんなあなたへ
「半角の公式の覚え方や、使う場面が知りたい!」
「使うときのコツを教えて欲しい!」
この記事を読むと、この意味がわかる!
- \(\cos 15^\circ\)の値を求めよ。
- \(\int \cos^2 x \ dx\)の値を求めよ。


三角関数を一気に理解したい方への記事は、こちらにまとめてあります。
Contents
半角の公式|一覧
半角の公式は、以下3つのことを言います。
半角の公式
$$\sin^2\frac{\theta}{2} = \frac{1-\cos\theta}{2}$$
$$\cos^2\frac{\theta}{2} = \frac{1+\cos\theta}{2}$$
$$\tan^2\frac{\theta}{2} = \frac{1-\cos\theta}{1+\cos\theta}$$
(いつも言うことですが、)タンジェントは
を使って、必要な時に求めた方が負担が少なく、便利です。
半角の公式|証明
半角の公式は2倍角の公式から求めます。
2倍角の公式について復習したい人はこちらを参考にしてください。
続きを見る



【確実に解が求まる】2倍角の公式の効率的な覚え方→『加法定理+ナニカ』
2倍角の公式の
を\(\sin^2\theta\)について解くと、
が得られます。
\(\theta\)を\(\frac{\theta}{2}\)に書き換えてあげれば、半角の公式になります。
2倍角の公式の\(\cos2\theta\)の別の形
を利用して、\(\cos^2\theta\)について解くと、
が得られます。
こちらも同様に、\(\theta\)を\(\frac{\theta}{2}\)に書き換えてあげれば、半角の公式になります。
タンジェントの場合は、
と計算してあげて、\(\theta\)を\(\frac{\theta}{2}\)に書き換えてあげれば、
となります。




半角の公式|覚え方
半角の公式は
$$\sin^2\theta = \frac{1-\cos2\theta}{2}$$
のように\(\frac{\theta}{2}\)で書くこともあれば、\(\theta\)で書くこともあります。
僕個人としては後者の方を覚えることをオススメします。
2倍角から簡単に導出できますし、問題で利用する際には後者の方が使いやすいです。


またサインの場合、『シンジくん、2階に引っ越す』で覚えられます。




コサインの場合はーを+に書き換え、タンジェントは導出すれば難しくありません。
もし2倍角も忘れてしまった場合は、加法定理から導けばいいでしょう。
導出のポイント
- 加法定理+『\(\sin^2\theta+\cos^2\theta = 1\)』=2倍角の公式
- 2倍角の公式+『\(\sin^2\theta\)、もしくは\(\cos^2\theta\)に着目して書き換え』=半角の公式


半角の公式|使える場面と、使うコツ
半角の公式を使うタイミングは主に2つしかありません。
半角の公式を使うといいポイント
- 中途半端な角のサインコサインを求めたいとき
- 次数を下げたいとき
それぞれ具体的に見ていきましょう。
中途半端な角のサインコサインを求めるとき
例題
\(\cos 15^\circ\)の値を求めよ。
\(\cos15^\circ = \cos \frac{30^\circ}{2}\)であることに着目して、半角の公式を適用します。
着目ポイント
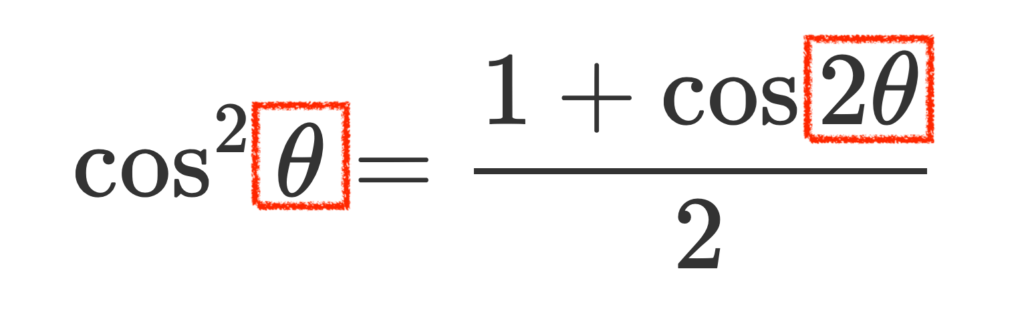
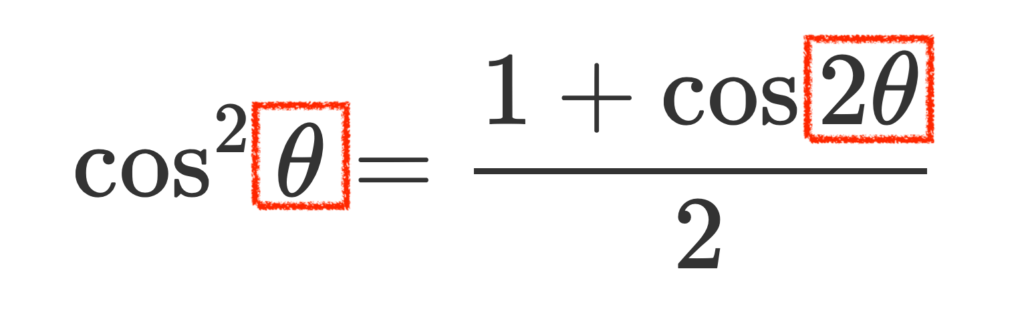


半角を使うメリットとしては、有名角以外の角に対するコサインの値が、すでにわかっている有名角に対するコサインの値に落とし込めるという点です。
次数を下げたいとき
もう1つの使い道は、次数を下げるときです。
主に積分で登場しますが、2乗だと非常に都合が悪い場合がこれから先、多々登場します。
その中で、解決策の1つとして半角の公式を理解しておくといいでしょう。
例題
\(\int cos^2 x \ dx\)の値を求めよ。
半角の公式を見てみると、左辺が2乗の式であるのに対して、右辺は2乗でないところに着目します。
着目ポイント
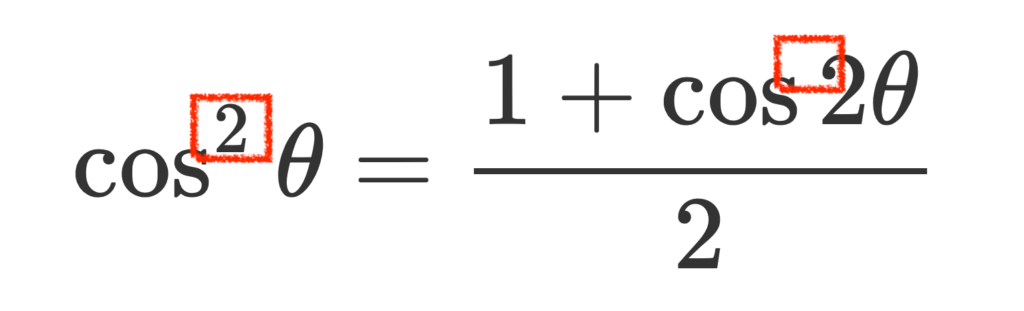
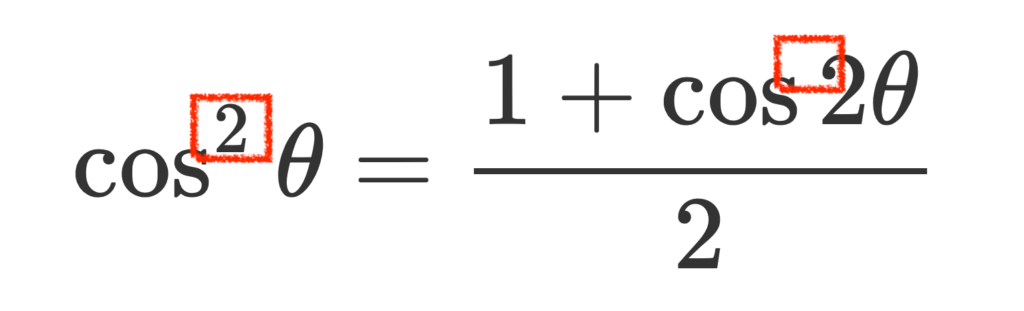


半角の公式|まとめ


まとめ
- $$\sin^2\theta = \frac{1-\cos2\theta}{2}$$
- $$\cos^2\theta = \frac{1+\cos2\theta}{2}$$
- 2倍角の公式から求めることができる。
- 2倍角を使うタイミングは
・微妙な角度を求めるとき
・次数を下げたいとき
この公式を必死に覚えるよりも、加法定理から求められるようになることが力がつきます。
なぜなら、加法定理から
- 2倍角の公式
- 半角の公式
- 積和の公式
- 和積の公式
と多くの公式が求められます。
加法定理の着眼点を変えて式変形するだけなので、全部むやみやたらに覚えるのではなく考え方を学んで欲しいです❤︎


以上、「半角の公式について」でした。
上記例題を参照してください。









