Today's Topic
虚数は\(a+bi(b\neq0)\)と定義され、複素数は\(a+bi(b=0もOK)\)と定義する。




こんなあなたへ
「虚数って何?複素数って何・・・泣」
「実在しない数なんでしょ?考えてどうするの?」
この記事を読むと、この意味がわかる!
- 複素数ってどんな数?虚数との違いは?
- 複素数を考えることで得られるメリットは?

複素数を一気に理解したい方への記事は、こちらにまとめてあります。
Contents
実数と虚数の2つの世界
複素数の単元は、言葉の定義が少しわかりにくいので、ここでしっかり押さえておきましょう。
2次方程式\(x^2=-1\)を考えたとき、
$$x=\pm\sqrt{-1}=\pm i$$
を満たす新たな数、\(i\)を考えます。
この\(i\)を虚数単位と言います。
虚数単位は、要するに二乗すると-1になる数のこと。
これは、これまで人類が考えてきた実数の世界ではあり得ない性質です。
数の集合について復習したい人はこちらを参考にしてください。
続きを見る



【数の集合】自然数とは?整数とは?感覚だけでわかる数の集合


そこで、実数とは異なる新たな数を作っていきます。
人類は\(a,b\)を実数、\(i\)を虚数単位とする数\(a+bi\)を虚数ということにしました。
虚数\(a+bi\)は実部と虚部という2つの部分に分けることができます。
虚数は実数とは異なる数として定義したいので、\(b\neq0\)となります。
実部\(a=0\)のとき、虚数は\(bi\)となり、この状態の数を純虚数といいます。




統一された複素数の世界
ここで数の世界を見つめ直してみると、図のようになっているはずです。
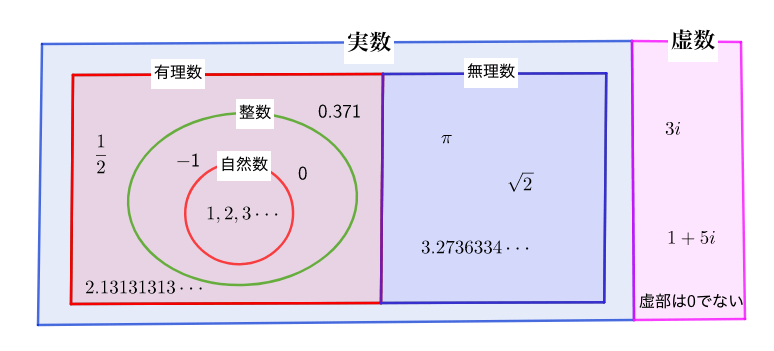



ここで虚数の定義\(a+bi\ (b\neq0)\)を見てみます。
実数とは異なる世界を表現したかったので、\(b\neq0\)としましたが\(b=0\)を許すと実数を表すことができます。
そこで、実数と虚数、どちらも表現できる数の集合として複素数\(a+bi\)を定義します。
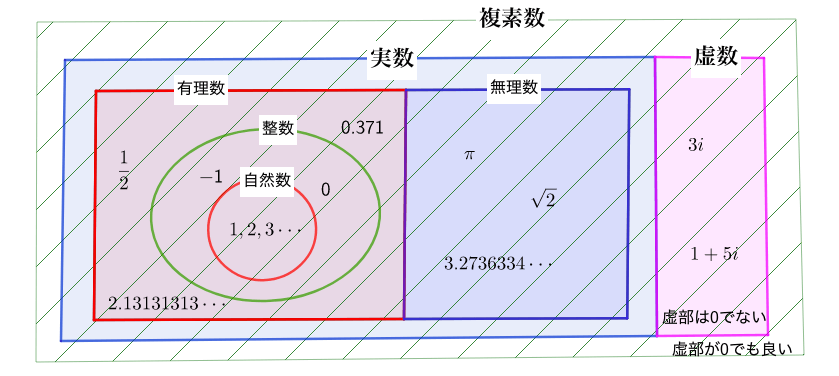



複素数を認めると得られるメリット
虚数を始め、複素数は数学者の間でも"数"として認めるか、かなり議論されました。
長きに渡る議論の末、
複素数を認めちまった方が、いろいろ便利じゃあないか!
ということになり、その存在を認められました笑
では、複素数を認めることで得られるメリットを簡単に紹介していこうと思います。
二次方程式の解が絶対求まる
一番最初に触れておくべきなのは、おそらく虚数が生まれた理由にもなった二次方程式でしょう。
二次方程式\(x^2-x+1=0\)を解の公式で解いてみると、
となります。
\(\sqrt{-3}\)という平方根の定義をガン無視したこの数は、実数では考えることができません。
そのため複素数を認めないのであれば、この二次方程式に解は存在しないということになります。




複素数を数として認めてしまえば、解があるかどうかの議論をせずに済みます。
すなわち、二次方程式の解は絶対解の公式から求められると断言できるようになる、というわけですね。
代数学の基本定理が言える
複素数を認めると、二次方程式\(x^2-x+1=0\)の解は、
or
$$x=\frac{1-\sqrt{3}i}{2} $$
となりました。
では次に、三次方程式\(x^3-1=0\)を解いてみましょう。
と因数分解できるので、\(x^3-1=0\)となるためには
のどちらかを満たす必要があります。
よって答えは、
or
$$x=\frac{-1+\sqrt{3}i}{2}$$
or
$$x=\frac{-1-\sqrt{3}i}{2} $$
となりました。










このように、
ポイント
複素数を認め、重解をそれぞれ1つの解と数えることを約束すると、n次方程式の解はn個ある
ということが言えるようになります。
これを数学では代数学の基本定理と言います。


数Ⅲ複素平面を考えられる
これまで学習した『座標』というものは、横軸に実数\(x\)を、縦軸に実数\(y\)にとってグラフを考えていました。
そのグラフとは別に、横軸に実数\(x\)を、縦軸に純虚数\(yi\)をとって、複素数\(x+yi\)を平面状に描く複素平面というものがあります。
これまでのxy平面
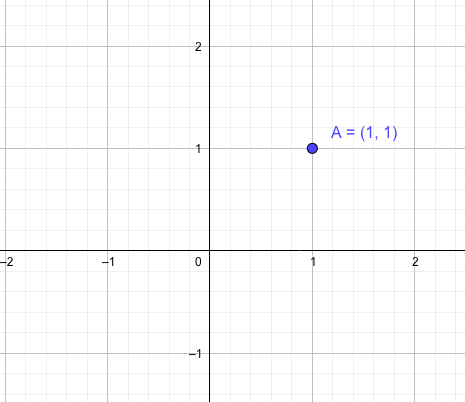

複素平面
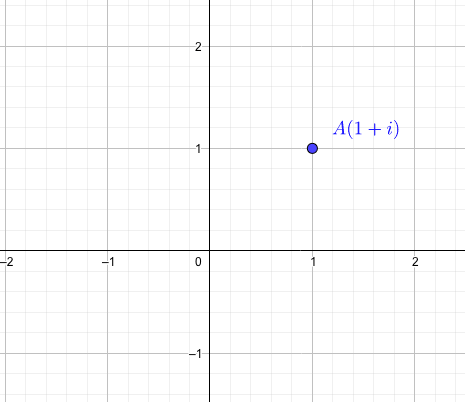

点A:原点から横に1、縦に\(1i\)進んだ点
この複素平面では、\(xy\)平面にはない、面白い性質を見ることができます。
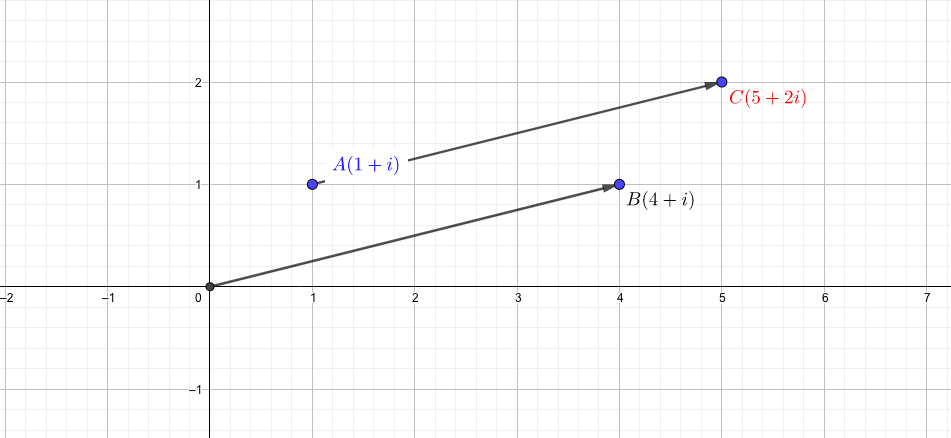
例えば、複素数\(1+i\)に複素数\(4+i\)を加えると、\(5+2i\)になりますが、これを複素平面上で考えると、平行移動を表します。



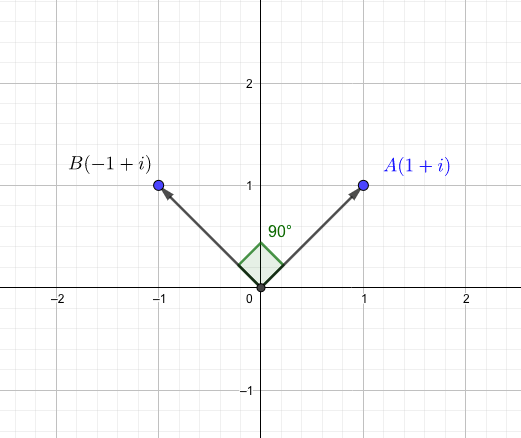
また、複素数\(1+i\)を\(i\) 倍すると、
となりますが、これを複素平面上で考えると、90度回転していることがわかります。

このように
ポイント
- 2つの複素数の和→平行移動
- 2つの複素数の積→回転移動
というかなり面白い性質が見られました。
特に後者の回転移動は、\(xy\)平面で考えると行列という考え方を使った、ちょっとめんどくさい計算が必要になります。
よって複素平面で考えられることは十分有意義であり、電子工学等では欠かせない単元になっています。
複素平面について知りたい人はこちらを参考にしてください。
続きを見る



複素平面の特徴と軌跡→xy平面に戻すor直線や円、二等分線の形になおす
まとめ|複素数は世界を広げる


まとめ
- \(\sqrt{-1}= i\)とする。
- \(i\)を虚数単位という。
- 2乗すると負になるという実数にはない性質を持つ数の虚数を\(a+bi(b\neq0)\)と定義する。
- \(a+bi\)について\(b=0\)を許すと、実数範囲まで表せる。この数を複素数という。
- \(a\)を実部、\(b\)を虚部といい、\(a=0,b\neq0\)の複素数を純虚数という。
- 複素数を認めると、いろんなメリットがある。
複素平面について、実際に触れるのは理系の方だけだと思いますが、\(xy\)平面にはない性質があって、結構面白いでしょう?
あなたがこれまでに抱いてきた
「複素数ってなによ?考えていいことあるか?」
という感覚は、先人の数学者たちも思っていたことです。


数として認めることで、多くのメリットを得ることができる。
数学はそうやって便利なものをどんどん吸収して、ここまでやってきたんですね。
「複素数をOKにすると、いろんなものがOKになって便利になる!」
と思えれば、十分だと思いますよ。
以上、「複素数の言葉の定義と考える意味について」でした。
- 実数とは異なる数として定義されたのが虚数\(a+bi\ (b\neq 0)\)。
実数まで含めて考えた数が複素数\(a+bi\)。 - 二次方程式の解を絶対に求めることができたり、代数学の基本定理が言えたり。









