複素平面の特徴と軌跡→xy平面に戻すor直線や円、二等分線の形になおす

Today's Topic

複素平面上では、

中心が$\alpha$、半径rの円：$|z-\alpha| = r$

$\alpha$と$\beta$の垂直二等分線：$|z-\alpha|=|z-\beta|$

楓

よし、今回は複素平面の基本的なグラフについてみていくよ！

複素数って不思議なルールが多いし、なんだか不安だなあぁ。

小春

楓

複素平面は、ベクトル方程式を比較すると、実は全く同じことを考えていることに気がつくと思うよ。

ベクトル方程式と一緒なの？！

小春

楓

そう、あとは計算のしやすさとかの問題。今回はベクトル方程式との比較や、裏ワザも一緒に紹介していくね！

こんなあなたへ

「複素平面ってxy平面となんでこんなに違うの？」

「円や二等分線がどうしてあんな式になるの？」

この記事を読むと、この意味がわかる！

複素平面上で、$(2-i)z+(2+i)\overline{z}=10$を満たす複素数zが描く軌跡を求めよ。
複素平面上で、$|z-3i|=2|z|$を満たす複素数zが描く軌跡を求めよ。

答えは一番最後にあるよ！

楓

複素数を一気に理解したい方への記事は、こちらにまとめてあります。

まとめ記事

: 【複素数公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ（数Ⅱ・数Ⅲ対応）

続きを見る

Contents

1 複素平面の概要
2 複素平面を考えたときの和と積
3 複素平面上での対称移動
4 複素平面上でのグラフ
5 【裏ワザあり】複素平面上の軌跡の求め方
- 5.1 知っている軌跡の形にごり押し
- 5.2 【裏ワザ】$xy$平面に置き換える
6 まとめ

複素平面の概要

これまで学習した『座標』というものは、横軸に実数$x$を、縦軸に実数$y$にとってグラフを考えていました。

そのグラフとは別に、横軸に実数$x$を、縦軸に純虚数$yi$をとって、複素数$x+yi$を平面状に描く複素平面というものがあります。

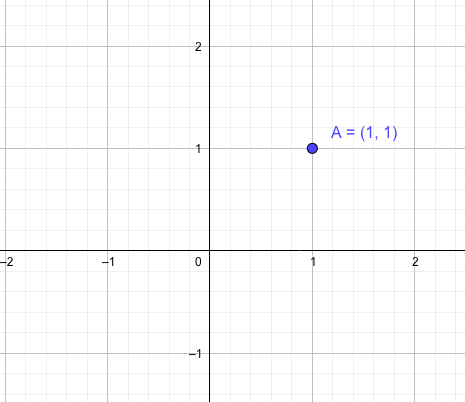
これまでのxy平面

点A：原点から横に1、縦に1進んだ点

複素平面

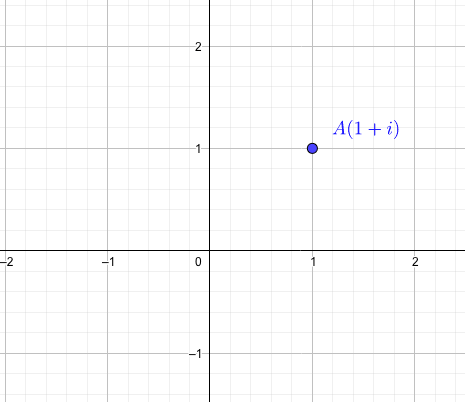
点A:原点から横に1、縦に$1i$進んだ点

この２つの大きな違いは、ある1点を表すときに座標を使うのか、１つの数を使うのかです。

楓

上で挙げた図は、同じ点を表しているよ。

$(1,1)$と実数の組で表すか、$1+i$と１つの数で表すかの違いのことだね。

小春

$xy$平面では点Aの位置を$A(1,1)$と表し、複素平面では点Aの位置を$A(1+i)$と表します。

これによって、複素平面はベクトルを考えやすいという利点が生まれます。

小春

$xy$平面だとベクトル$$\overrightarrow{OA}=\begin{pmatrix}1 \\ 1 \\ \end{pmatrix}$$と表すね。

対して、複素平面だと$1+i$そのものが$\overrightarrow{OA}$を表しているんだ！

楓

複素平面を考えたときの和と積

複素数の和と積は、$xy$平面では見られないような動きをします。

例えば複素数$1+i$に複素数$4+i$を加えると、$5+2i$になりますが、これを複素平面上で考えると、平行移動を表しています。

楓

２つの複素数の和を表す点Cは、点$A(1+i)$からOBベクトルだけ移動させた点になっているね。

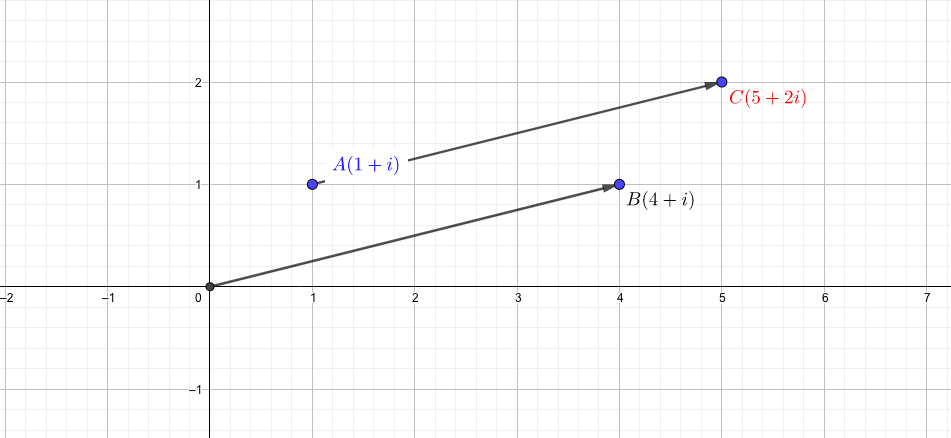
また、複素数$1+i$を$i$ 倍すると、

$$i(1+i)=i-1=-1+i$$

となりますが、これを複素平面上で考えると、90度回転していることがわかります。

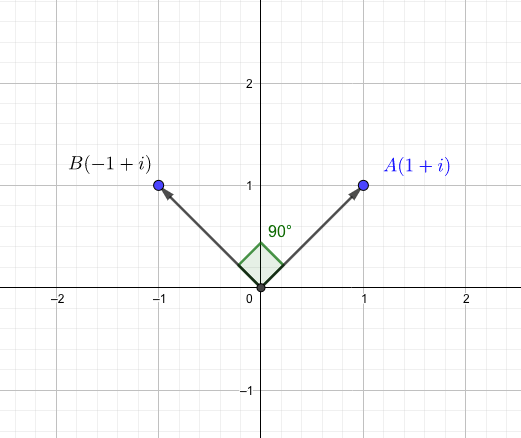
このように

ポイント

２つの複素数の和→平行移動
２つの複素数の積→回転移動

というかなり面白い性質が見られました。

特に後者の回転移動は、$xy$平面で行う場合、行列を使ったちょっとめんどくさい計算が必要になります。

これらの理由については、下記記事を参照してください。

複素数の四則の本質について復習したい人はこちらを参考にしてください。

: 【複素数の計算】徹底攻略！複素数の四則→図形の伸縮と回転

続きを見る

複素平面上での対称移動

複素数$\alpha=1+i$と、共役な複素数$\overline{\alpha}=1-i$を複素平面上にプロットすると、実軸対象になっていることがわかります。

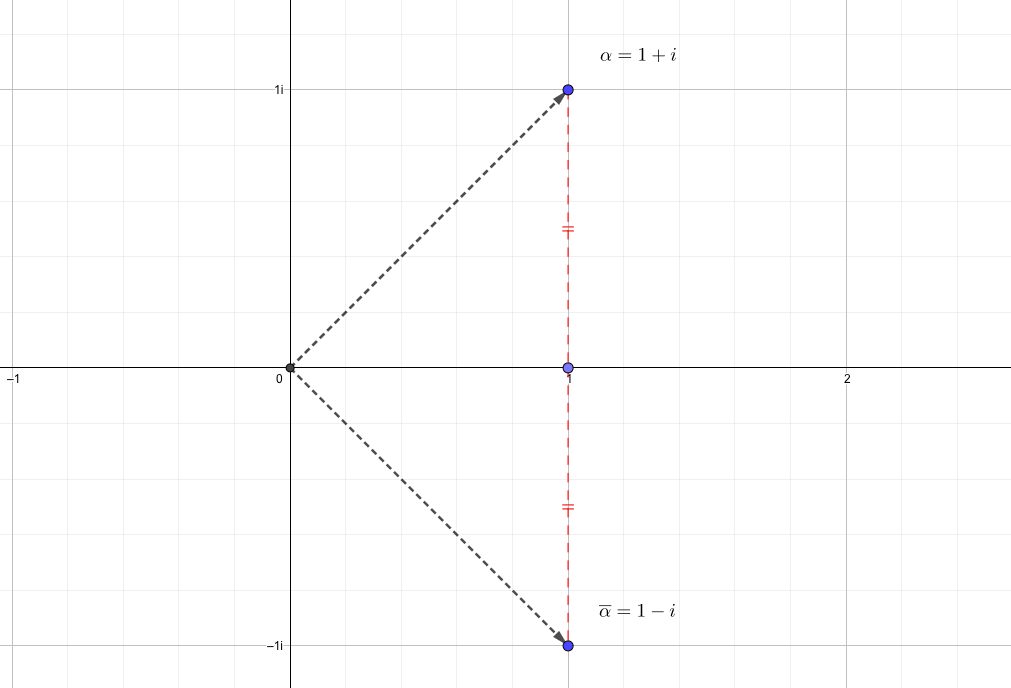
共役な複素数の性質について復習したい人はこちらを参考にしてください。

: 共役な複素数の重要性質４つ→特殊計算・分割可能・方程式の解・複素平面

続きを見る

では$\alpha$に対して、実部の符号が入れ替わった$\beta=-1+i$と、その共役な複素数$\overline{\beta}=-1-i$を複素平面上に一気にプロットしてみます。

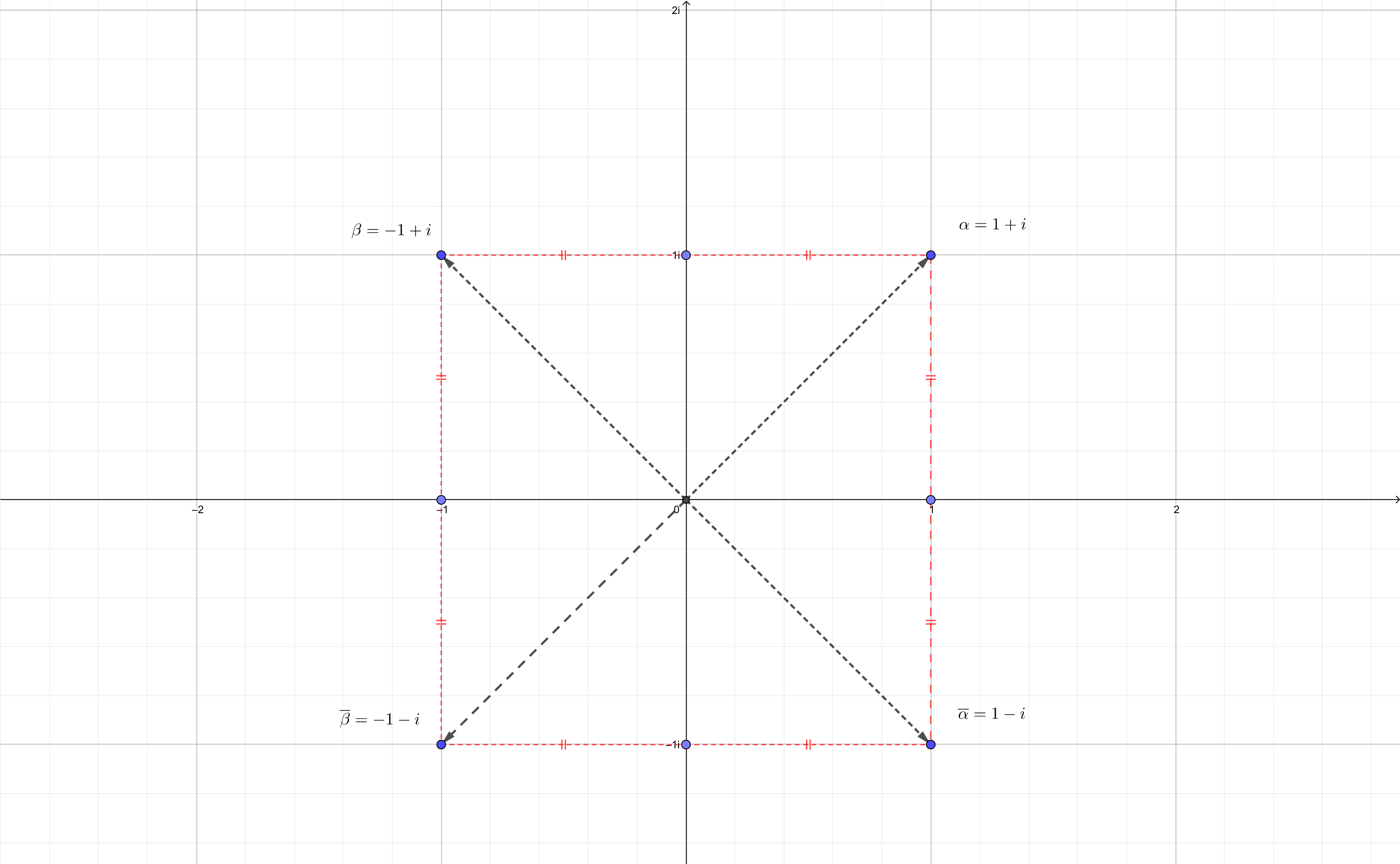
図からも分かる通り、

ポイント

共役な複素数：実軸対象
実部の符号が逆：虚軸対象

となります。

複素平面上でのグラフ

ここでは、複素平面では今まで慣れ親しんできた

2点間の距離
垂直二等分線
円

がどのような式で描けるのかを解説していきます。

2点間の距離

この2点間の距離の考え方が、$xy$平面と複素平面の架け橋になるので、絶対に理解してください！！

$xy$平面上では、2点A,Bの距離は位置ベクトルを用いて、次のように表せます。

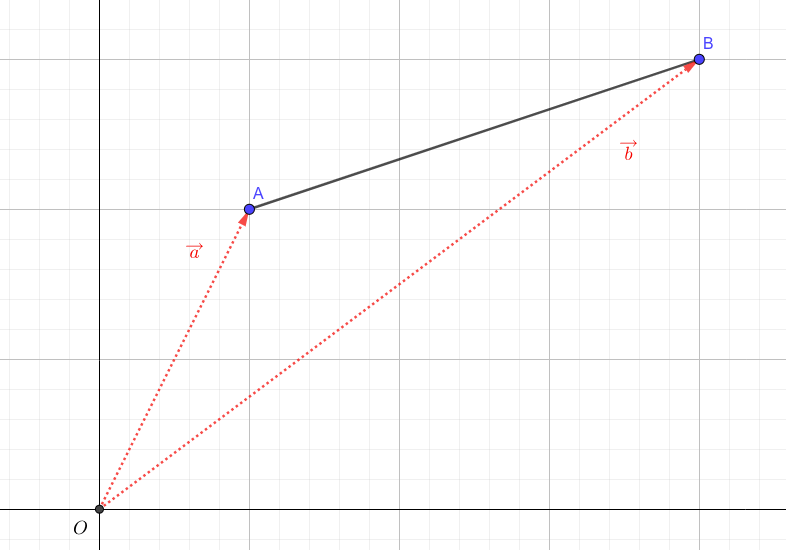
$$AB=|\overrightarrow{b}-\overrightarrow{a}|$$

具体的な距離の長さを測るためには、三平方の定理を活用します。

$\overrightarrow{a}=\begin{pmatrix}a_x \\ a_y \\ \end{pmatrix},\overrightarrow{b}=\begin{pmatrix}b_x \\ b_y \\ \end{pmatrix}$としたとき、三平方の定理を用いると次のように求められます。

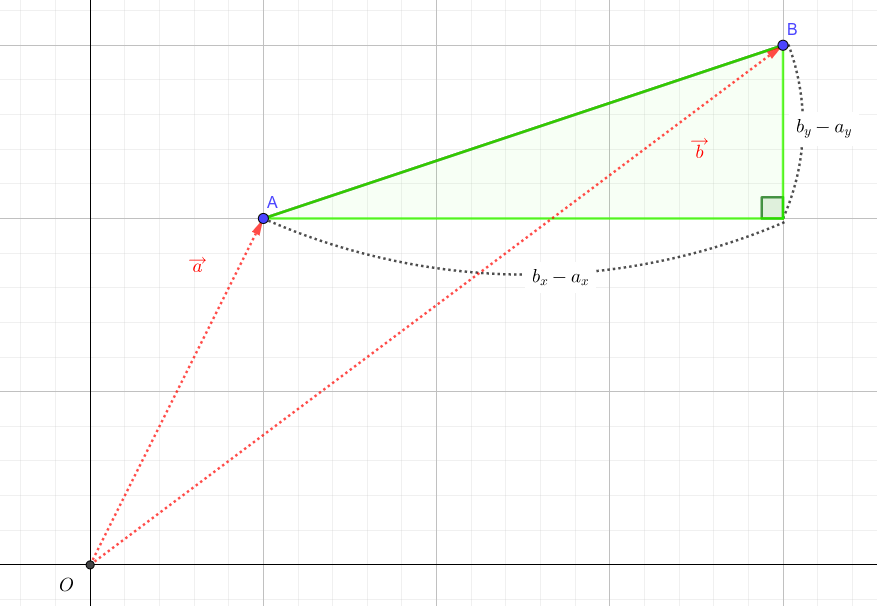
$$AB=\sqrt{\left(b_y-a_y\right)+\left(b_y-a_y\right)^2}$$

複素平面では、このベクトルを複素数に丸ごと置きかえることができます。

2点$A(\alpha),B(\beta)$の距離は（位置ベクトルを意識して）、次のように表せます。

ポイント

$$AB=|\beta-\alpha|$$

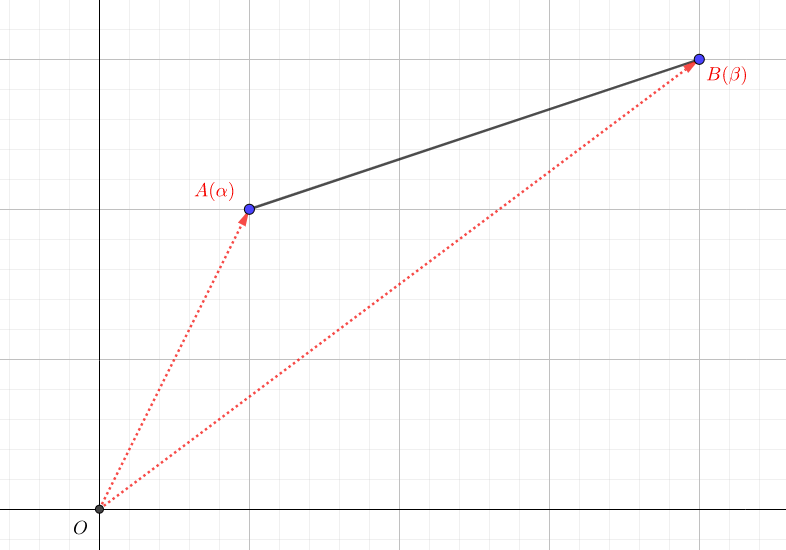
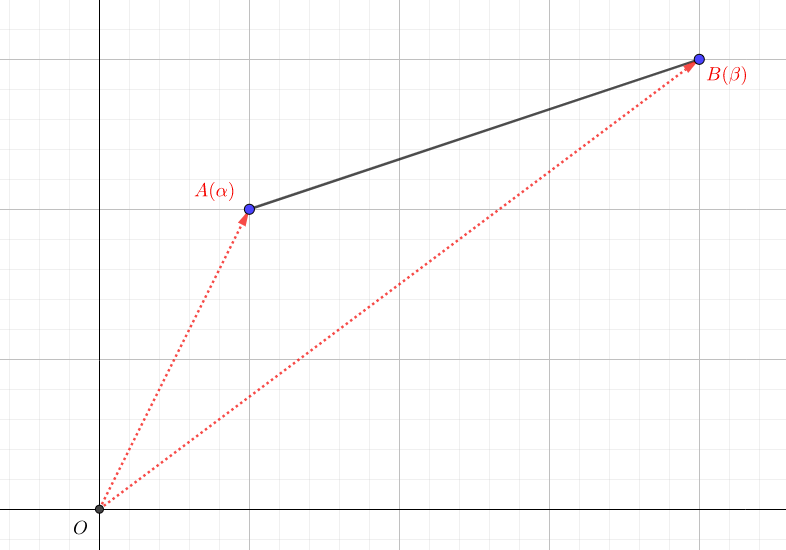
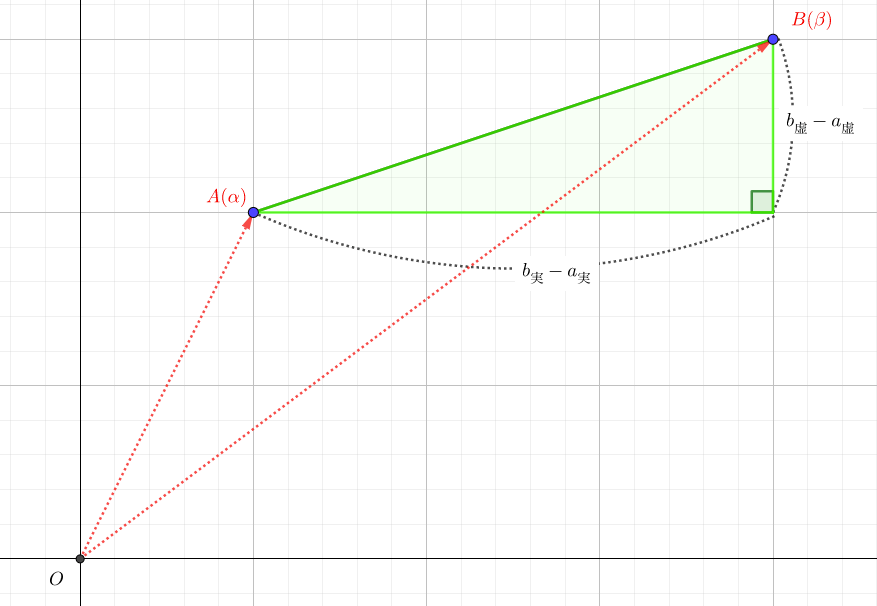
複素平面の場合も、具体的な距離の長さを測るためには、三平方の定理を活用します。

$\alpha=a_実+a_虚i,\beta=b_実+b_虚i$としたとき、三平方の定理を用いると次のように求められます。

$$AB=\sqrt{\left(b_実-a_実\right)+\left(b_虚-a_虚\right)^2}$$

前述の通り、複素数はベクトルがかなり意識しやすいです。

そのため今回のように、$xy$平面でベクトルとして扱っていたものをそのまま、複素平面に置き換えるとわかりやすくなります。

二等分線

複素平面上で、垂直二等分線は次のように表せます。

ポイント

$$|z-\alpha|=|z-\beta|$$

を満たす複素数zの軌跡は、2点$A(\alpha),B(\beta)$の垂直二等分線となる。

小春

え、なんで？？？

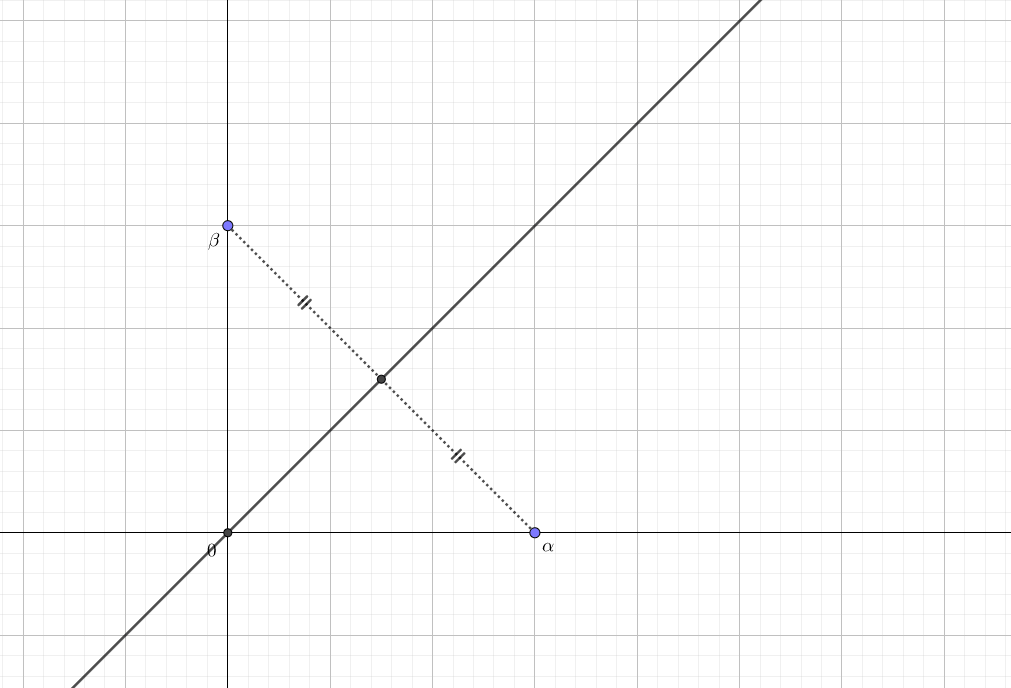
と思う方も多いと思います。

しかし、式の言っている意味は

『$z$から$\alpha$までの距離と、$z$から$\beta$までの距離が等しい』ような$z$の集まり

ととても単純なものです。

$xy$平面でもベクトルを用いて、

$$|\overrightarrow{p}-\overrightarrow{a}|=|\overrightarrow{p}-\overrightarrow{b}|$$

と表せる点$P(\overrightarrow{p})$は、2点$A(\overrightarrow{a}),B(\overrightarrow{b})$の垂直二等分線を表しますね。

楓

$\overrightarrow{p},\overrightarrow{a},\overrightarrow{b}$はそれぞれ位置ベクトルを表すよ。

ベクトルと複素平面は、基本的に考え方が同じものなんだね。

小春

円

複素平面上で、円は次のように表せます。

ポイント

$$|z-\alpha|=r$$

を満たす複素数$z$の軌跡は、中心$A(\alpha)$、半径$r$の円を描く。

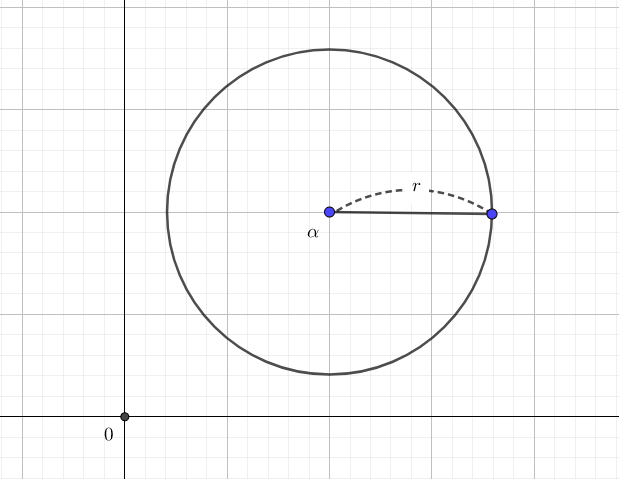
複素平面が理解しにくい時は、一度ベクトル方程式まで戻ってみましょう。

$xy$平面でもベクトルを用いて、

$$|\overrightarrow{p}-\overrightarrow{a}|=r$$

と表せる点$P(\overrightarrow{p})$は、点$A(\overrightarrow{a})$中心、半径$r$の円を描きますね。

楓

$\overrightarrow{p},\overrightarrow{a}$はそれぞれ位置ベクトルを表すよ。

これをみた後だと、円を表す複素方程式の意味もだいぶ理解しやすいのではないでしょうか。

【裏ワザあり】複素平面上の軌跡の求め方

ここでは、

『与えられた式が複素平面上でどのようなグラフ（軌跡）を描くか』

と問われた際の解決策をご紹介します。

覚える手法は２つだけ！

知っている軌跡の形にごり押し

では次のような問題を見てみましょう。

例題

$|z|^2+iz-i\overline{z}=1$を満たす複素数$z$が描く軌跡を求めよ。

小春

このままだと、なんのグラフかわからないよ・・・

これを$|z|^2=z\overline{z},\overline{i}=-i$に注意して、次のように変形させてみます。

\begin{align} |z|^2+iz-i\overline{z} &= z\overline{z}-\overline{i}z-i\overline{z}\\\ &= (z-i)(\overline{z}-\overline{i})-i\overline{i}\\\ \end{align}

ここで共役な複素数の性質

分割可能
実数化

を使うと

$(\overline{z}-\overline{i})=\overline{(z-i)}$
$i\overline{i}=1$

が導けます。

楓

あ、ちょっと共役の性質やばいなぁと思ったら復習しとき

共役な複素数の性質について復習したい人はこちらを参考にしてください。

: 共役な複素数の重要性質４つ→特殊計算・分割可能・方程式の解・複素平面

続きを見る

よって、

\begin{align} (z-i)(\overline{z}-\overline{i})-i\overline{i} &= (z-i)(\overline{z}-\overline{i})=\overline{(z-i)}-1\\\ &= |z-i|^2-1\\\ \end{align}

（※見切れている場合はスクロール）

と変形できます。

楓

最後は$z\overline{z}=|z|^2$を使ったよ。

つまり

$$|z-i|^2-1=1\iff|z-i|=\sqrt{2}$$

が得られ、これは複素平面上では半径$\sqrt{2}$、中心A$(i)$の円を表します。

このように、自分の知っている形に無理やり変形するという手法があります。

この手法は慣れるまでなんども行う必要があり、まるで武者修行のようですが、慣れると大体式を見ただけで何をすればいいかがわかるようになります。

時間をかけて習得することをオススメします。

【裏ワザ】$xy$平面に置き換える

ここでご紹介する方法は裏ワザ的。

複素平面ちゃんから、慣れ親しんだ$xy$平面ちゃんに戻して考えます。

例題

$|z-3i|=2|z|$を満たす$z$の軌跡を求めよ。

楓

本来は$z\overline{z}=|z|^2$の性質を使ってぐちゃぐちゃやって欲しいんだけどね。

裏ワザのやり方は簡単、$z=x+yi$($x,y$は実数)に置き換えてしまうことです。

すると与式は$|x+(y-3)i|=2|x+yi|$と書き換えられます。

ちなみに

複素数で絶対値｜｜が出たら、まぁどんな場合も大体両辺2乗します。

楓

これ冗談のようで、マジよ。$z\overline{z}=|z|^2$に持って行いきたいわけよ。

というわけで、両辺2乗して、$z\overline{z}=|z|^2$に注意して式変形していきます。

$$\left(|x+(y-3)i|\right)^2=\left(2|x+yi|\right)^2 \iff x^2+(y-3)^2=4(x^2+y^2)$$

（※見切れている場合はスクロール）

楓

共役の性質で$z\overline{z}$は実数化して、実部と虚部の2乗の和が残るんだったね。

移項して

\begin{align} x^2+(y-3)^2-4(x^2+y^2) &= 3x^2+3y^2+6y-9\\\ &= 3x^2+3(y^2+2y)-9\\\ \end{align}

（※見切れている場合はスクロール）

となるので、

$$3x^2+3(y^2+2y)=9$$

が得られます。

両辺$\frac{1}{3}$倍して

$$x^2+(y^2+2y)=3$$

式変形して、

$$x^2+(y+1)^2-1=3$$

よって、

$x^2+(y+1)^2=4$

が得られました。

これは$xy$平面では、中心$(0,-1)$、半径2の円を描きます。

最後に得られた結果を複素平面の世界に戻します。

つまり

$z$の軌跡は中心$0-i$、半径2の円を描く

ということになります。

複素数の形でゴリゴリやっていると、これは「アポロニウスの円だな」と気付けるようになるのですが、

「どうしても複素数嫌なんじゃぁ」

という方は、この手法がオススメです。

アポロニウスの円について復習したい人はこちらを参考にしてください。

まとめ

楓

お疲れ様、まとめです。

まとめ

複素平面は、xy平面のベクトルと対応する。
距離：$AB=|\beta-\alpha|$
垂直二等分線：$|z-\alpha|=|z-\beta|$
円：$|z-\alpha|=r$
複素平面乗の軌跡を考えるためには、
　・知っている形にごり押しする
　・$xy$平面に戻して考える
のようにすれば良い。
$z\overline{z}=|z|^2$は大事

最後に紹介した$xy$平面に戻すというやり方はあくまで、どうしてもわからない場合に使って欲しい手段です。

複素平面の世界だけで考えることでその利便性や特徴がわかったり、ベクトルの理解も深まります。

また、今回の記事で共役複素数の性質$z\overline{z}=|z|^2$がむちゃくちゃ出てきました。

それくらい共役複素数の性質は重要です。

はい、復習。

共役な複素数の性質について復習したい人はこちらを参考にしてください。

: 共役な複素数の重要性質４つ→特殊計算・分割可能・方程式の解・複素平面

続きを見る

以上、「複素平面について」でした。

最初の答え
Q.複素平面上で、$(2-i)z+(2+i)\overline{z}=10$を満たす複素数zが描く軌跡を求めよ。

$z=x+yi$($x,y$は実数)とおくと与式は

$$(2-i)(x+yi)+(2+i)(x-yi)=10$$

（※見切れている場合はスクロール）

となる。展開してまとめると、

$$(2x+y+2x+y)+(-x+2y+x-2y)i=10$$

（※見切れている場合はスクロール）

$$4x+2y=10$$

よって、$y=-2x+5$となるのでzの軌跡は傾き$-2$、切片$5i$の直線を描く。

Q.複素平面上で、$|z-3i|=2|z|$を満たす複素数zが描く軌跡を求めよ。

例題参照

複素平面の特徴と軌跡→xy平面に戻すor直線や円、二等分線の形になおす

【複素数公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ（数Ⅱ・数Ⅲ対応）

複素平面の概要

複素平面を考えたときの和と積

【複素数の計算】徹底攻略！複素数の四則→図形の伸縮と回転

複素平面上での対称移動

共役な複素数の重要性質４つ→特殊計算・分割可能・方程式の解・複素平面

複素平面上でのグラフ

2点間の距離

二等分線

円

【裏ワザあり】複素平面上の軌跡の求め方

知っている軌跡の形にごり押し

共役な複素数の重要性質４つ→特殊計算・分割可能・方程式の解・複素平面

【裏ワザ】\(xy\)平面に置き換える

まとめ

共役な複素数の重要性質４つ→特殊計算・分割可能・方程式の解・複素平面

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則