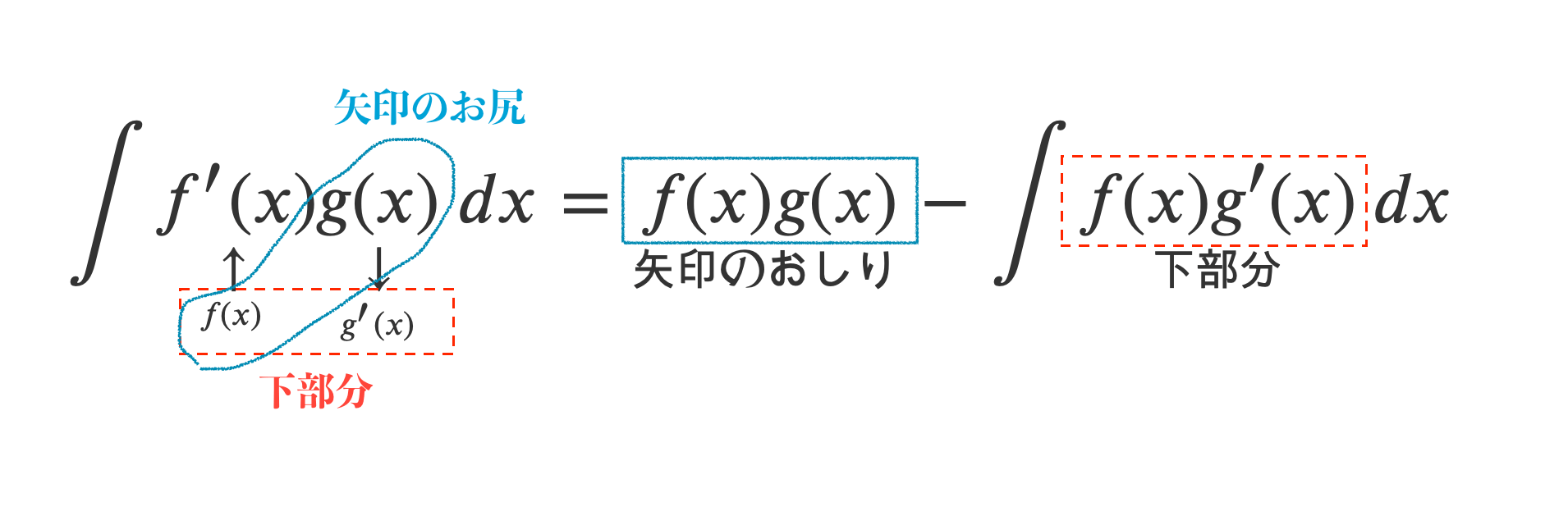Today's Topic
$$\small{\int f(x)g’(x)dx = f(x)g(x)\ - \int f’(x)g(x)dx} $$
(※見切れている場合はスクロール)

小春
楓くん、部分積分って公式が成り立つ理由はなんとなくわかるけど、使い方が全くわからない〜泣
部分積分法には、あるコツがあるんだ。公式の成り立ちよりも、使い方のコツが大事かな。

楓

小春
僕はパッと積分できないなと思ったら、最初にまず部分積分を試すくらいだよ笑

楓

小春
え〜、ムッチャ使えるじゃん!それなら、部分積分法のコツを教えて欲しいな!
この記事を読むと、この問題が解ける!
- $$\int_0^\pi x\sin xdx$$
- $$\int e^{x}\cos xdx$$

楓
【これだけでOK】部分積分のコツ→下書きをする
部分積分をなかなか実践場面で使えない、あるいは使っても間違ってしまう理由としては、公式をそのまま覚えていることに理由があります。
例えば、
$$\int x\log x\ dx=\frac{1}{2}x^2\log x - \int \frac{1}{2}x\ dx$$
なんかは代表的な部分積分の問題ですが、公式と見比べて同じ形に見える人はそう多くないと思います。

小春
確かに公式そのものはわかるけど、いざ問題見てその形と同じに見えるかって言われるとねぇ。
そこで部分積分を使うコツとして、下書きをすることをオススメします。

小春
下書きとは、
$$\int\underset{\underset{\frac{1}{2}x^2}{\uparrow}}{x}\underset{\underset{\frac{1}{x}}{\downarrow}}{\log x} \ dx $$
のように、
↑↓を使って、一方は積分した値、もう一方は微分した値を書いておく
というものです。

楓
ポイント
部分積分を上手にするためには
$$\int\underset{\underset{f(x)}{\uparrow}}{f'(x)}\underset{\underset{g'(x)}{\downarrow}}{g(x)}\ dx$$
の下書きを施すとよい。
このようにすると、
\begin{align} \int\underset{\underset{\overset{\frac{1}{2}x^2}{\color{red}{f}}}{\uparrow}}{\overset{\color{red}{f'}}{x}}\underset{\underset{\overset{\frac{1}{x}}{\color{blue}{g'}}}{\downarrow}}{\overset{\color{blue}{g}}{\log x}} \ dx &= \underset{\color{red}{f}}{\frac{1}{2}x^2}\underset{\color{blue}{g}}{\log x} - \int \underset{\color{red}{f}}{\frac{1}{2}x^2}\cdot\underset{\color{blue}{g'}}{\frac{1}{x}}\ dx\\\ &= \frac{1}{2}x^2\log x - \frac{1}{4}x^2 +C\\\ \end{align}
(※見切れている場合はスクロール)
となります。
矢印の向きに着目すると部分積分は、
ポイント
$$\small{\int\underset{\underset{f(x)}{\uparrow}}{f'(x)}\underset{\underset{g'(x)}{\downarrow}}{g(x)}\ dx = \underset{矢印のおしり}{f(x)g(x)} - \int \underset{下部分}{f(x)g'(x)}\ dx}$$
(※見切れている場合はスクロール)
と覚えることができます。
部分積分は2回試せ
と思って試してみて、うまくいかなくても入れ替えて試してみるとうまくいく場合があります。
具体例を見てみましょう。
これを
$$\int \underset{\frac{x^2}{2}}{\underset{\uparrow}{x}} \underset{\underset{\cos x}{\downarrow}}{\sin x} dx$$
のように下書きしてみました。
ではこれで部分積分してみると・・・
\begin{align} \int \underset{\frac{x^2}{2}}{\underset{\uparrow}{x}} \underset{\underset{\cos x}{\downarrow}}{\sin x} dx &= \underset{矢印のおしり}{\frac{x^2}{2}\sin x}-\int \underset{下部分}{\frac{x^2}{2} \cos x}dx\\\ \end{align}
(※見切れている場合はスクロール)

小春
ゲッ、$$\int \underset{下部分}{\frac{x^2}{2} \cos x}dx$$なんてわからないよ泣
もう一回部分積分する方法もあるけど、やりたくないよね。

楓
ここでうまくいかない場合でも部分積分ではないと決めつけるのではなく、↑↓の順番を↓↑に変えてやってみると
$$\int \underset{1}{\underset{\downarrow}{x}} \underset{\underset{-\cos x}{\uparrow}}{\sin x} dx$$
となり、
\begin{align} \int \underset{1}{\underset{\downarrow}{x}} \underset{\underset{-\cos x}{\uparrow}}{\sin x} dx &= \underset{矢印のおしり}{-x\cos x}-\int \underset{下部分}{-\cos x}dx\\\ &= -x\cos x+\sin x +C\\\ \end{align}
のようにうまく求めることができました。

楓
矢印の順序を入れ替えても、$$矢印のおしり- \int 下部分 dx$$は変わらないよ。
後述しますが、「これ部分積分でイケそう」と思うときは大体部分積分でイケます笑
あとは↑↓でするか、↓↑でするかのどちらか。
一発でうまくいかなくても、二発目までは試してみてください。

小春
定積分の場合の部分積分
これまでの例では不定積分で行いましたが、定積分もそれほど変わりません。
例題
$$\int_0^\pi x\sin x dx$$
↓↑の順番で部分積分を行うと
\begin{align} \int_0^\pi \underset{1}{\underset{\downarrow}{x}} \underset{\underset{-\cos x}{\uparrow}}{\sin x} dx &= \left[\underset{矢印のおしり}{-x\cos x}\right]_0^\pi-\int_0^\pi \underset{下部分}{-\cos x}dx\\\ &= \pi+\left[\sin x\right]_0^\pi \\\ &= \pi \\\ \end{align}
(※見切れている場合はスクロール)
となります。

楓
要は\(\int\)が外れたところから、ちゃっちゃと代入していけばいいんだね。
【ピンとくるようになる】部分積分が使える場面
ここでは部分積分が使える2つの例題をご紹介します。
この2つの例題を知っているだけで、「こいつ部分積分でイケそうだな」という感がしっかり身につきますよ!
【場面①】2つの関数の積|\(\log \)や\(\cos \)があると可能性大
1つ目の例題は、2つの関数の積で表されたものの積分です。
中でも\(\cos\)や\(\log\)、\(e^x\)が含まれているときは、とりあえず部分積分から試します。
\(e^x\)は微分しても積分しても同じなので、\(x\)を微分して1にすることで求めることができそうです。
\begin{align} \int \underset{\underset{1}{\downarrow}}{x}\underset{\underset{e^x}{\uparrow}}{e^x}dx &= xe^x-\int e^x dx\\\ &= (x-1)e^x+C\\\ \end{align}

楓
【例外】\(\log x\)の積分
ここでついでに1つだけ、有名な例外を紹介しておきましょう。
\(\log x\)は2つの異なる関数の積では表されていません。
しかし、この積分だけどーーーーしてもできなかったので、強引に部分積分に帰着させます。
\begin{align} \int \underset{\underset{x}{\uparrow}}{1}\cdot\underset{\underset{\frac{1}{x}}{\downarrow}}{\log x}dx &= x\log x-\int 1 dx\\\ &= x\log x -x+C\\\ \end{align}

楓
1を「\(x\)が微分されたもの」とみなすことで部分積分を適用するんだ。

小春
【場面②】指数関数×三角関数
指数関数と三角関数の積で表されるものの積分は、部分積分を用いたちょっと特殊な解法をします。
↑↓の順に2回部分積分を行うと、
\begin{align} \int \underset{\underset{e^x}{\uparrow}}{e^x} \underset{\underset{-\sin x}{\downarrow}}{\cos x} dx &= \int e^x\cos x + \int \underset{\underset{e^x}{\uparrow}}{e^x} \underset{\underset{\cos x}{\downarrow}}{\sin x} dx\\\ &= e^x\cos x + e^x\sin x -\int e^x \cos x dx\\\ \end{align}
(※見切れている場合はスクロール)
となります。

小春
えー、これ何回部分積分しても終わらないんじゃない?
ところが、この式をよくみてみるとループしていることに気がつくよ。

楓

小春
\begin{align} \color{red}{\int \underset{\underset{e^x}{\uparrow}}{e^x} \underset{\underset{-\sin x}{\downarrow}}{\cos x} dx} &= \int e^x\cos x + \int \underset{\underset{e^x}{\uparrow}}{e^x} \underset{\underset{\cos x}{\downarrow}}{\sin x} dx\\\ &= e^x\cos x + e^x\sin x -\color{red}{\int e^x \cos x dx}\\\ \end{align}
(※見切れている場合はスクロール)

小春
ほ、ほんとだ!求める積分の値が式変形でまた出てきた!

楓
\(\color{red}{\int e^x \cos x dx}\)を移項すると、
$$2\color{red}{\int e^x \cos x dx} =e^x\cos x + e^x\sin x$$
よって、
$$\color{red}{\int e^x \cos x dx} =\frac{1}{2}\left(\cos x + \sin x\right)e^x+C$$
(※見切れている場合はスクロール)
部分積分法の証明
証明自体は、積の微分法を用いることで簡単に求められます。
ポイント
$$\left\{f(x)g(x)\right\}'= f'(x)g(x)+f(x)g'(x)$$
積の微分法について復習したい人はこちらを参考にしてください。
移項すると、
$$f(x)g'(x)= \left\{f(x)g(x)\right\}'-f'(x)g(x)$$
となり、両辺\(x\)で積分すると、
$$\int f(x)g’(x)dx = f(x)g(x)\ - \int f’(x)g(x)dx $$
(※見切れている場合はスクロール)
が得られます。
これをさらに移項して、
$$\int f'(x)g(x)dx = f(x)g(x)\ - \int f(x)g'(x)dx $$
(※見切れている場合はスクロール)
が得られることから、↑↓の順でやっても↑↓の順でやっても成立することがわかります。
まとめ

楓
微分と違い、積分はうまく求まるかどうかが非常に怪しいもの。
部分積分以外にもまだまだ多くの積分手法があります。
それらと比較しても、部分積分は下書きさえすれば非常に使いやすいものだと思います。
ぜひこの記事を読み直して、マスターしてください。
以上、「部分積分について」でした。