【区分求積法】なぜ定積分は面積を表すの？文理どっちでも理解できるよう優しく解説

楓

今回は定積分の本質に迫っていこうと思うよ。

不定積分は計算法則として、定積分は面積としての意味合いが強いって言ってたね。

小春

楓

その通り、今回は『なぜ定積分が面積を表すのか』について熱く語ります！

ほどほどに、、、ね。

小春

そもそも面積とは何か

楓

小学校算数の復習から入るよ笑

面積の導入として初めて触れるのは、タテ\(\times\)ヨコの長方形の面積です。

この公式は、長方形の中に面積1の単位正方形がいくつか、を数えることで面積を求めるという発想です。

楓

例えば図の場合だと、\(3\times5\)をすると、単位正方形の個数をささっと数えられるね。

しかし長方形は線分だけで囲まれた図。

曲線の場合だと、同じように単位正方形がいくつ分かを数えることが難しくなります。

具体的な例を見てみましょう。

図の斜線部のような、区間\(0≦x≦5\)において関数\(f(x)\)と\(x\)軸とで囲まれた面積を考えます。

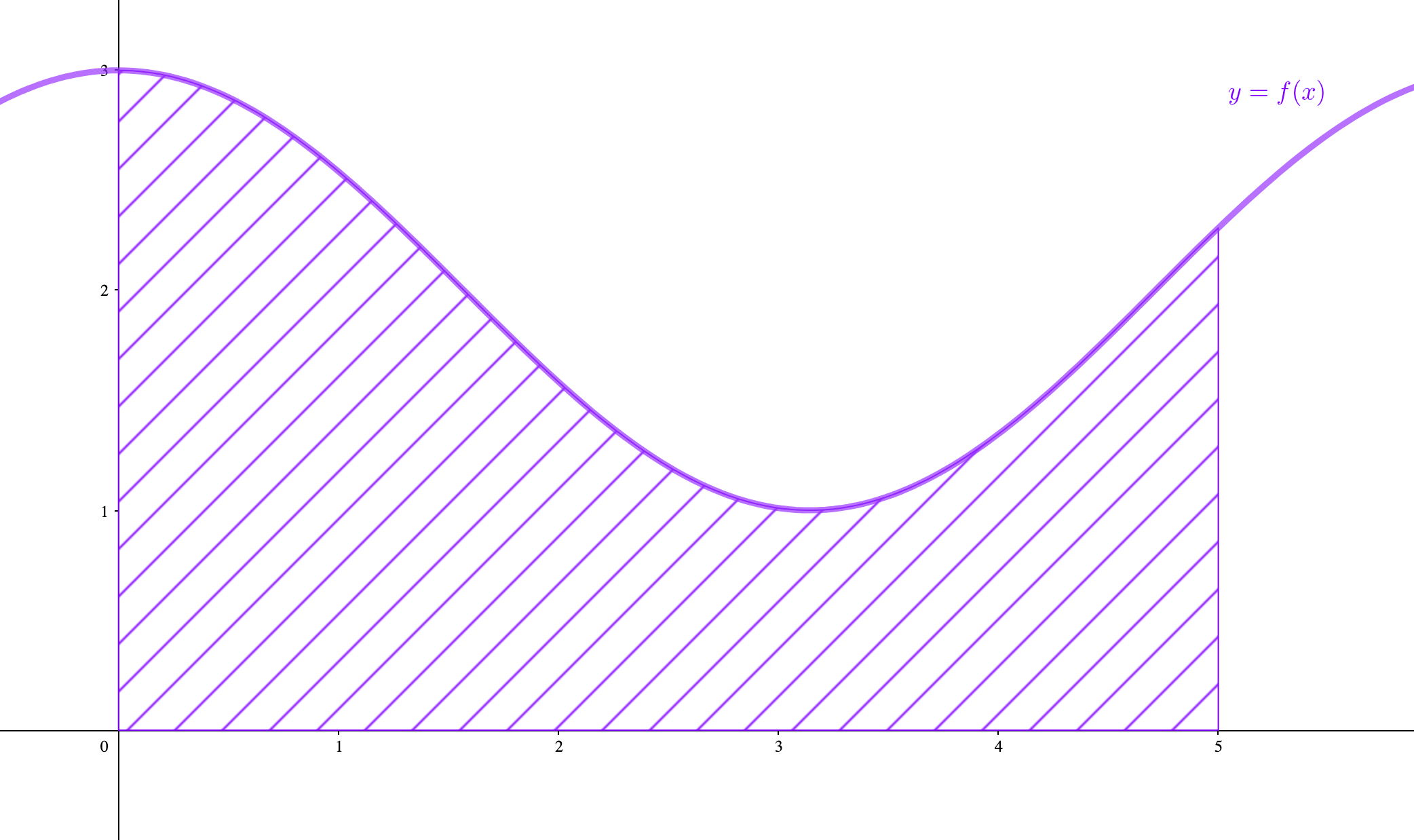
単位正方形を用いて、斜線部の面積を求めてみようとすると。。。

楓

赤色の単位正方形だけだと、隙間があるね。

でも緑色の単位正方形まで足しちゃうと、斜線部の面積よりも大きくなるなぁ。。。

小春

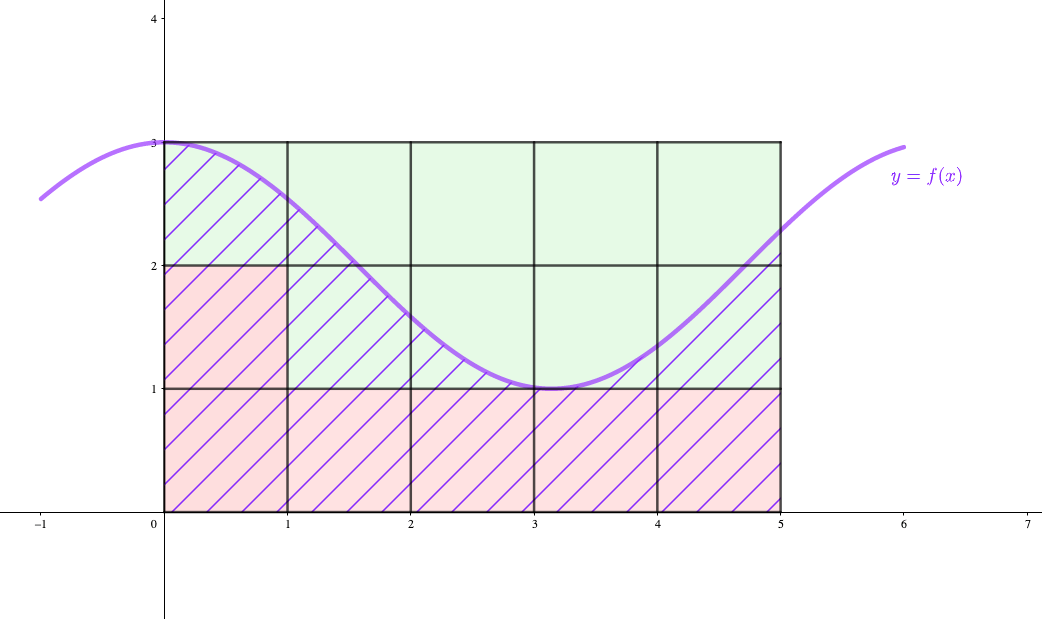
というわけで、これまでのように『単位正方形いくつ分か』だけでは求めることができません。

そこで”面積”の捉え方を、変える必要があるわけです。

面積を求める発想｜無限個の長方形で刻む

そこで次は、正方形ではなく長方形で考えてみることにしましょう。

区間\(0≦x≦5\)の曲線\(f(x)\)が\(x\)軸と作る面積を、長方形に分割して表してみることにします。

楓

ただし、どの長方形も幅は同じとします。

この分割方法だと、長方形の面積の和の方が小さくない？

小春

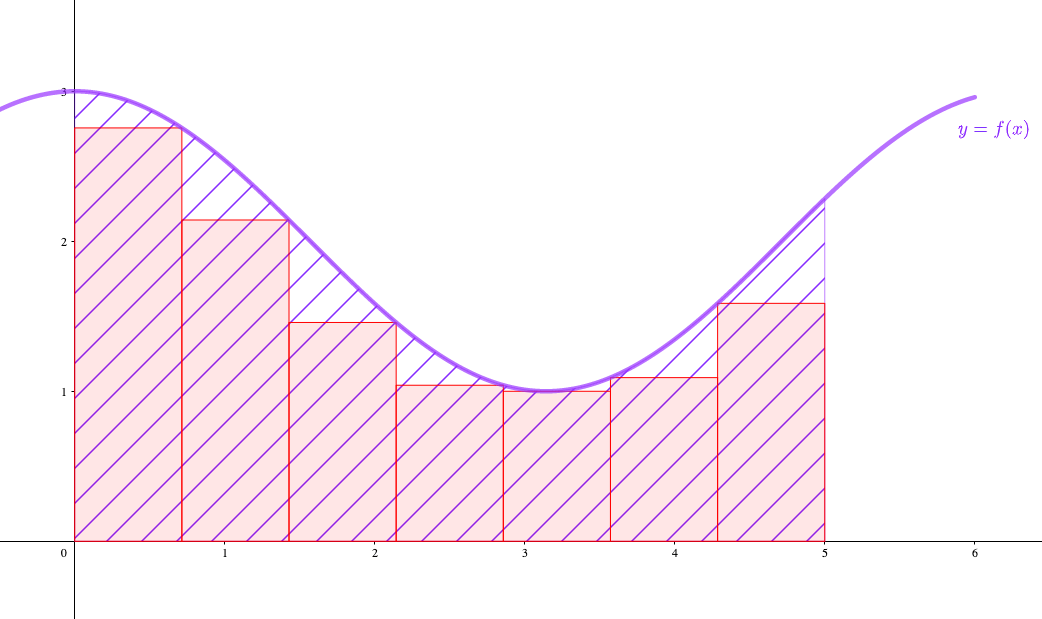
では\(0≦x≦5\)区間の面積を、50個の長方形で分けてみるとどうでしょうか。

楓

より曲線の作る面積に近づいたね。

でもまだ曲線の面積よりも小さいじゃん。

小春

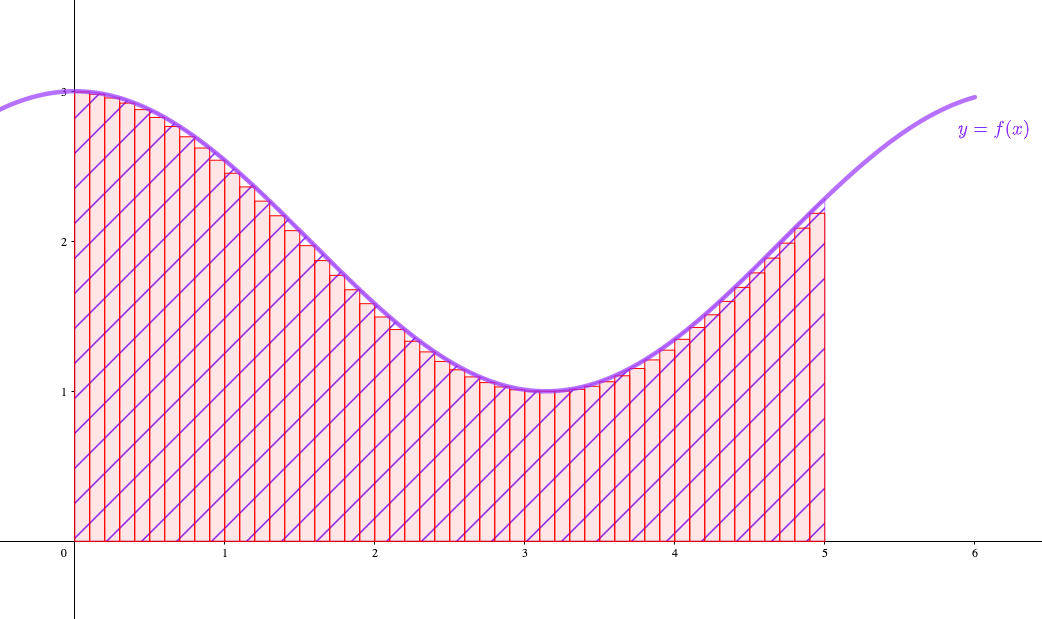
では、200個に分割してみましょう。

小春

こ、これは・・・。ほぼ曲線の作る面積と同じ・・・。

つまり細かく分割するほど、曲線の面積に近くなるってことがわかるね。

楓

区分求積法

ここで長方形の面積について考えてみましょう。

関数\(f(x)\)は、\(x=a\)のとき\(y\)座標を\(f(a)\)と表すことができました。

区間\(0≦x≦5\)を、適当な長さ\(h\)で等分すると、図のように考えることができますね。

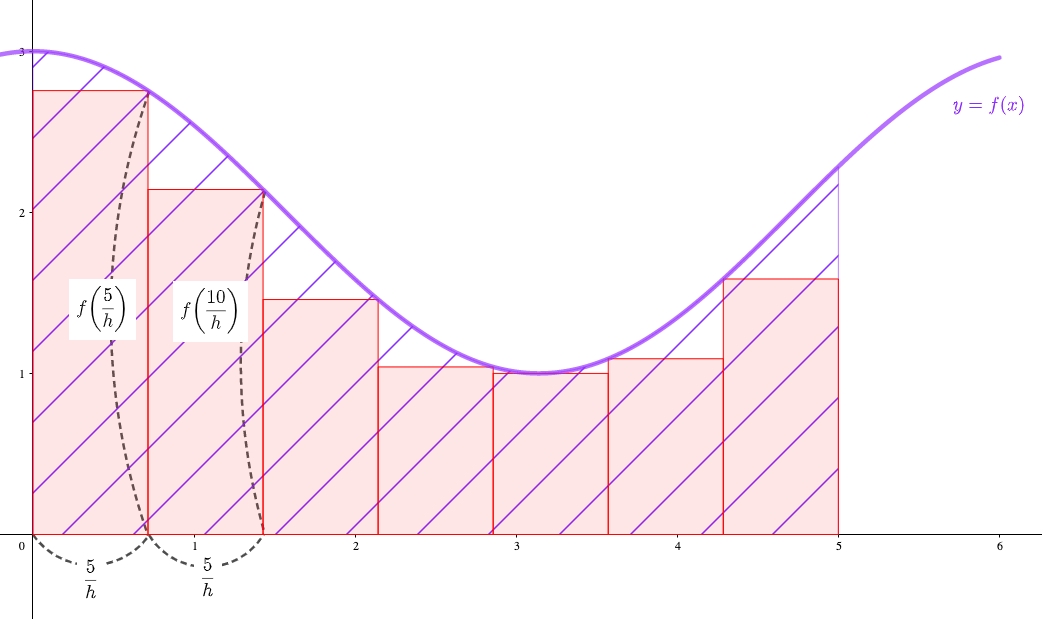
長方形1つの面積はタテ\(\times\)ヨコなので、

と考えられます。

長方形は\(h\)本できるので、それら全ての面積をシグマを使って表すと

となりますね。

\(h\rightarrow \infty\)とすると、幅\(\frac{5}{h}\)がほぼ0に近いような細い長方形、つまり無限本の長方形に分割できます。

200本の長方形に分けただけでもほぼ曲線の面積に近かったのですが、無限本に分割すれば、曲線の面積に究極的に近くなるというわけです。

つまり

は、区間\(0≦x≦5\)における関数\(f(x)\)と\(x\)軸で囲まれた面積を表していると考えてOKというわけ。

まとめると、このような見方をしているわけです。

ただ毎回このように記述するのは面倒ですし、数学アレルギーの人は3時間ぐらい嘔吐してしまいます。

そこで、

とちょっとだけ簡単に表現するようにしました。

楓

\(\int\)をインテグラルと言いますが、これは\(\sum\)（シグマ）のSを縦に伸ばしたものだよ。

積分って、分けて積むって意味なんだね。

小春

つまり

 $$\Large{\underbrace{\int_0^5 \underbrace{f(x)\underbrace{dx}_{\color{red}{ヨコ}}}_{\color{blue}{タテ\times ヨコ}}}_{0≦x≦5区間の長方形の総和}}$$

というわけです。

ちなみに\(dx\)のように、\(d\)がつくものは一般的に『限りなく0に近い』を意味します。

積分の計算方法の発見

楓

ここでは一旦、積分計算を知らないものだと思ってみて欲しい。

この『無限個の長方形を足すことで曲面の面積を求めよう』という考え方は、紀元前の頃からありました。

しかし、

と表せたところで、面積が求められなければただのニックネームにすぎません。

それから長い時を経て、1600年代になりついにこの計算方法が確立されます。

それはとんでもなくぶっ飛んだことの発見につながりました。

区間が\(p\)から\(x\)までの面積を考えてみましょう。ここでは、

と表します。

区間が\(h\)だけ伸びた\(p\)から\(x+h\)までの区間において、面積の変化量を考えてみます。

楓

面積がどれだけ増えたかは、\(F(x+h)-F(x)\)で表せるね。

これまでの流れで行くと、増加分\(h\)の値が小さいほど、増加する面積は長方形と同じとみなせるようになります。

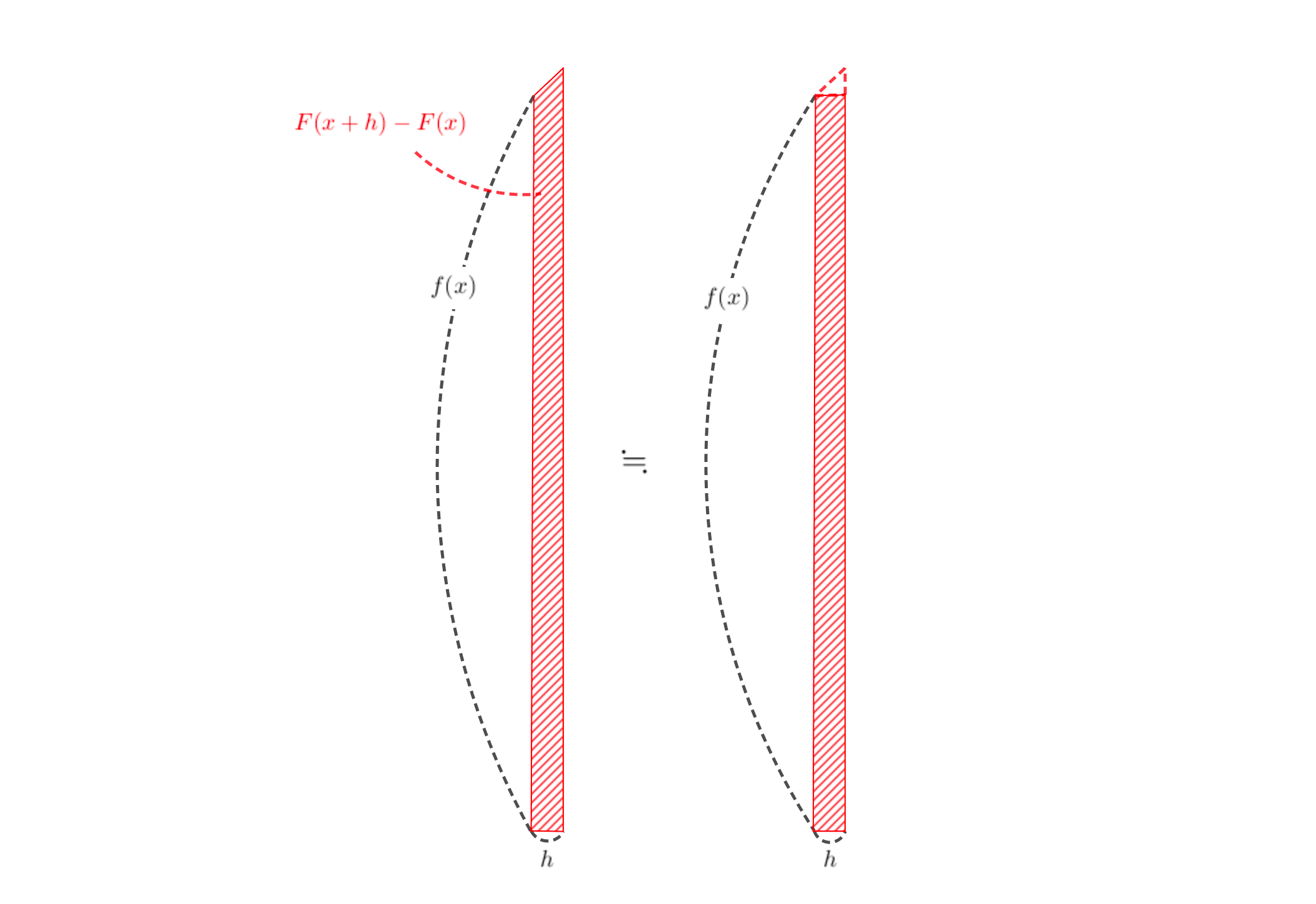
そこで、\(h\)が超小さいと仮定して、面積の増加量分が長方形の面積分程度だとすると、

と考えられます。

このときはまだ、\(h\)が超小さいと仮定しているだけ。

これをさらに細かくするために\(h\rightarrow 0\)としてあげます。

すると、面積の増加量分と、長方形の面積は同じ（とみなすことができるよう）になります。

ここで両辺に\(\frac{1}{h}\)をかけましょう。

すると、

となります。

小春

あ、あれ！？これって、微分じゃない！？

よく気がついたね。その通り、左辺は微分の定義そのものだよ。

楓

なんと色々試行錯誤した結果、面積\(F(x)\)を微分すると曲線の関数\(f(x)\)になることがわかりました。

3に2足して2引くと、3に戻る。

4に5かけて5割ると、4に戻る。

それと同じように、\(f(x)\)を積分した\(F(x)\)を微分すると、\(f(x)\)に戻るというわけです。

楓

この\(F(x)\)を原始関数と言うんだったね。

つまり

ということがわかりました。

以上のことから、

とそれぞれ別々に発展していきました。

まとめ

楓

お疲れ様、まとめをします。

高校数学の教科書では、よくこの原理原則がぶっ飛ばされたまま、積分がただの計算問題となり果てます。

数百年の時を経て発見された『積分は微分の逆演算』という最強の法則が、これからどんどん発展していきます。

楓

面積を求める、ということで始まった積分。それがどんどんいろんなことに使えることがわかっていくよ。

へええ。

小春

また数Ⅲでは、この区分求積法を利用して極限の問題に応用したりすることも可能です。

まずは区分求積法が何を意図しているのかを、じっくり味わってみてください。

今日はここまで、以上「積分の本質について」でした。