【定積分】絶対間違えない計算方法を解説。不定積分と比較すると、正体がわかる。

Today's Topic

$$\int_a^b f(x) dx = F(b)-F(a)$$

楓

さて、今日は積分の計算法則の最後、定積分を扱うよ！

不定積分と同じ積分なの？

小春

楓

計算のプロセス自体はほとんど同じ、だけど定積分は面積を表しているなど、ちょっと違うところもある。

なるほど、じゃあ今日は不定積分との違いに着目したポイントと教えて欲しいな。

小春

この記事を読むと、この意味がわかる！

定積分と不定積分の違い
定積分の意味しているもの

楓

最後に練習問題もあるよ！

Contents

1 定積分とは
2 定積分の解き方
- 2.1 STEP1. 不定積分を解いて、原始関数を見つける
- 2.2 STEP2. 原始関数に代入する
3 定積分の意味
4 まとめ

定積分とは

まずは不定積分から考えていきます。

関数$x^2$の原始関数は、全て

$$\int f(x) dx = \frac{1}{3}x^3 +C$$

という形で表すことができました。

一般に定数部分$C$がどんな数でもOKなので、不定積分によって求めた原始関数は無数に定まることになります。

楓

$\frac{1}{3}x^3+100$も$\frac{1}{3}x^3-\frac{71}{34}$も、微分すると$x^2$になるよね！

では原始関数$F(x)=\frac{1}{3}x^3+C$について、$F(3)-F(1)$の値はどうなるか考えてみましょう。

\begin{align} F(3)-F(1) &= \left(\frac{1}{3}\times 3^3 +C\right)-\left(\frac{1}{3}\times 1^3 +C\right)\\\ &= \frac{26}{3}\\\ \end{align}

（※見切れている場合はスクロール）

小春

あ、積分定数$C$が消えた！

つまりこの解は1通りに定まるってことだね。

楓

このように、関数$f(x)$の原始関数の1つである$F(x)$に対し、適当な値$a,b$を用いた

$$F(b)-F(a)$$

は、どんな原始関数$F(x)$を選んでも、$C$が相殺そうさいするため1つに定まります。

不定積分の解は無数に定まるのに対して、$F(b)-F(a)$の値は1つに定まる特殊性から、

$$\int_a^b f(x) dx = F(b)-F(a)$$

と表現することにし、これを定積分と呼ぶようになりました。

またこのときの$a$を下端かたん、$b$を上端じょうたんといいます。

加えて、数学では

$$F(b)-F(a)=\left[F(x)\right]_a^b$$

のように表すことが多々ありますので、覚えておきましょう。

定積分の解き方

ここでは定積分の解き方を、紹介します。

「もう、こうやれば解が求められるよ」と言えるくらい、簡単な手順に落とし込んだので参考までに。

例題

$$\int_0^2 7x^3 dx$$

STEP1. 不定積分を解いて、原始関数を見つける

定積分の定義を見ても分かるとおり、原始関数$F(x)$が見つからなければ何も始まりません。

そこでまずは、不定積分

$$\int 7x^3 dx$$

を解きます。

不定積分の解き方で紹介した手順通りにやります。

STEP1

原始関数を適当に見つける

微分して$7x^3$に近い形になるものを探します。
今回は$x^4$が当てはまりそうです。
STEP2

係数の調整

ところが、$x^4$は微分すると$4x^3$となります。
$7x^3$と見比べると、$\frac{7}{4}$倍してあげれば良さそうです。
STEP3

積分定数をくっつける

最後に積分定数を忘れずにくっつけて
$$\int 7x^3 dx = \frac{7}{4}x^4 +C$$

楓
最後に$\frac{7}{4}x^4$を微分して$7x^3$になることを確認しておこう！

STEP2. 原始関数に代入する

求めた原始関数$F(x) = \frac{7}{4}x^4 +C$に上端2、下端0を代入すればおしまいです。

\begin{align} \left[ F(x) \right]_0^2 &= F(2)-F(0)\\\ &= \left( \frac{7}{4}\cdot 2^4 + C\right)-\left(\frac{7}{4}\cdot 0^4 +C\right)\\\ &=28\\\ \end{align}

（※見切れている場合はスクロール）

積分定数$C$は消えることがわかっているので、書かなくてもOKです。

定積分の意味

さて、ここまで考えてきた定積分には大きな意味があります。

「不定積分は微分の逆の演算である」という位置付けでしたが、定積分には面積という意味合いが出てきます。

もっと詳しく紹介すると、定積分

$$\int_0^3 x^2 dx$$

は下の図の斜線部の面積を求めることができます。

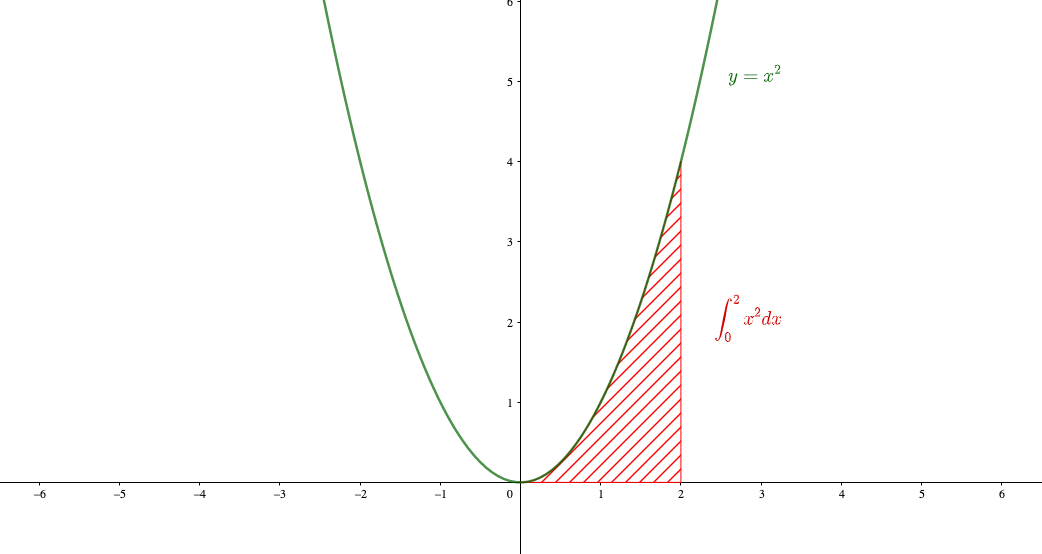
この理由については、こちらの記事で詳しく解説しますね。

: 【区分求積法】なぜ定積分は面積を表すの？文理どっちでも理解できるよう優しく解説

続きを見る

まとめ

楓

最後にまとめるよ！

まとめ

定積分の値を求めるためには、

不定積分を解き、原始関数を適当に1つ求め、
上端と下端の値を代入して、引けば良い。

不定積分は無数の解が定まるが、定積分は唯一1つに定まる。

不定積分は微分の逆演算、定積分は面積という意味合いが強い。

定積分は不定積分とあまり変わらない手法で求められますが、意味合いは若干異なります。

まずはしっかり計算できるようになり、その上で意味を理解すると理解度が早いと思います。

まずは計算問題に取り組んで、計算に慣れるのがベストですよ！

以上、「定積分について」でした。

チェック問題

例題

$$\int_1^3 2x^3 dx$$

（解答）

まずは不定積分

$$\int 2x^3 dx$$

から考えます。

微分して$x^3$になるような関数は$x^4$が当てはまります。

$(x^4)'=4x^3$より、係数を見比べると$\frac{1}{2}$倍してあげれば良さそうです。

よって、

$$\int 2x^3 dx=\frac{1}{2}x^4 +C$$

これにより、

\begin{align} \int_1^3 2x^3 &= \left[\frac{1}{2}x^4\right]_1^3\\\ &= \frac{1}{2}\left(3^4 - 1^4\right)\\\ &= 40 \end{align}

例題

$$\int_2^3 (x^2-x+1)dx$$

（解答）

まずは不定積分

$$\int (x^2-x+1)dx$$

を求めましょう。

不定積分の計算法則から、

\begin{align} \int (x^2-x+1)dx &= \int x^2 dx-\int x dx + \int dx\\\ &= \frac{1}{3}x^3 -\frac{1}{2}x^2 +x +C\\\ \end{align}

（※見切れている場合はスクロール）

よって、

\begin{align} \int_2^3 (x^2-x+1)dx &= \left[\frac{1}{3}x^3 -\frac{1}{2}x^2 +x\right]_2^3\\\ &= \left(\frac{1}{3}\cdot 3^3 -\frac{1}{2}\cdot 3^2 +3\right)-\left(\frac{1}{3}\cdot 2^3 -\frac{1}{2}\cdot 2^2 +2\right)\\\ &= \frac{29}{6} \end{align}

（※見切れている場合はスクロール）

気付いたかもしれませんが、不定積分の計算法則と同様に、定積分のインテグラルでも「インテグラルの分配法則」が成り立ちます。

これについては、こちらの記事で解説します。