【囲まれた面積】定積分で求めるときに持っていたほうがいいイメージをささっと解説

Today's Topic

$$S=\int_a^b \left(f(x)-g(x)\right)dx$$

小春

楓くん、2つの曲線で囲まれた面積ってどうして引き算で求められるの？

簡単にいうと「大きい面積」ー「小さい面積」をしているからなんだ。

楓

小春

なんか図で見せてくれない・・・？

じゃあ今日は囲まれた面積の求め方のコツと、定積分の捉え直しをやってみようか。

楓

この記事を読むと、この意味がわかる！

囲まれた面積を求める際に必要なイメージ
$x$軸と曲線で囲まれたグラフの考え方

楓

最後に練習問題もあるから、やってみよう！

Contents

1 2つのグラフで囲まれた面積
2 $x$軸との面積
- 2.1 $x$軸よりも上のグラフ
- 2.2 $x$軸よりも下のグラフ
3 まとめ

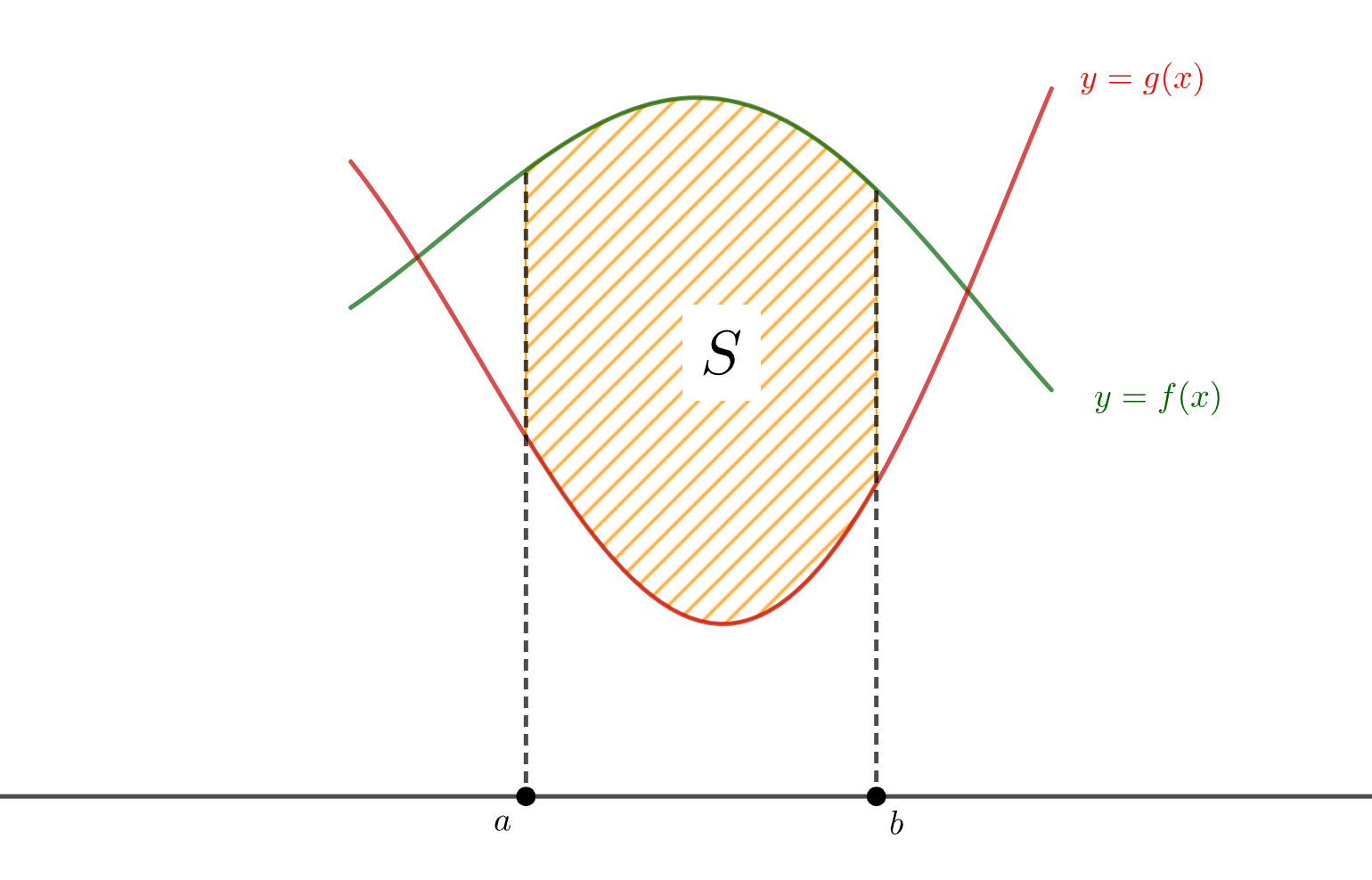
2つのグラフで囲まれた面積

2つのグラフで囲まれた図形の面積を考えるためには、まずそれぞれの面積を求めるところから始めます。

STEP1. $f(x)$が$a≦x≦b$で作る面積

定積分が面積を表す理由で紹介した通り、一般に

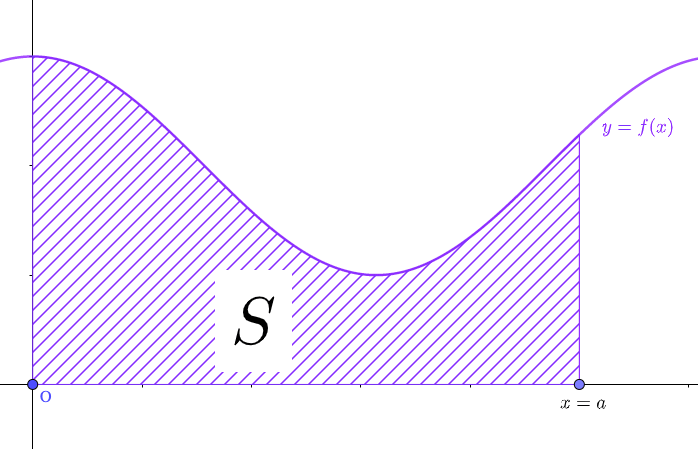
$$S=\int_0^a f(x) dx$$

が成り立ちます。

これをもとに考えると、

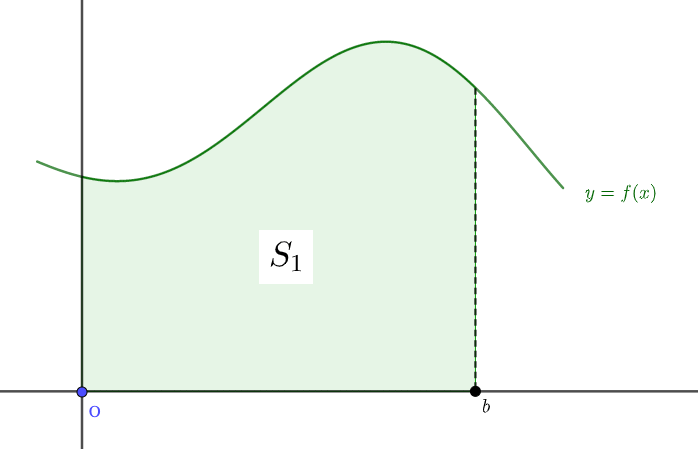
$$S_1 = \int_0^b f(x) dx$$

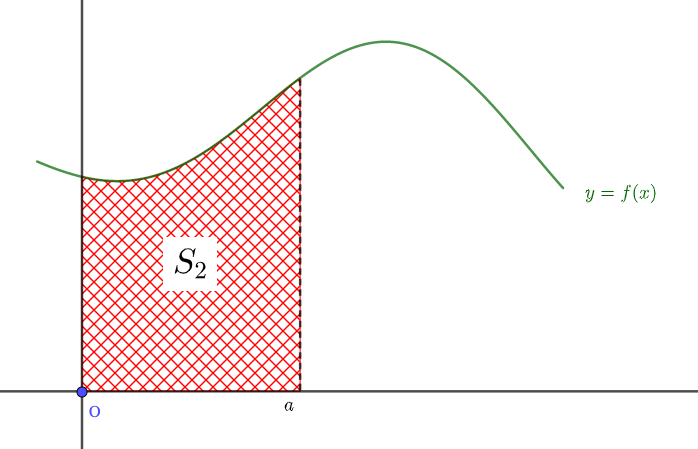
$$S_2 = \int_0^a f(x) dx$$

の2つから、$f(x)$が$a≦x≦b$で作る面積$S_f$は

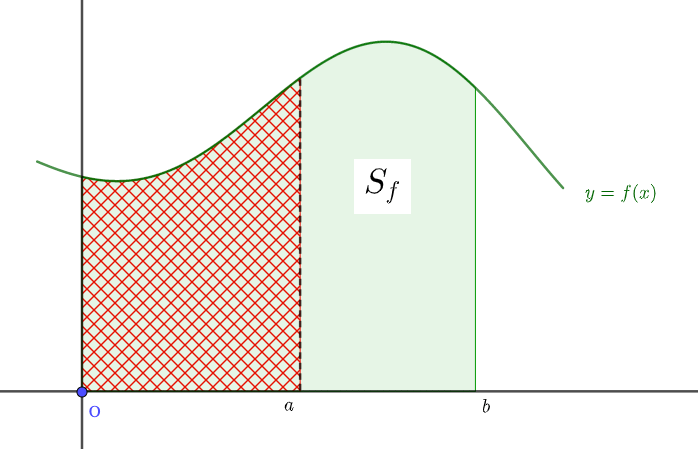
$$S_f = \int_0^b f(x) dx - \int_0^a f(x) dx$$

で求められることがわかります。

また、定積分の計算公式から

\begin{align} S_f &= \int_0^b f(x) dx - \int_0^a f(x) dx\\\ &= \int_0^b f(x) dx + \int_a^0 f(x) dx\\\ &= \int_a^b f(x) dx\\\ \end{align}

とまとめられることもわかります。

STEP2. $g(x)$が$a≦x≦b$で作る面積

$g(x)$が$a≦x≦b$で作る面積を$S_g$とします。

$f(x)$が作る面積$S_f$と同様に考えると、

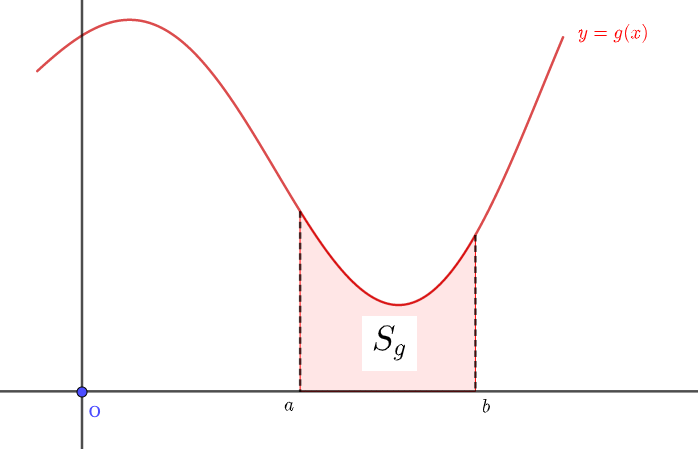
$$S_g = \int_a^b g(x) dx$$

となりますね。

STEP3. 大きい面積ー小さい面積

見た目で分かる通り、$S_f$の方が$S_g$よりも大きくなりますね。

よって区間$a≦x≦b$において$f(x)$と$g(x)$で囲まれた面積$S$は

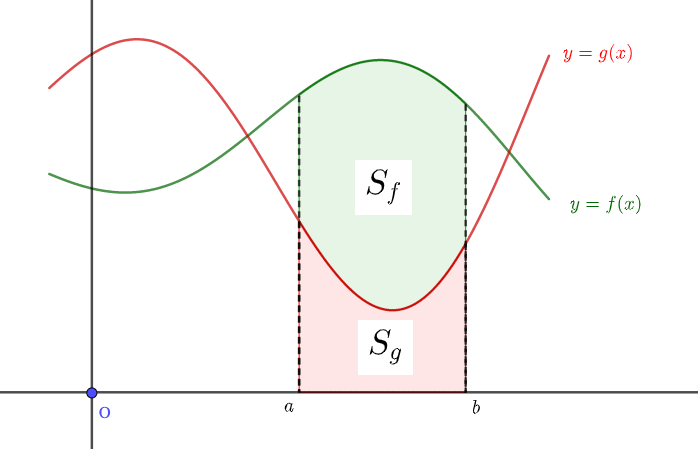
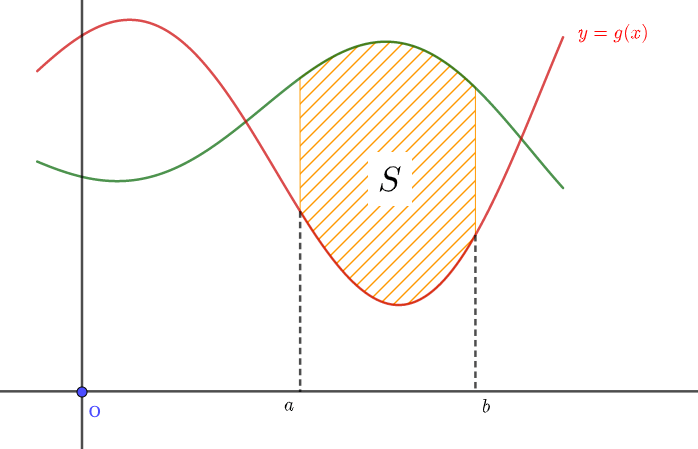
$$S = S_f - S_g $$

で求められます。

インテグラルの式に直して考えてみると、定積分の計算法則より次のような変形ができます。

\begin{align} S &= S_f-S_g\\\ &= \int_a^b f(x) dx - \int_a^b g(x) dx\\\ &=\int_a^b \left(f(x)-g(x)\right)dx \end{align}

小春

要は上側にある$f(x)$から下側にある$g(x)$を引いたものの積分をすればいいんだね！

$x$軸との面積

以上のように、区間$a≦x≦b$における2つのグラフで囲まれた面積は

$$\int_a^b \left((上側のグラフ) - (下側のグラフ)\right)dx$$

と考えることができるので、次のように考えることができます。

$x$軸よりも上のグラフ

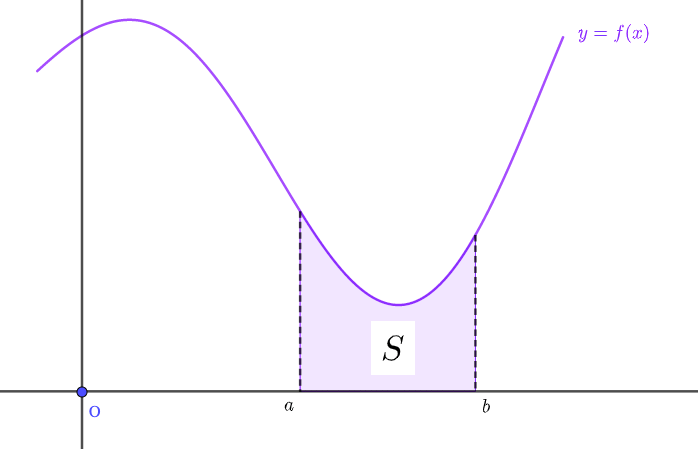
上のような図の場合、$x$軸の方が$y=f(x)$よりも下にあります。

この面積$S$は、$x$軸は$y=0$と表すことができたので、

$$\int_a^b \left(\underbrace{f(x)}_{上のグラフ} - \underbrace{0}_{下のグラフ} \right)dx$$

（※見切れている場合はスクロール）

と考えることができます。

$x$軸よりも下のグラフ

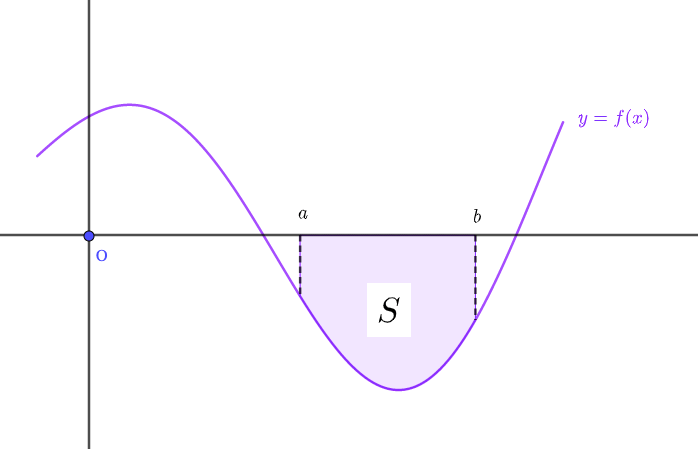
上のような図の場合、$x$軸の方が$y=f(x)$よりも上にあります。

この面積$S$は、$x$軸は$y=0$と表すことができたので、

$$\int_a^b \left( \underbrace{0}_{上のグラフ}-\underbrace{f(x)}_{下のグラフ} \right)dx$$

（※見切れている場合はスクロール）

と考えることができます。

まとめ

楓

今日はこれだけ！まとめるよ！

まとめ

2つのグラフで囲まれる面積を求めるためには、その区間で上にあるグラフ$y=f(x)$と下にあるグラフ$y=g(x)$に着目して、『$f(x)$が$x$軸と作る面積』ー『$g(x)$が$x$軸と作る面積』を考えればOK。
この計算は$$\int_a^b \left(f(x)-g(x)\right)dx$$のようにまとめることができる。

この大きい面積から小さい面積をひく、といういっけん簡単に聞こえる当たり前の行動。

このイメージがあるかないかで計算スピードが大きく変わります。

練習問題などでも、ぜひ「どの面積からどこを引いているのかな？」と考えてみて下さい。

以上、「囲まれた面積の求め方について」でした。

チェック問題

例題

2つの放物線$y=x^2-2x,\ y=-x^2+3x$と直線$x=1,\ x=2$で囲まれた部分の面積$S$を求めよ。

（解答）

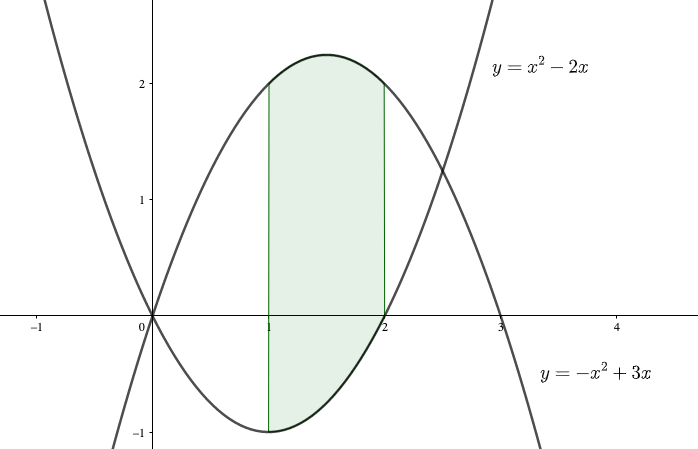
グラフを考えてみると、区間$1≦x≦2$では$y=-x^2+3x$の方が上に位置する。

よって、

\begin{align} S &= \int_1^2 \left(\left(-x^2+3x\right)-\left(x^2-2x\right)\right)dx\\\ &= \int_1^2 \left(-2x^2+5x\right)dx\\\ &=\left[-\frac{2}{3}x^3+\frac{5}{2}x^2\right]_1^2\\\ &= \frac{17}{6}\\\ \end{align}

（※見切れている場合はスクロール）

例題

3次関数$y=x^3-3x^2+2x$が区間$0≦x≦2$において、$x$軸となす面積$S$を求めよ。

（解答）

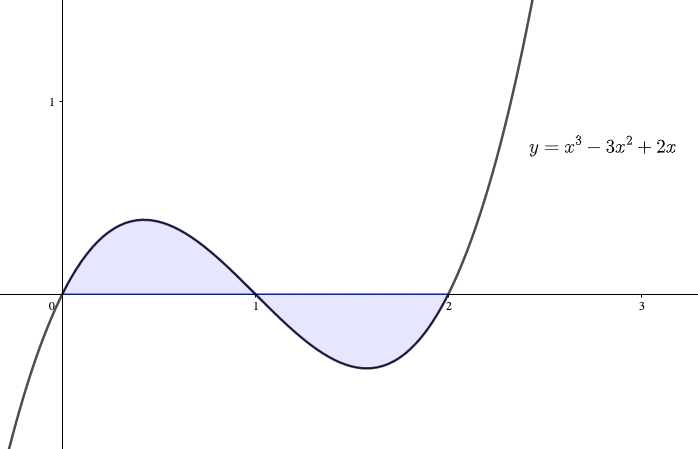
グラフを考えると、

区間$0≦x≦1$では曲線のほうが、$x$軸よりも上に位置している
区間$1≦x≦2$では曲線のほうが、$x$軸よりも下に位置している

ことがわかる。

なので、区間ごとに分けて

\begin{align} S &= \int_0^1 \left(f(x)-0\right)dx + \int_1^2 \left(0-f(x)\right)dx\\\ &= \left[\frac{1}{4}x^4-x^3+x^2\right]_0^1-\left[-\frac{1}{4}x^4+x^3-x^2\right]_1^2\\\&=\frac{1}{2}\\\ \end{align}

（※見切れている場合はスクロール）