Today's Topic
対数関数を考えるためには、底の条件・真数条件を最初に確認し、得られた解がその条件から得られた不等式・方程式にマッチするかを確認すれば良い。




この記事を読むと、この問題が解ける!
- $$\log_{\frac{1}{2}} \left(2x-\frac{1}{8}\right) > 3$$
- $$\log_{3}(5-x) - \log_3(3x+1) = 0$$

Contents
底の条件・真数条件
対数関数は、次のように定義されていました。
定義
\(a \neq 1,\ 0 < a,\ x>0\)とする。この\(a\)を底に持つ対数で表される関数
$$y = \log_a x$$
を対数関数という。
参考【対数関数の定義と性質】グラフからわかる重要性質と問題への使い方を徹底解説!
この定義において、底\(a\)には\(a \neq 1,\ 0 < a\)という条件が設けられます。
これを底の条件と呼びます。
同様に真数\(x\)にも\(x > 0\)という条件が設定されています。
これを真数条件と呼びます。
どちらも対数関数を考える上では必須の条件なのですが、そもそもなぜこの条件は必要なのでしょうか?
結論から言ってしまうと、そのほうが『人間の感覚にマッチした数学的に都合がいいから』です。
底の条件が必要な理由
まずは底の条件から見ていくことにしましょう。
底の条件には\(a \neq 1,\ 0 < a\)という2つの条件が含まれています。
実は、どちらも関数として成立させるためには欠かせないものなのです。
\( a =0, a= 1\)のとき、関数ではなくなる
では条件に一致しない、\(a=0\)のときを考えてみましょう。
\(y = \log_0 x\)は指数関数に直すと\(x = 0^y\)となります。
おやおや、これでは\(y\)にどんな値を取っても、\(x\)の値は常に0になりますね。
さらに\(y= -1\)のような負の値になると、
$$x = 0^{-1} = \frac{1}{0}$$
となり、0で数を割ることはできないのでこの場合は定義できなくなってしまいます。
参考【どんな数も0では割れない】減点されないために知っておきたい分数のワナ。
つまり、\(y=\log_0 x\)は\(x=0,\ y> 0\)を満たす直線ということになりますが、これは関数の定義から関数でないことがわかります。
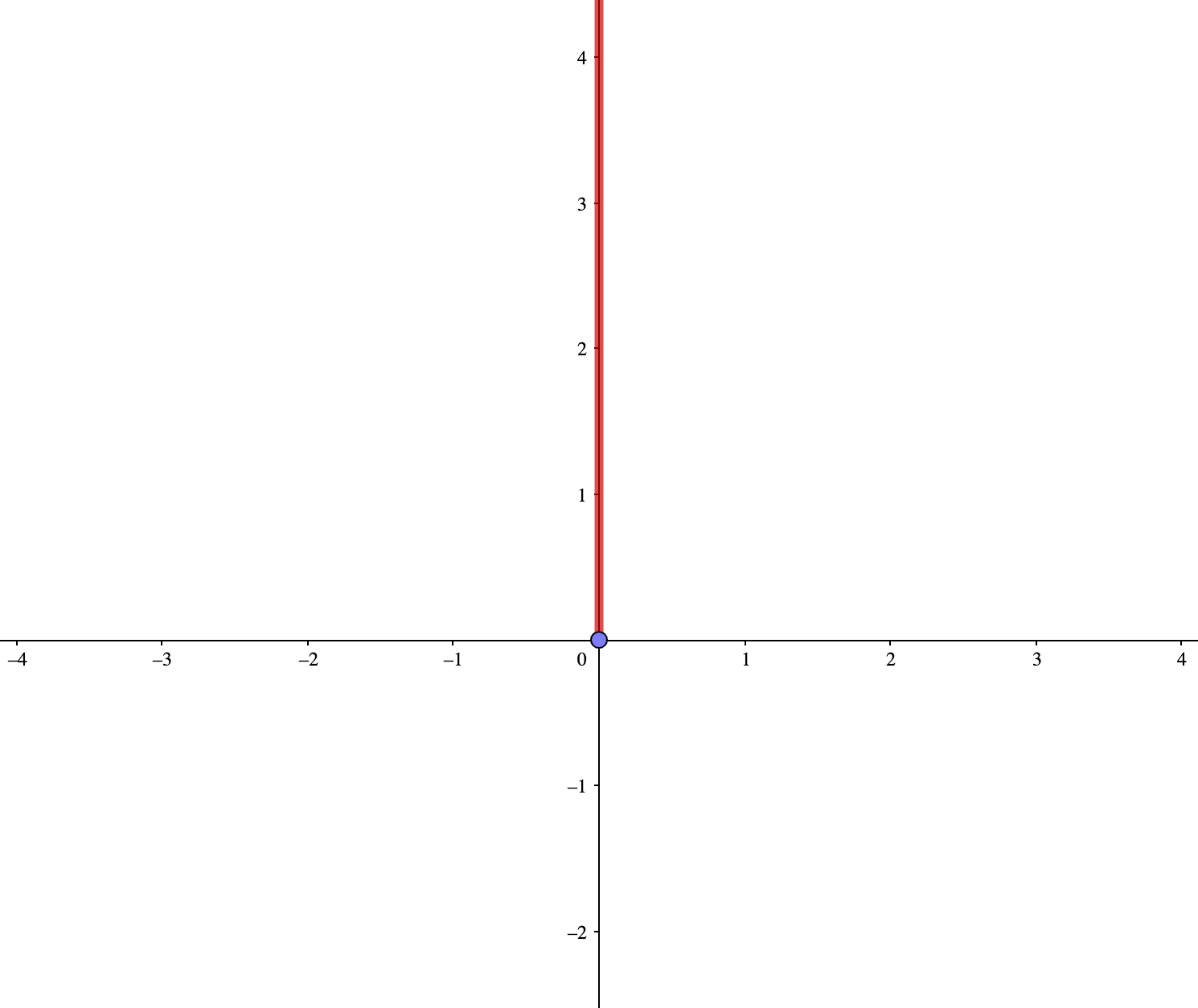
参考【関数とは】中学生でも大丈夫!曖昧にしがちな関数の特徴をしっかりマスターしよう
底\(a=1\)の場合でも同じです。
\(y=\log_1 x\)は指数関数に直すと、\(x = 1^y\)ということになります。
先ほどと違い、\(y\)の値に制限がなくなりましたが、どんな\(y\)の値を取っても\(x\)の値は常に1になります。
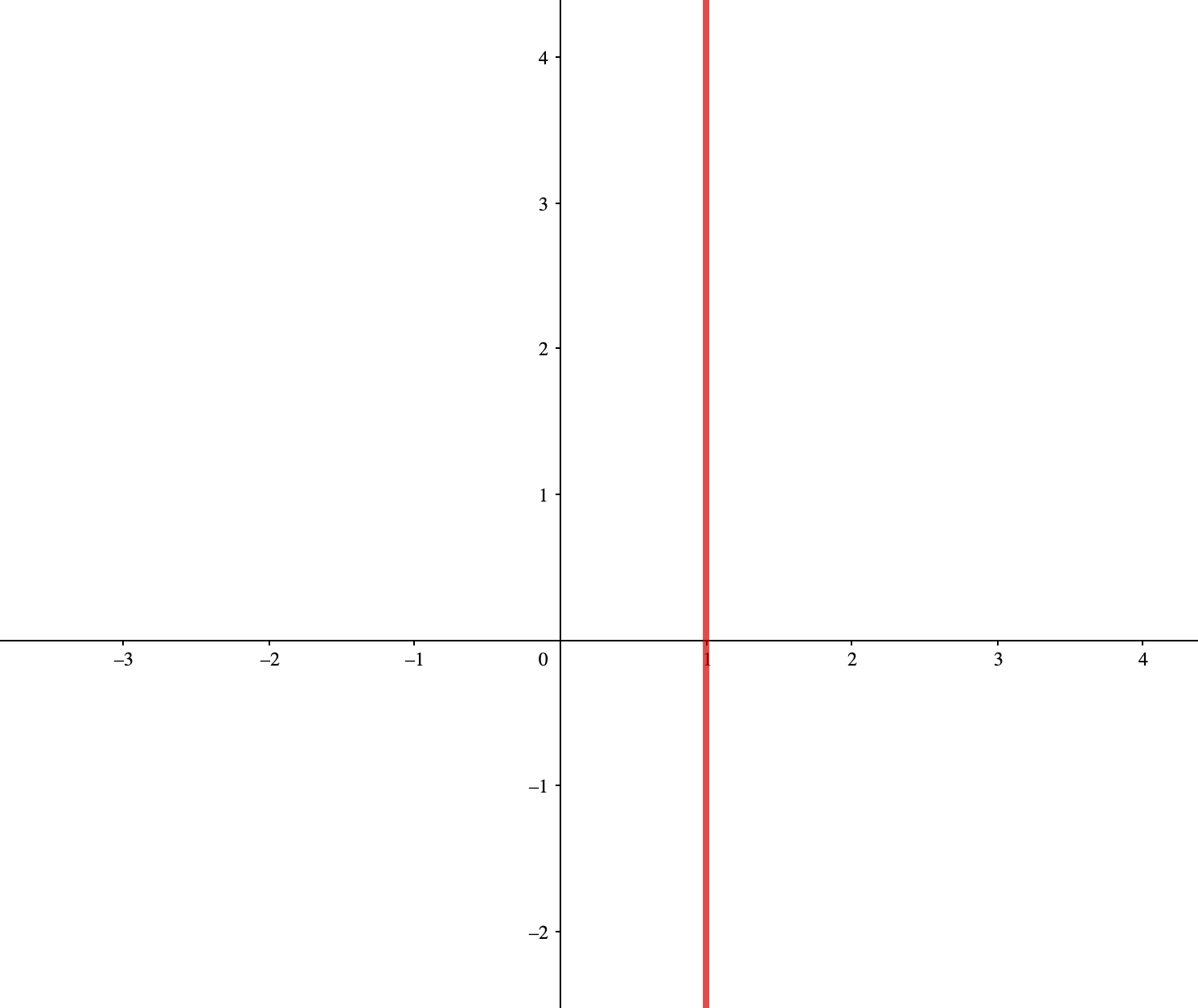
グラフを見てみると一目瞭然ですが、こちらも当然関数ではありません。
よって底の条件がなければ関数として対数関数を定義できなくなることがわかります。
底の条件\(a\neq 0, 1\)がなければ、\(y=\log_a x\)は\(y\)軸と平行な直線になる、すなわち関数ではなくなる。
\( a\)が負だと実関数として考えられなくなる
続いて、具体的に\(a= -2\)の場合を考えて、底の条件\(0 < a\)の必要性を見てみましょう。
\(y = \log_{-2} x\)を指数関数に直すと\(x = \left(-2\right)^y\)となります。
例えば\(y=\frac{m}{n}\)のように、\(y\)が有理数の値を取る場面を考えてみましょう。
すると、指数法則から、
となりますが、\(m\)が奇数の場合、ルートの中身が負になってしまうため、これは実関数では定義できません。
高校までで習うような\(x,y\)の値が共に実数である関数のことを実関数と言います。これを複素数まで拡大する複素関数あれば、底の条件を広げることは可能ですが、高校数学では扱わないので一旦スキップしておきましょう。

仮に指数\(y\)が整数しか取らないと制限をつけてみましょう。
すると、\(y=\log_{-2} x\)は指数関数に直すと、
となり、ちゃんと定義できます。
しかし、
\(y=2\)のとき、\(x=4\)
\(y=3\)のとき、\(x=-8\)
となり、\(xy\)座標ではとても表現しにくい動きをしていることがわかります。
このように不気味な動き&実関数でなくなる可能性がある、なんてとても扱いにくいですね。
よって底は負にならないという条件をつけることで、より有意義な関数の定義に仕上げたというわけです。
底の条件\(0 < a\)がなければ、\(y=\log_a x\)



参考【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから
真数条件が定まる理由
さてお次は真数条件ですが、こちらは底の条件により自動的に決まるものです。
底の条件を満たすとき、対数関数\(y = \log_a x\)は次のようなグラフを描きます。
\(0< a< 1\)のとき
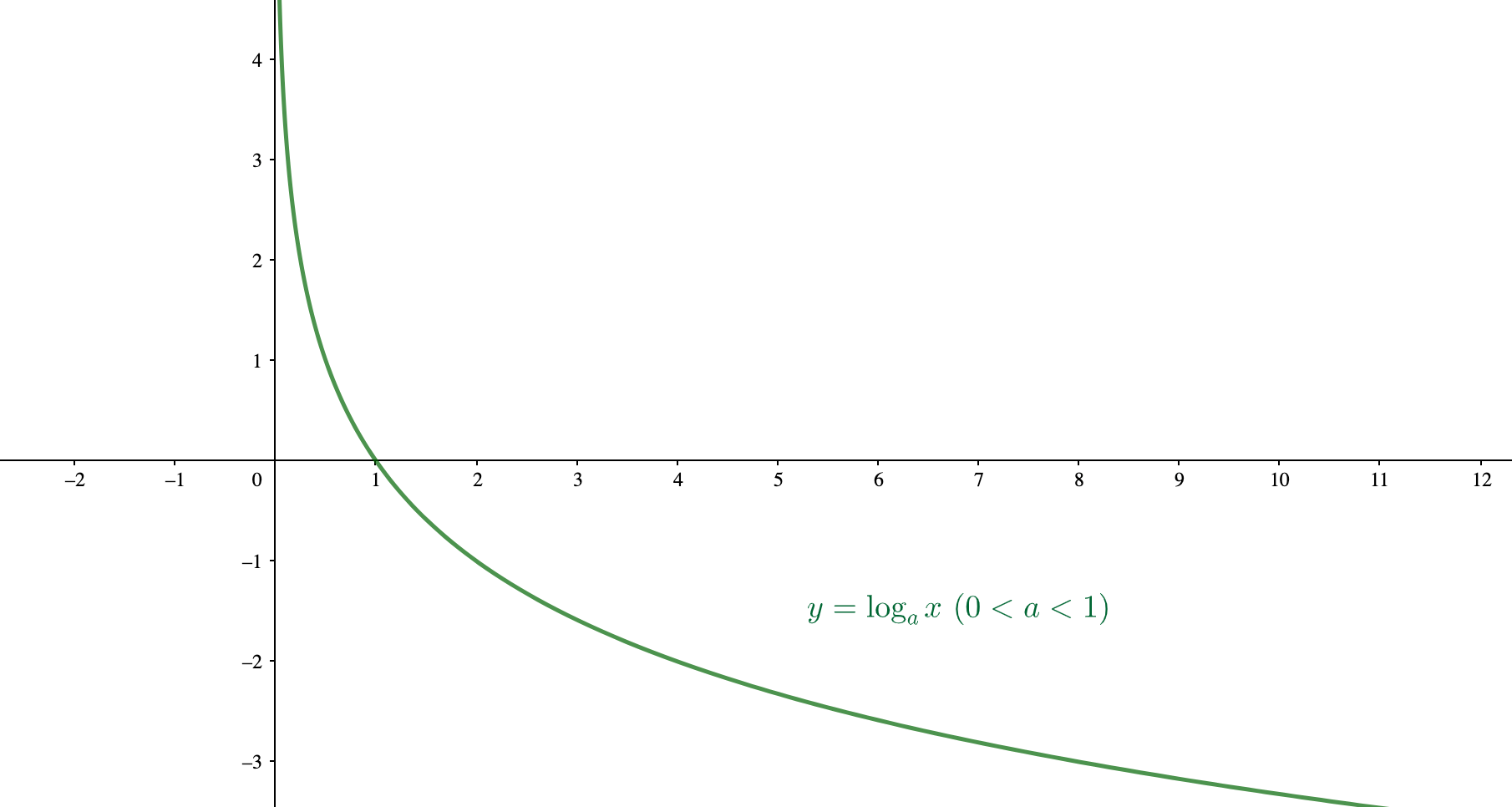
\(0 < a\)のとき
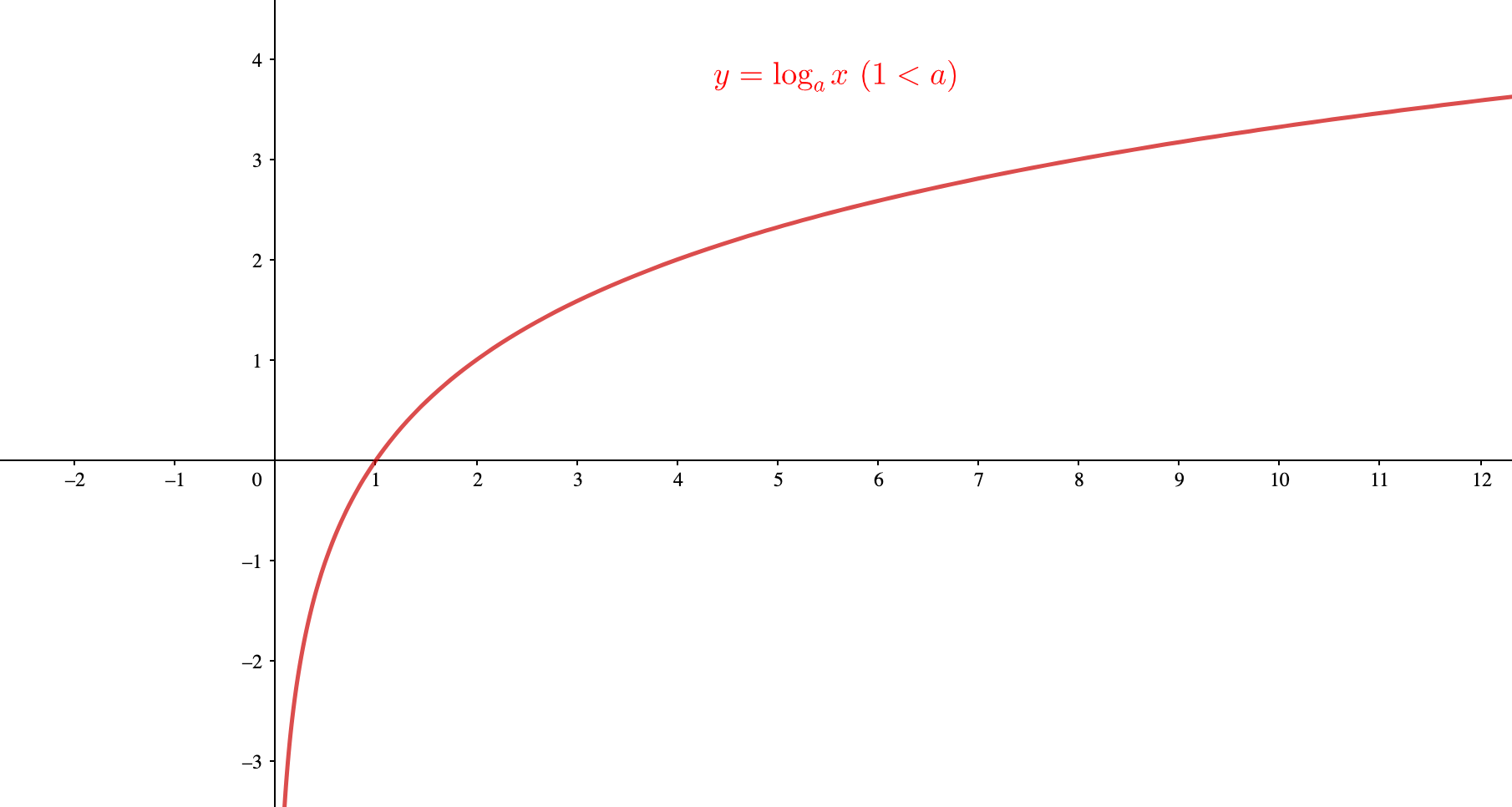
参考【対数関数の定義と性質】グラフからわかる重要性質と問題への使い方を徹底解説!
グラフを見てみると、\(x>0\)であることがはっきりとわかりますね。
つまり
対数関数とは、底の条件\(a\neq 1, 0< a\)を満たす場合にのみ定義することができ、この条件を満たすとき、真数条件\(x>0\)は絶対に成り立っていないとおかしい
ということになります。
底の条件・真数条件をチェックすべきタイミング
さてそんな底の条件・真数条件ですが、対数の問題が出るたびに確認しておくに越したことはありません。
ではどんな場面、どのタイミングで確認しておくべきか見てみましょう。
底の条件をチェックするタイミング
底の条件をチェックすべき状況とは、ずばり底に変数が含まれている場合です。
具体例を見てみましょう。
例題
$$\log_a 81 =-2$$
(解答)
底の条件より\(0<a\)。
与式を指数関数に直すと、\(a^{-2} = 81\)となる。
\(0<a\)なので、\(a=\frac{1}{9}\)。
底に変数が含まれている場合、底の条件を最初に確認して、求められた解が底の条件によって求められた不等式との共通範囲内であるかを考えれば良い。
真数条件をチェックするタイミング
真数条件は、真数に変数が含まれる場合、必ずチェックが必要です。
先ほどの底に変数が含まれる場面とは異なり、この真数条件がマストな場面はかなり多いです。
メモ
なぜ真数条件を確認する場面が多いのか、それは対数の計算法則がそもそも真数条件を前提に構築されていることが原因です。
対数の計算法則
\(a>0,a\neq1,M>0,N>0\)のとき
- \(\log_a MN = \log_a M + \log_a N\)
- \(\log_a\frac{M}{N} = \log_a M - \log_a N\)
- \(\log_a M^r = r\cdot \log_a M\)

参考【対数の計算法則】なぜ掛け算が足し算に?対数の計算は定義を見返そう!
例題
$$\log_2 x ≦ 3$$
(解答)
与式を底が同じ対数で表現すると、\(3 = \log_2 8\)より
$$\log_2 x ≦ \log_2 8$$
底2は1よりも大きいので\(y = \log_2 x\)は単調増加する。
よって\(x\)の値が大きいほど\(y = \log_2 x\)の値も大きくなるので、\(x ≦8\)。
ここで、真数条件より\(x>0\)。
よって共通範囲から
$$0< x ≦ 8$$
もし真数条件を確認していなければ、\(x>0\)という条件は見つからないでしょう。
これが抜ければ解答とは言えなくなります。
真数に変数が含まれている場合、真数条件を最初に確認して、求められた解が底の条件によって求められた不等式との共通範囲内であるかを考えれば良い。
まとめ

まとめ
対数関数を考えるためには、底の条件・真数条件を最初に確認し、得られた解がその条件から得られた不等式・方程式にマッチするかを確認すれば良い。
底の条件は対数関数を考えるために必須となり、真数条件は対数の計算法則を成り立たせる上で必須となります。
そのため、必ず最初に確認しておく必要があり、得られた解がその条件にマッチしているか確認する必要があります。
対数は計算自体は簡単ですが、この2つの条件が思わぬ落とし穴になることがあるので、気を抜かずしっかりと解き切るようにしましょう。
以上、「底の条件・真数条件について」でした。
チェック問題
例題
$$\log_{\frac{1}{2}} \left(2x-\frac{1}{8}\right) > 3$$
真数条件より、
よって\(x > \frac{1}{16}\)。
より
について考えれば良い。
底が1より小さな対数関数は、単調減少するので
であれば良い。
これを整理すると、\( x < \frac{1}{8}\)。
よって
例題
$$\log_{3}(5-x) - \log_3(3x+1) = 0$$
真数条件より、\(5 - x > 0\)かつ\(3x+1 > 0\)。
この共通範囲は、\(-\frac{1}{3}<x<5\)である。
与式は
とできる。
わざわざ対数の計算法則を使って、$$\log_3 \frac{5-x}{3x+1}$$なんてしなくてもOKですよ・・・
よって、
を考えればよく、この解は\(x=1\)。
この解は\(-\frac{1}{3}<x<5\)に当てはまるので、答えは
となる。








