【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

小春

学校で指数関数やったけど、なんかモヤモヤするんだよね・・・。

あ！それ大事！実は指数関数には、みんなスルーしてしまう大事なポイントがあるんだ！

楓

小春

大事なポイント？

そう！それは「指数法則」と「指数関数」にはギャップがあるっていうことなんだけど、それがわかると指数関数の理解が超深まるよ！

楓

小春

つまり指数法則と比較することで、より明確に特徴がわかるようになるのね！

指数関数の定義

楓

一般に指数関数は、次のように定義されます。

この定義だと、

の2通りが考えられますが、

の場合は、指数関数として考えないと言っています。

小春

そもそもなんでこんな定義になっているの？

結論から言ってしまうと、そのほうが『人間の感覚にマッチした数学的に都合がいいから』です。

では指数法則をもとに、指数関数のイメージを身につけていきましょう。

【まえおき】指数法則の妥協

『ナゼ0乗が1になるのか』『ナゼ分数乗がルートになるのか』で解説した通り、高校数学から学ぶ数にはいくつかの妥協が存在します。

その妥協とは、結局のところ、3つの指数法則

を満たすように定義したため、必要になったのでした。

楓

このように、都合の良さを考えて定義することは、多々あるよ。

指数関数が定義できる底の条件

では指数関数が定義できる底の条件と、そのときのグラフについて解説します。

『どんな数\(x\)に対しても、対応する\(y\)の値が存在するかどうか』に着目してみましょう。

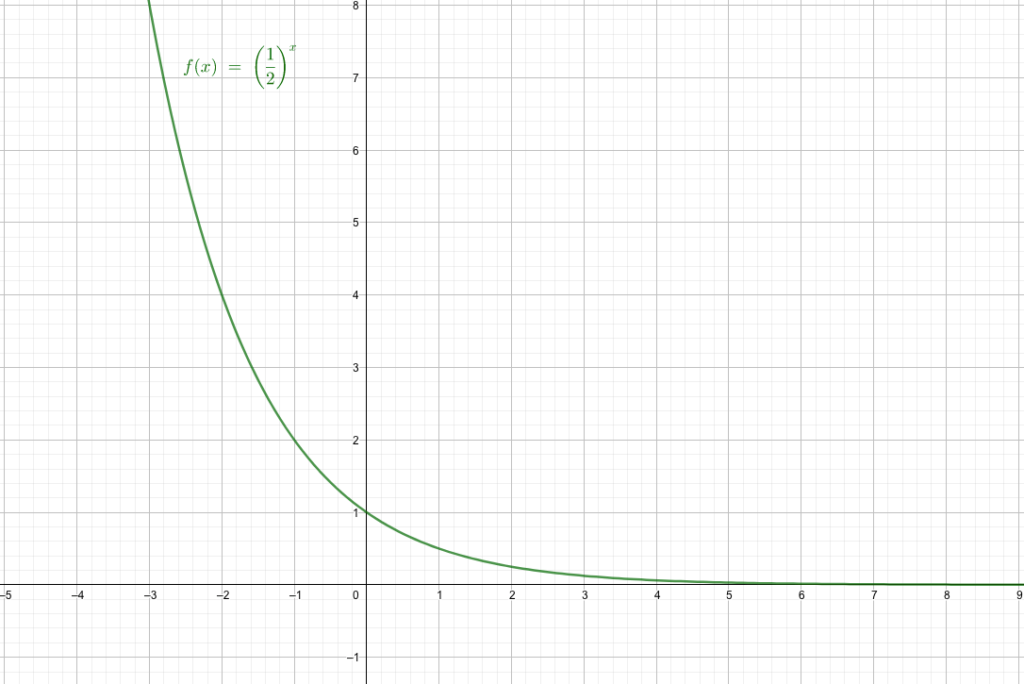
\(0<a<1\)

例として

をみてみましょう。

このとき、実数の指数法則を考えると、どんな実数を\(x\)に当てはめても、必ず対応する\(y\)の値が存在することがわかります。

実際グラフを見てみると、図のような連続な曲線を描いています。

 

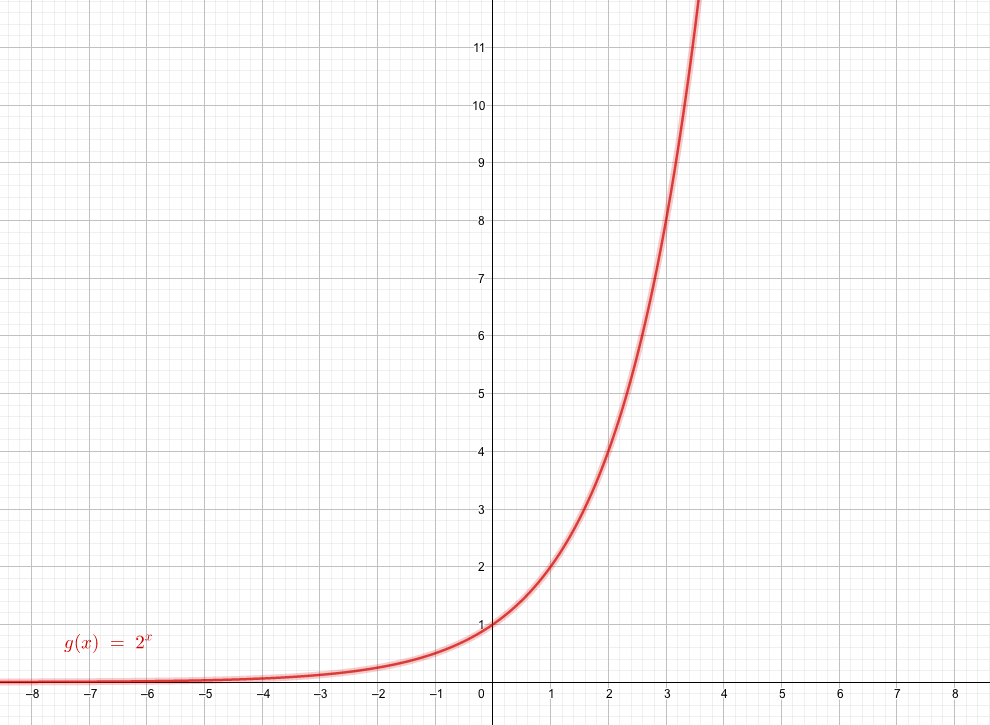
\(1<a\)

例として

をみてみましょう。

実数の指数法則を考えれば、どんな実数を\(x\)に当てはめても、必ず対応する\(y\)の値が存在することがわかります。

グラフは先ほどと同様に連続的な曲線ですが、\(0<a<1\)の場合のグラフとは\(y\)軸対象になっていることが特徴です。

指数関数が定義できてない底の条件

ではここからは、なぜ

の場合は、指数関数として考えないのか、を調べていきましょう。

前提として、関数への理解が必要になります。

関数って何ですか？と聞かれて説明できない方はぜひ復習しておいて下さい。

参考【関数とは】中学生でも大丈夫！曖昧にしがちな関数の特徴をしっかりマスターしよう

aが負のとき定義しない理由

ここでは、指数関数\(y=a^x\)の底\(a\)が負の数、つまり\(a<0\)でもOKだとしてみます。

例として、\(y=\left(-2\right)^x\)のときを考えてみましょう。

例えば、\(x\)が有理数\(x=\frac{m}{n}\)のときを調べると、

となりますね。

具体的に\(n=2, m=1\)のときを考えると、\(y=\sqrt{-2}\)となり考えることができません。

楓

平方根\(\sqrt{k}\)は、必ず\(k≧0\)であるという定義だったね。

なるほど、だから\(a<0\)のとき、有理数における\(y=a^x\)を考えることができないんだね。

小春

ただし、\(x\)が整数のときだけ考えることができます。

例えば\(x=3\)のとき、\(y=(-2)^x=-8\)のように。

でもグラフを調べてみると。。。

楓

一応わかりやすいように点線で結んでるけど、実際は（有理数のとき存在しないため）連続じゃないから点線も怪しいよ。

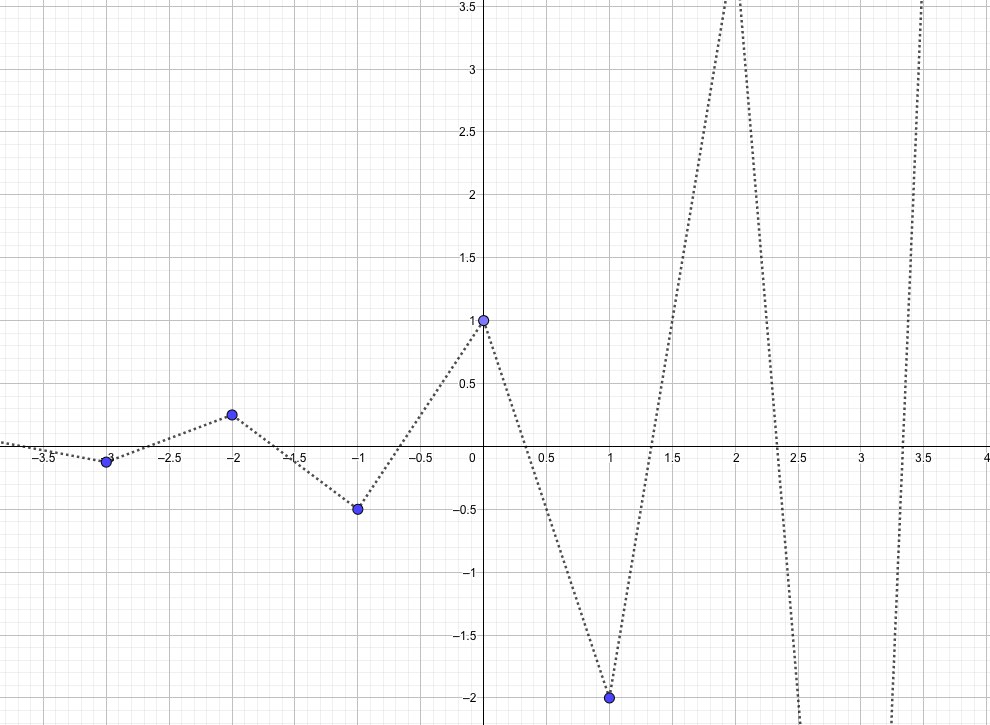
グラフを見てみるとどうでしょう。非連続だし、形は複雑だし・・・。

そもそも連続的な\(x\)を考えている座標上では、\(x\)が整数のときしかとらない非連続的な関数なんて、扱いにくくて仕方ありません。

そこで、

aが0のとき定義しない理由

ここでは、指数関数\(y=a^x\)の底\(a\)が、\(a=0\)でもOKだとしてみます。

例として、\(y=0^x\)のときを考えてみましょう。

すると、\(x=-1\)のとき\(y=0^{-1}=\frac{1}{0}\)となるため、\(x\)は整数の世界ですら考えることができなくなるのです。

小春

分母が0は数学では考えられなかったね。

つまり、\(y=0^x\)は\(x\)が正のときだけ考えることができ、グラフはこのようになります。

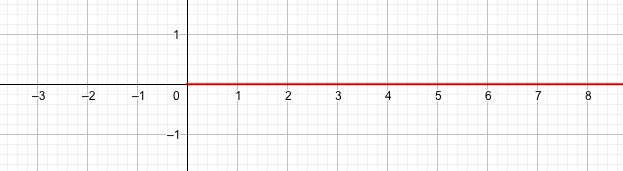
グラフから、以下の性質がわかります。

楓

・・・くそダルっ（ボソ）

口悪っ！？

小春

楓

まぁ、そのくらいめんどくさいので、定義から外そうって話よ。

また\(a\neq0\)とすることで、『指数関数は曲線だね』とまとめることもできるので、何かと都合がよろしいのです。

aが1のとき定義しない理由

ここでは、指数関数\(y=a^x\)の底\(a\)が、\(a=1\)でもOKだとしてみます。

例として、\(y=1^x\)のときを考えてみましょう。

すると、どんな実数\(x\)を当てはめても、対応する\(y\)の値が存在しますね。

小春

\(x=-1\)のとき、\(y=1\)だし、\(x=0\)のとき、\(y=1\)だし・・・。

しかも\(x=\frac{1}{2}\)のとき、\(y=1\)だね。

楓

以上のことから、\(y=a^x\)は\(x\)いつでも考えることができ、グラフはこのようになります。

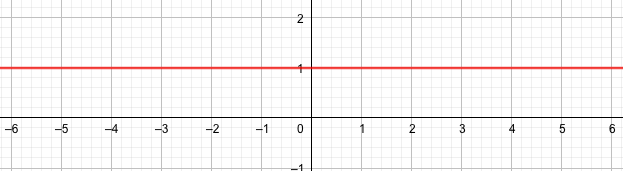
ずーーーーっと、1。

しかも直線です。

これを指数関数としてみなしても、あまり価値がありません。

楓

これを無理やり指数関数として考えることもできるけど、「指数関数は曲線だ！」って統一して言える方がよっぽど価値あるんだよね。

以上、これまでみてきたように指数関数が\(0<x<1,1<x\)の場合でしか定義されていない理由は、結局

という、気持ちが込められているからなんですね。

まとめ

楓

最後にまとめをしましょう！

指数関数は今後も、ずーっと使う関数。

だからこそ、本質を重要視して理解していて欲しいです。

数Ⅲの極限では、指数関数の『値が爆発的に増える』と言う性質が大活躍する場面もあります。

ぜひ頭の片隅に入れておいてあげてください。

以上、「指数関数の定義とその性質について」でした。