Today's Topic






こんなあなたへ
「数の集合がなぜ必要なのかわからない」
「自然数とか、整数とか、有理数とか。マジ何言ってんの?!」
この記事を読むと、この意味がわかる!
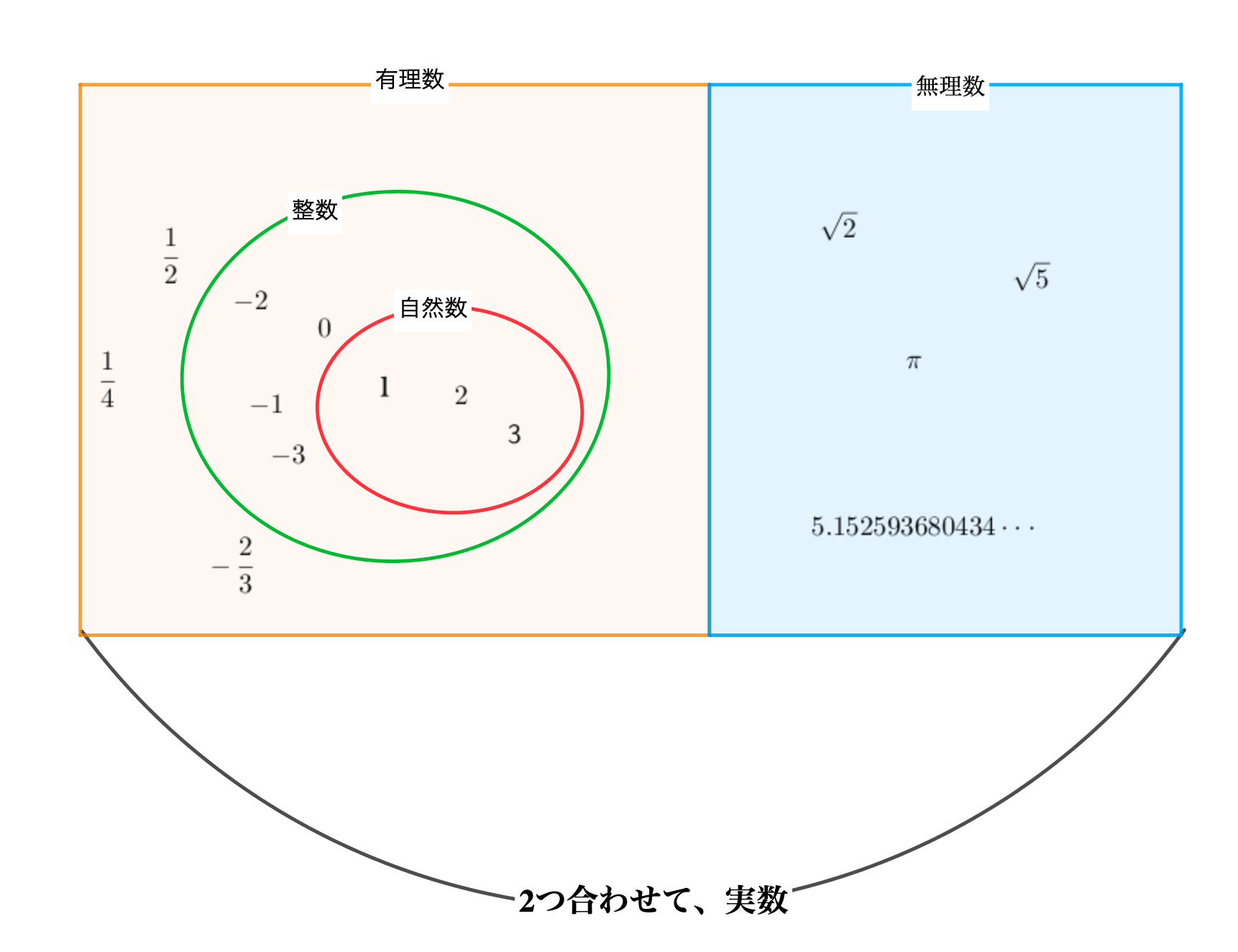
- 自然数・整数・有理数・無理数・実数の違い
- 感覚でわかる数の世界の広がり
Contents
自然数とは→モノを数えるための数
ポイント
自然数
$$1,2,3,4,\cdots$$
人は生を授かり、目を開けたとき、一番最初に何を見るのでしょうか。
笑顔で誕生を祝ってくれる人、輝く太陽、美味しそうな食べ物・・・。
ここで、
「人が何人いる」
「太陽がいくつある」
「おいしそうな食べ物が何皿ある」
など、初めて数の概念が生まれます。
この生まれたての数に共通するのは、どれも数えることができるという点。
目に見えているものが、いくつあるのか。それが最も基本的な数、自然数の特性です。
自然数の性質として押さえておきたいのは、自然数どうしの足し算と掛け算もまた、自然数になるということです。
$$1+3=4$$
$$5\times4 =20 $$
一方で、引き算、割り算になるとその答えは自然数とは限りません。
$$5-6=???$$
$$2\div 4=???$$
もちろん自然数になる時もあるのですが、足し算、掛け算の場合は、どんな自然数の組み合わせでも答えが自然数になります。


整数とは→”減る”という感覚の獲得
ポイント
整数
$$-3,-2,-1,0,1,2,3,4,\cdots$$
人間は成長していくにつれ、どんどん失うことを学んでいきます。
食べるとなくなり、大好きな人が死に、不要なモノを捨て…。
このように”減る”ということをしっかり認識するようになったことで、自然数よりも大きな整数という世界が登場しました。
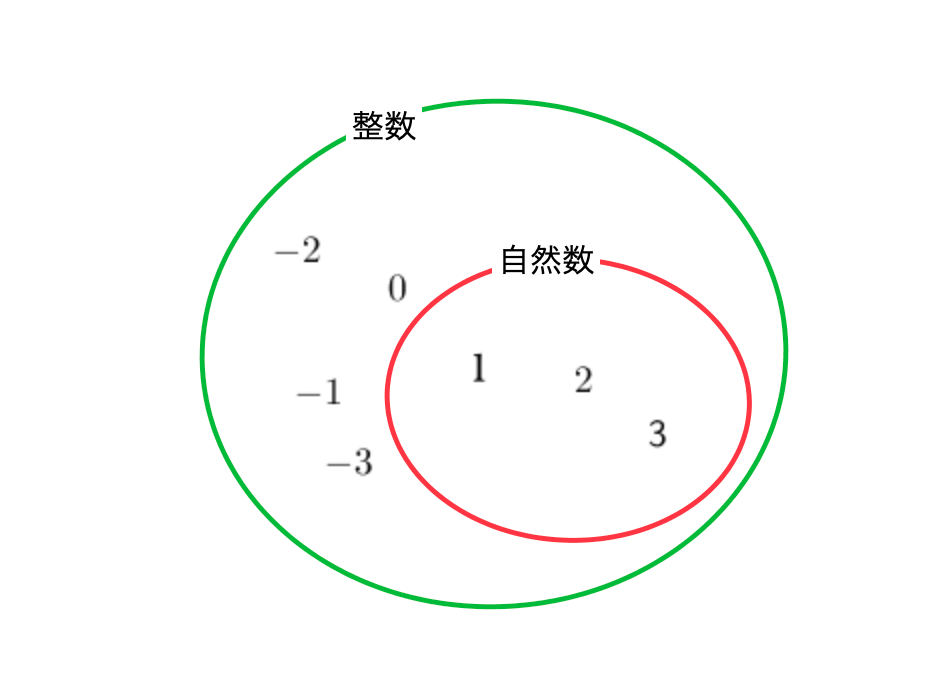

整数の性質は、整数同士の足し算、引き算、掛け算、は必ず整数になります。
$$5-6=-1$$
$$2\div 4=???$$


ちなみに大学数学までいくと、0を自然数に含めようという考え方もあります。
しかし自然数をモノを数える数として認識した時、「椅子が0個ある」なんて不自然な言葉使わないでしょ?

そもそも0という数を、数として認めるかという議論には、かなりの年月がかかっています。そういった意味でも、0は整数から登場するという認識でOKでしょう。
有理数とは→分かち合う心の獲得
ポイント
有理数
$$-1,\cdots,-\frac{1}{2},\cdots,0,\cdots,\frac{1}{2},\cdots1,\cdots$$
人間は成長するにつれて、平和や安定を求めるようになりました。
人が争う原因の一つは奪い合うこと。それを学んだ人間は”分かち合うこと”を学習します。

そこで1つのものを等しく等分する\(\frac{1}{○}\)という考え方が登場します。
これは割算のことなので、有理数になってようやく、
全ての計算が安心して行えるようになります。
$$5-6=-1$$
$$2\div 4=\frac{2}{4}$$
つまり整数までの世界で考えることができなかった、”割算を安心してできる世界”が必要になります。
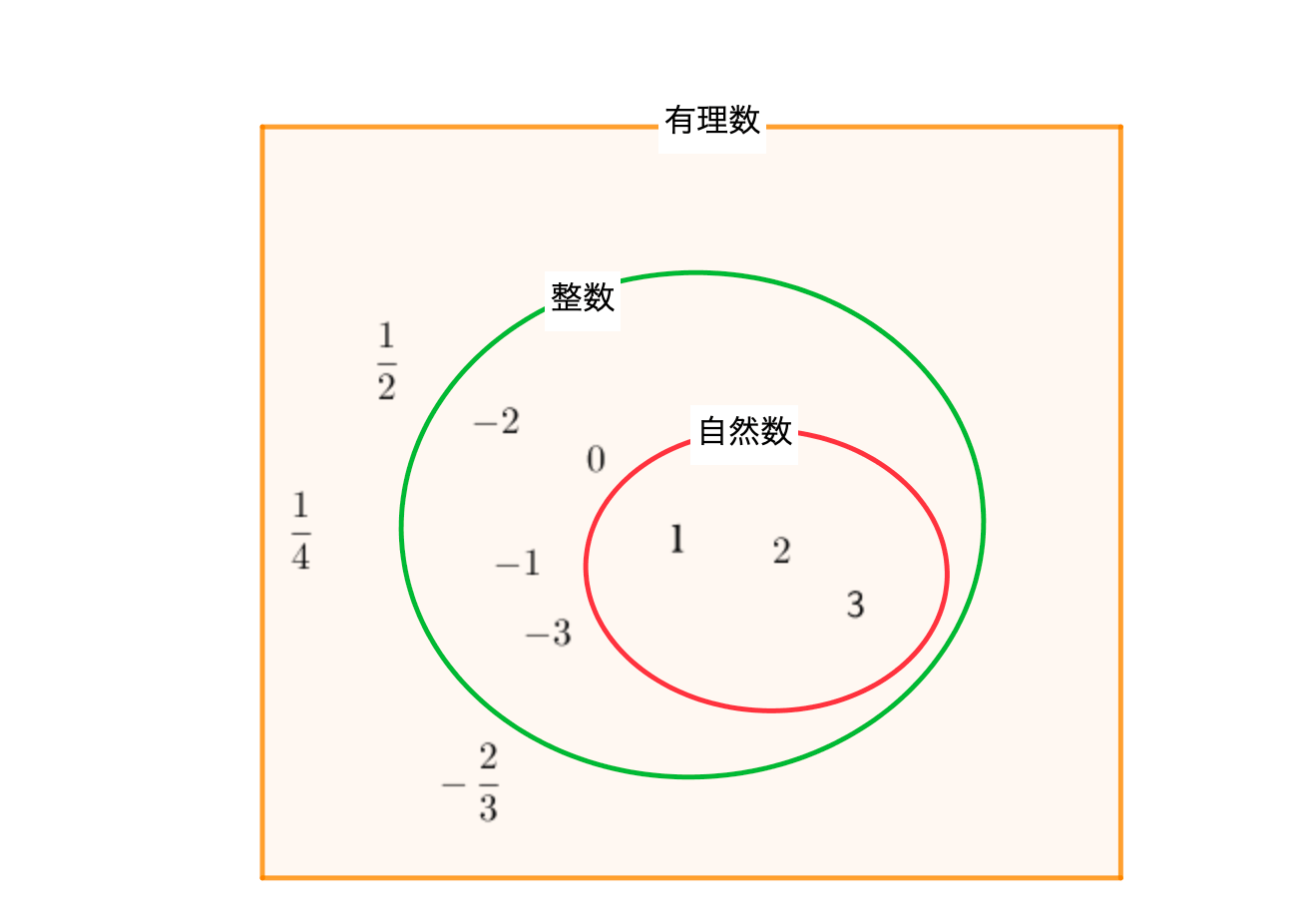
有理数の登場により、0と1の間や\(-1\)と\(-2\)の間など、並びあう整数の間に無限個の数を考えることができるようになりました。
そこで
と対応づけることにより、
よりも感覚的にわかりやすい
という小数の考え方も生まれました。
つまり
- 分数=計算のしやすさ重視
- 小数=理解しやすさ重視
という使い分けも生まれたというワケです。
このように人間は有理数で初めて、数は無限個あり、どんな2つの数を取ってもその間には無限個の数があるという"連続"の概念を手に入れました。
特性としては
- 四則計算が"基本的に"安心して行えること
- 連続的に数を捉えることができるようになったこと
が挙げられます。
無理数→”無限のヤバさ”との遭遇
有理数で初めて割り算という概念を手に入れた人間は、あるとんでもない割り算に気がつきます。
それは円という図形から発見されました。
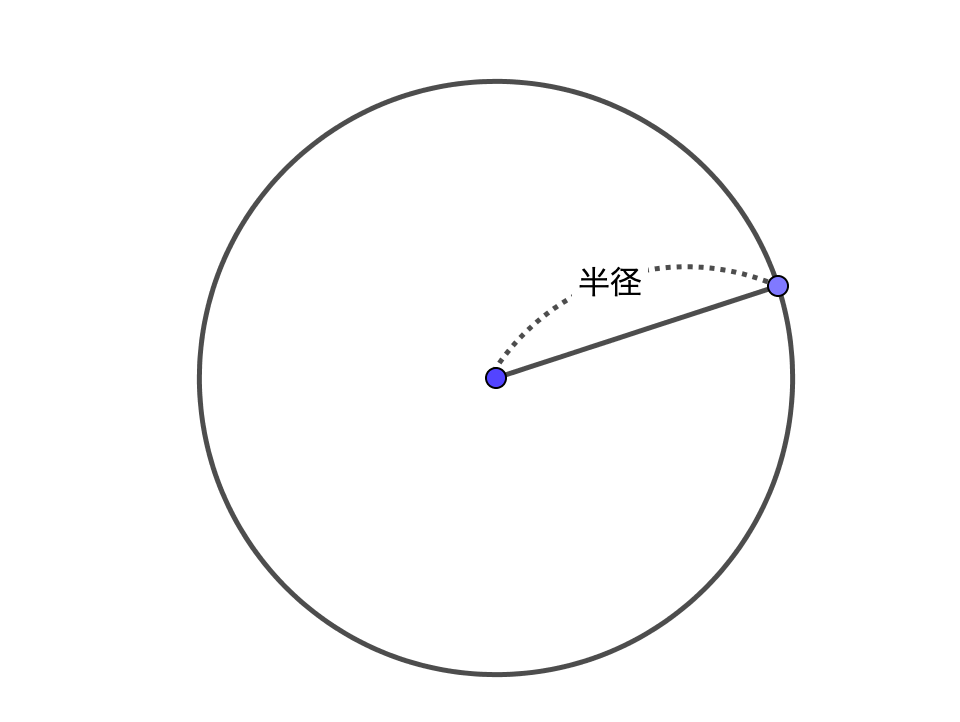
適当な半径の円を描き、その円周に糸を巻いて
を計算してみると、永遠に割り切れることのない数が登場したのです。

また背理法という証明手法を使うことにより、1辺1の正方形の対角線の長さ\(\sqrt{2}\)も割り切れないということがわかりました。
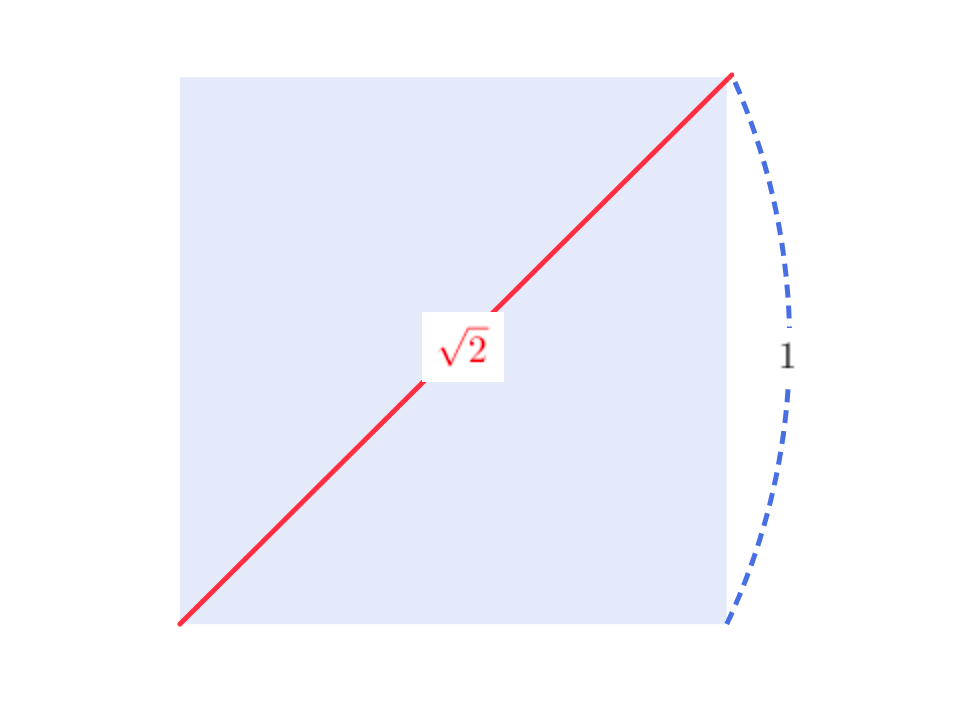
この\(\pi\)や\(\sqrt{2}\)のような数のことを無理数と呼び、有理数とは明確に区別することにしました。
無理数の特徴は分数\(\frac{1}{○}\)を計算したときに、
- 割り切れない→分数で表せない
- 小数点以下に、特に規則性のない数が羅列すること
が挙げられます。
無限に続く小数は必ず無理数か→いいえ、有理数のものもあります
有理数と無理数の段階で、よく
「無限に続く小数であれば、無理数なんだ!」
と勘違いしてしまう人がいます。
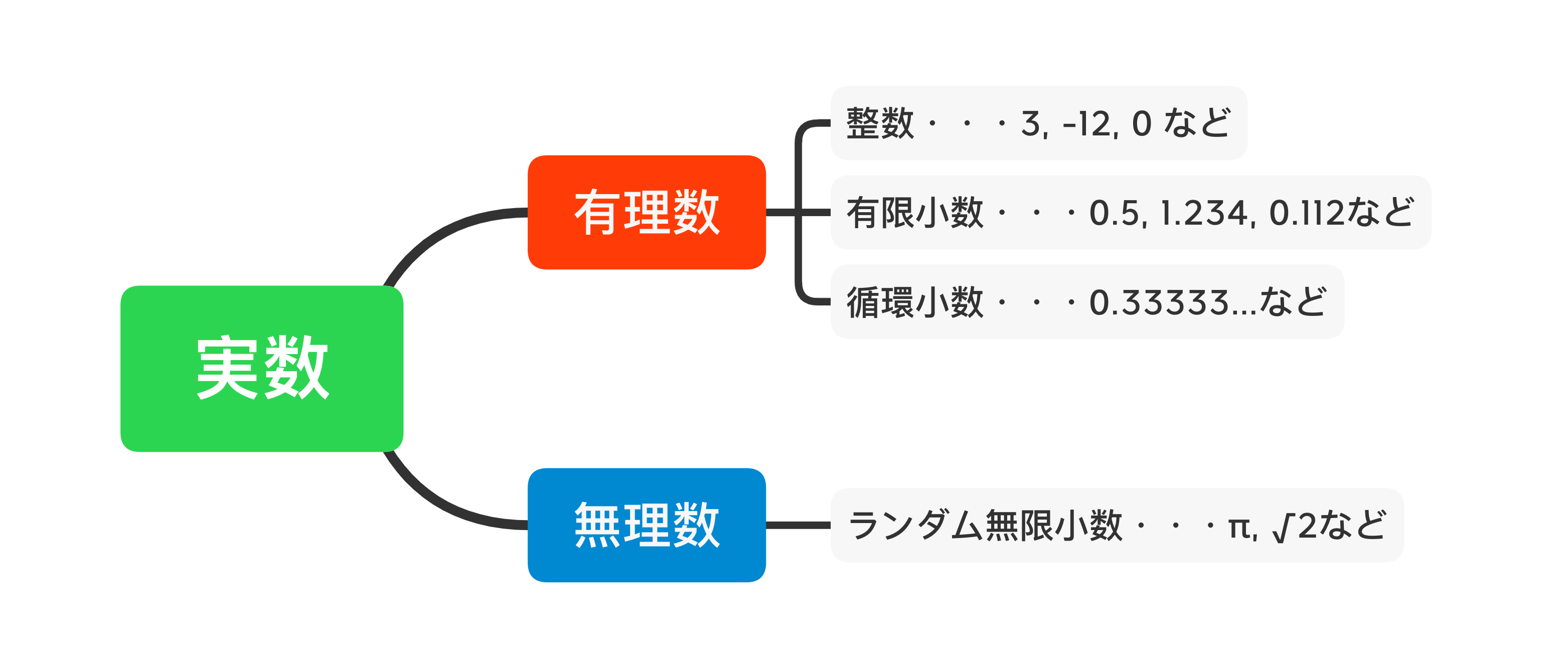
小数は以下3つに分類することができますが、この中で無理数であるものは最後の、ランダム無限小数だけです。
(例)$$0.3\ ,\ 0.6453$$
【循環無限小数】・・・同じ数やパターンが繰り返しずっと出てくる小数
(例)$$0.333333\cdots\ ,\ 0.2452452452\cdots$$
【ランダム無限小数】・・・特にパターンのない数が羅列する小数
(例)$$3.14159\cdots\ ,\ 1.4132135\cdots$$


実際に\(0.2452452452\cdots\)が有理数であることを示してみましょう。
例題
$$0.2452452452\cdots$$が有理数であることを示せ。
分数で表すことができたら有理数。
解答
とおく。両辺1000倍すると、
この2つの差をとると、
よって、
より、分数で表すことができたので有理数。

実数とは→交わらない2つの世界の総称
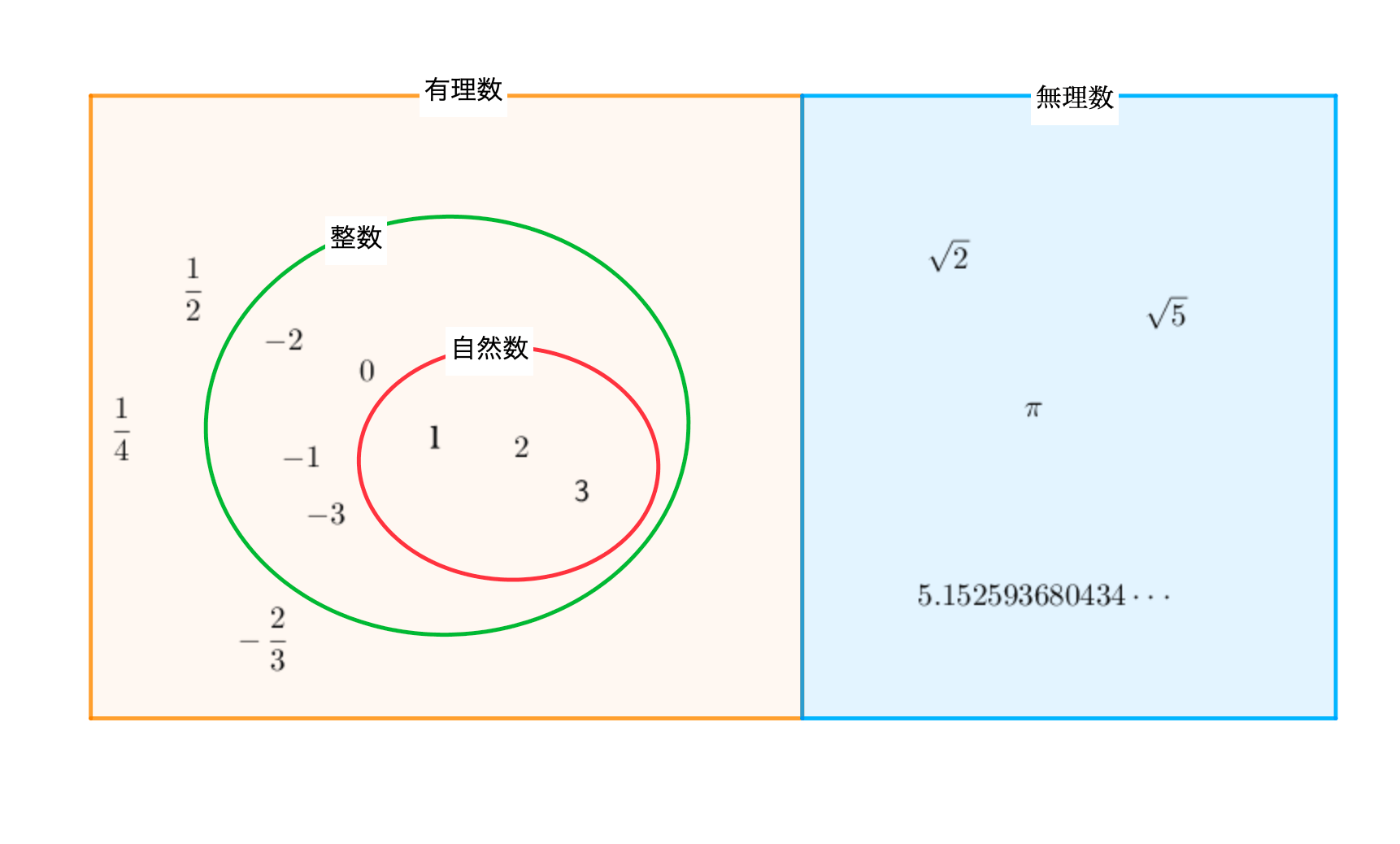
有理数は分数で表すことのできる数、一方で無理数は分数で表すことができない数です。
つまり有理数かつ無理数である数は存在しません。


有理数も無理数も、人間が成長する過程において、現実を直視して獲得した数の概念です。
そこでこの2つをまとめて実数と呼ぶことにしました。

実数はこれまでの数を全て含んでいるので、四則演算が安心してできることはもちろん、特に制限がありません。
対して、自然数や整数は引き算、割り算が安心してできるかどうかはよく検討しなければなりませんし、有理数は分数で表せるかどうかを考える必要があります。
数の世界は、小さな世界ほど考えることが多くなるのですね。
数の集合まとめ:世界が広がっていく感覚を身につけよう!


今回は数の世界の広がりを味わってもらいましたが、ちゃんと世界が広がっていく感覚を掴んでもらえたでしょうか。
数の世界それぞれの性質は、今後数学の問題を解いていく上で意外な落とし穴になりかねません。
せっかくこの記事を読んだのでしたら、今後数学の問題を解く際には
「これはどんな数の世界で言える話なんだろうか」
と少し考えてみてください。
以上、「数の世界とその特徴について」でした。








