【導関数】って結局ナニ？微分係数との違いなどを解説。

楓

よし、今日は導関数について解説するね。

導関数って、なんか微分係数と定義一緒じゃない？

小春

楓

ところが少しだけ違う。この違いがわかると、数学への理解が深まるよ！

導関数とは

関数\(f(x)\)の導関数は

で定義されます。

一般にこれは\(f'(x)\)と表されます。

また、「微分する」とは一般に、この導関数を求めることを指します。

この導関数は、関数\(f(x)\)のどこでも好きな点の\(x\)座標を代入することで、その点における微分係数、つまり接線の傾きを算出することができます。

導関数と微分係数の違い

少し出てきましたが、微分係数とは言葉の定義が若干違うので、改めて抑えておきましょう。

微分係数とは

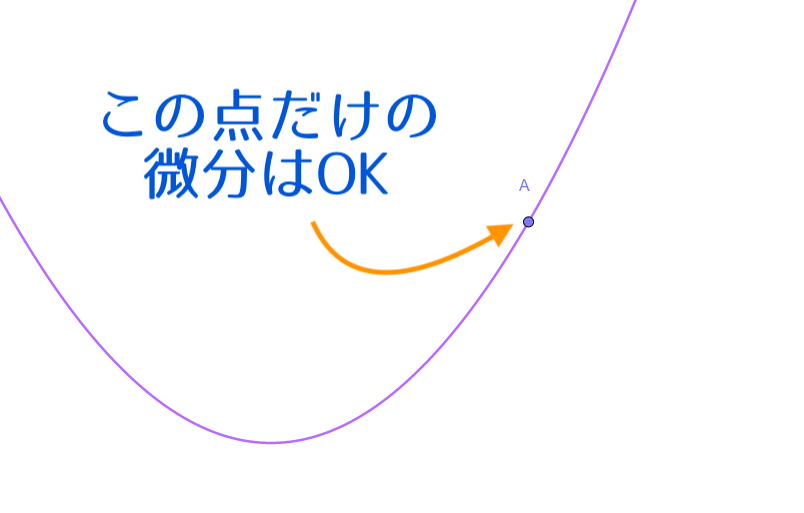
微分係数とは、関数\(f(x)\)における特定の1点の接線の傾きを表した値です。

\(f'(1)\)や\(f'(a)\ (aはある数を表す)\)など、\(x=◯\)の点のときの、接線の傾きと考えてもらえれば十分です。

導関数とは

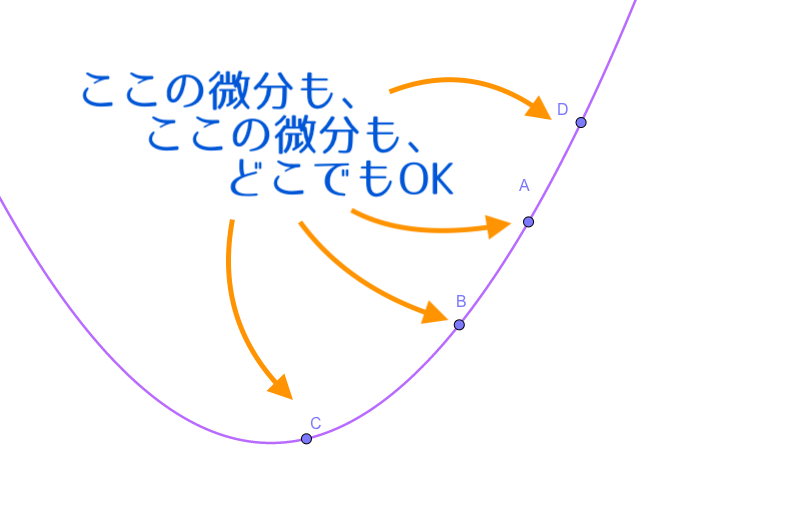
対して導関数は、関数\(f(x)\)上のどこの点の傾きでも求められる、いわゆるどこの点の微分係数でも求められる関数のこと。

\(x\)に値を突っ込むとその点における微分係数（接線の傾き）が求められます。

楓

微分係数を求めるために使う関数、という認識でOK

導関数　例題

それでは、二次関数の導関数を求めてみましょう。

早速定義に当てはめてみます。

小春

最後は\(h\to 0 \)だから、\(2x\)はそのまま残るんだね。

このように、\(h\)がうまく消えてくれるといいわけだね。

楓

導関数を効率的に求めることが攻略への近道

では3次関数はどうでしょうか。4次関数は？

ちょっとめんどくさいので、\(n\)次関数の導関数を考えてみましょう！

小春

あれ？！これ\(h\)消せる？！

一応消せるんだけど...ぱっと分からないね

楓

そう、導関数にはある問題があります。

それは導関数の定義が

• 分数であること
• 極限であること

から、かなり求めにくくなってしまっているのです。

毎回この定義通りに算出していたら、いくらチートツールでもやる気が出ません。

そこで先人たちは、関数の種類に応じて、また極限の性質を生かしていくつかの公式を編み出してくれました。

例えば、先ほどの\(n\)次関数の導関数は

という公式が約束されています。

基本的に、このような公式を用いて導関数をこれから求めることになりますが、あくまでも効率化のための公式。

丸暗記して満足しないように注意です。

楓

特に導関数の定義や意味、導出方法はしっかり押さえとかないと、導関数がいくらも求められても使い物にならないよ。

まとめ

楓

最後にまとめるよ！

ここまで理解できたなら大丈夫！

ここからは公式を紹介していきますので、意味を忘れないよう注意して勉強していきましょう！

以上、「導関数ってナニ？」でした。