Today's Topic
極大値・極小値の定義と導出の仕方




この記事を読むと、この意味がわかる!
- 極大値・極小値の意味
- 極値の存在する条件
極大値・極小値とは
| \(x\) | \(\cdots\) | \(a\) | \(\cdots\) | \(b\) | \(\cdots\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | \(\nearrow\) | \(f(a)\) 極大値 |
\(\searrow\) | \(f(b)\) 極小値 |
\(\nearrow\) |
上の増減表のように、
- \(f’(a) = 0\)
- \(x = a\)の前後で微分係数の符号が\(+ \to -\)に入れ替わっている
を満たすような\(x=a\)を考えた時、\(f(a)\)のことを極大値といいます。
また、
- \(f’(b) = 0\)
- \(x = b\)の前後で微分係数の符号が\(- \to +\)に入れ替わっている
を満たすような\(x=b\)を考えた時、\(f’(b)\)のことを極小値といいます。
グラフで考えると、図のような位置が極大値・極小値でとなっています。
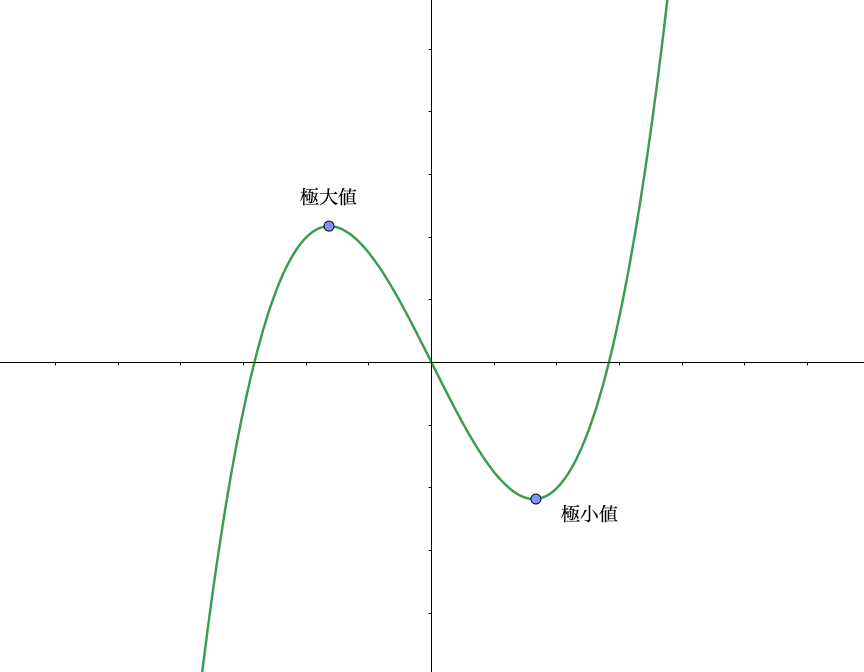


また極大値・極小値をまとめて極値ということがあります。
最大値・最小値との違い
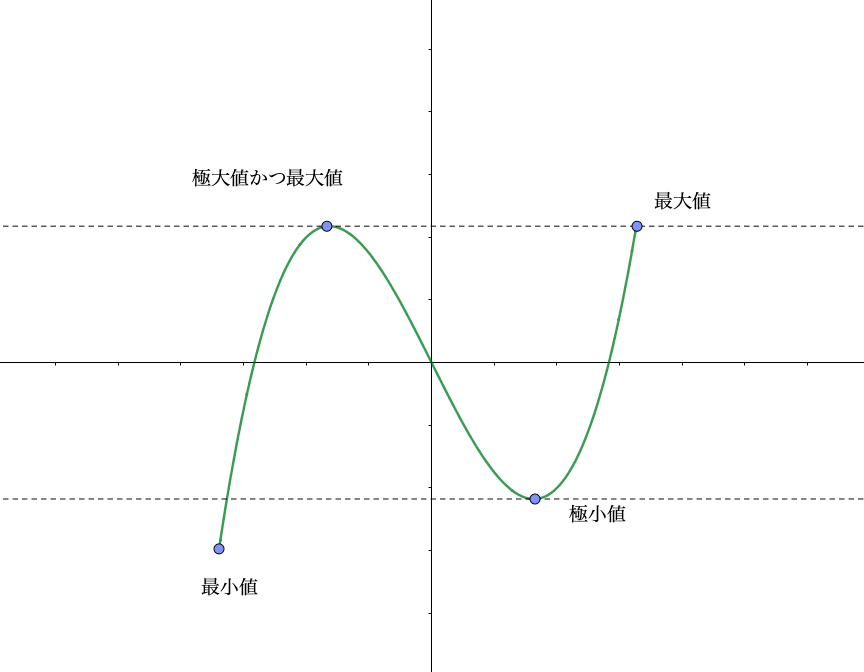
先程のグラフを見て考えると、最大値・最小値との違いに迷うかもしれません。
実は先ほど紹介した極大・極小の定義は、厳密なものではありません。
大学で扱われる極値の厳密な定義を、簡単にいうと
です。
一方で最大値・最小値の定義は
となっています。
よって極大値・極小値の判別は先ほどの2つの条件で行い、最大値・最小値の判別は定義域内の値を参考にして求めた方が良いです。
ちなみに、極大(小)値と最大(小)値が一致することもありますが、基本的には一致しないと考えたほうが良きです。
極値が存在しない場合がある
「\(x=a\)で極値(極大値&極小値)である」という条件は次の2つでした。
- \(f’(a) = 0\)
- \(x = a\)の前後で微分係数の符号が入れ替わっている
そこで、次のような例題を考えてみましょう。
例題
$$y = x^3 -1\ (-\frac{1}{2} ≦ x ≦ \frac{1}{2})$$
この三次関数の増減表とグラフは以下の通りです。
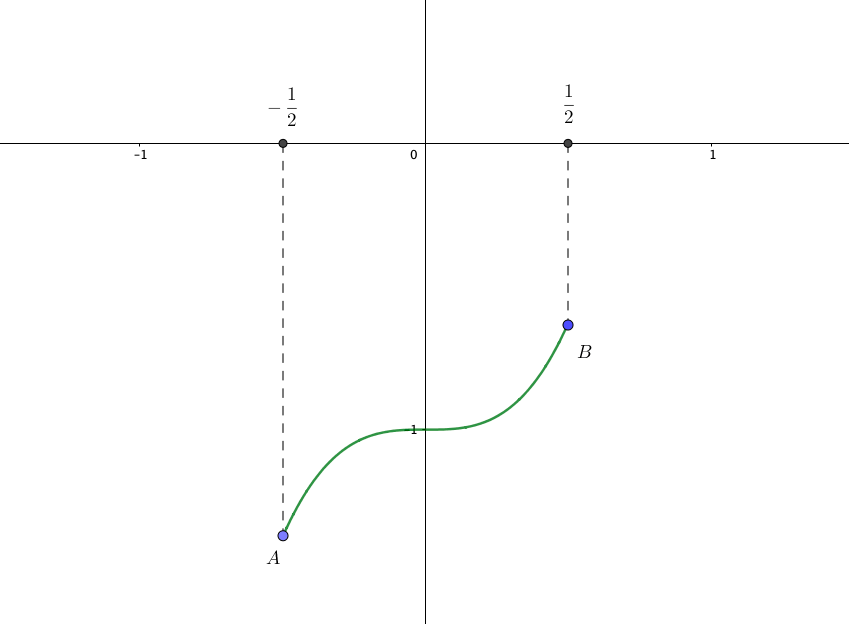
今回の増減表をみてわかるように、\(f’(a) = 0\)を満たしても、その前後で符号が入れ替わっていない場合があります。
これは2つの条件のうち1つに当てはまっていないので、この場合極値は存在しません。
しかし定義域内で最大値・最小値は存在し
- 最大値:\(x=\frac{1}{2}\)のとき、\(y = -\frac{7}{8}\)
- 最小値:\(x = -\frac{1}{2}\)のとき、\(y = -\frac{9}{8}\)
となります。
単調増加と単調減少
ちなみに先程の例題のように、常に\(f’(a) ≧ 0 \)が成り立つ場合、そのグラフは減少することなく、永遠に値が増加し続けることを意味します。
これを単調増加と言います。
反対に、常に\(f’(a)≦0\)が成り立つ場合、そのグラフは増加することなく、永遠に値が減少し続けることを意味しています。
これを単調減少と言います。
この単調増加・単調減少という条件は、グラフを考える上でかなり重要な条件になりますので、別の記事で扱いたいと思います。
まとめ

まとめ
- \(f’(a) = 0\)
- \(x = a\)の前後で微分係数の符号が\( + \to -\)に入れ替わっている
場合、\(f(a)\)のことを極大値という。
微分係数の符号が\( - \to +\)に入れ替わっている場合は極小値という。
極大値・極小値はまとめて極値と言い、極値は必ず存在するとは限らない。
文系数学において、微分の単元はかなり限定的な内容しか扱えないため、出題できる問題が少なく、極値はかなり頻出の問題です。
数Ⅲ以降では、極値の他に変曲点と呼ばれる重要な考え方が出てくるので、今のうちにしっかりと押さえておきましょう。
以上、「極大値・極小値について」でした。








