Today's Topic
関数\(f(x)\)が閉区間\([a, b]\)で連続かつ、\(f(a) \neq f(b)\)であるならば、\(f(a) < k < f(b)\)となる任意の\(k\)に対して
$$f(c) = k$$
を満たす\(c\)が\(a\)と\(b\)の間に少なくとも1つ存在する。




この記事を読むと、この意味がわかる!
\(f(x) = e^{-x-1}\)について、
$$x=f(x)$$
は少なくとも1つの解を持つことを証明せよ。ただし\(f(x)\)は連続であることは認めて良い。
中間値の定理が言いたいこと
中間値の定理が言いたいことは至ってシンプル。
まずは難しい言葉を、1つずつ消化していってみましょう。
まず前提である
という部分で、図のような\(f(x)\)のグラフが意識されています。
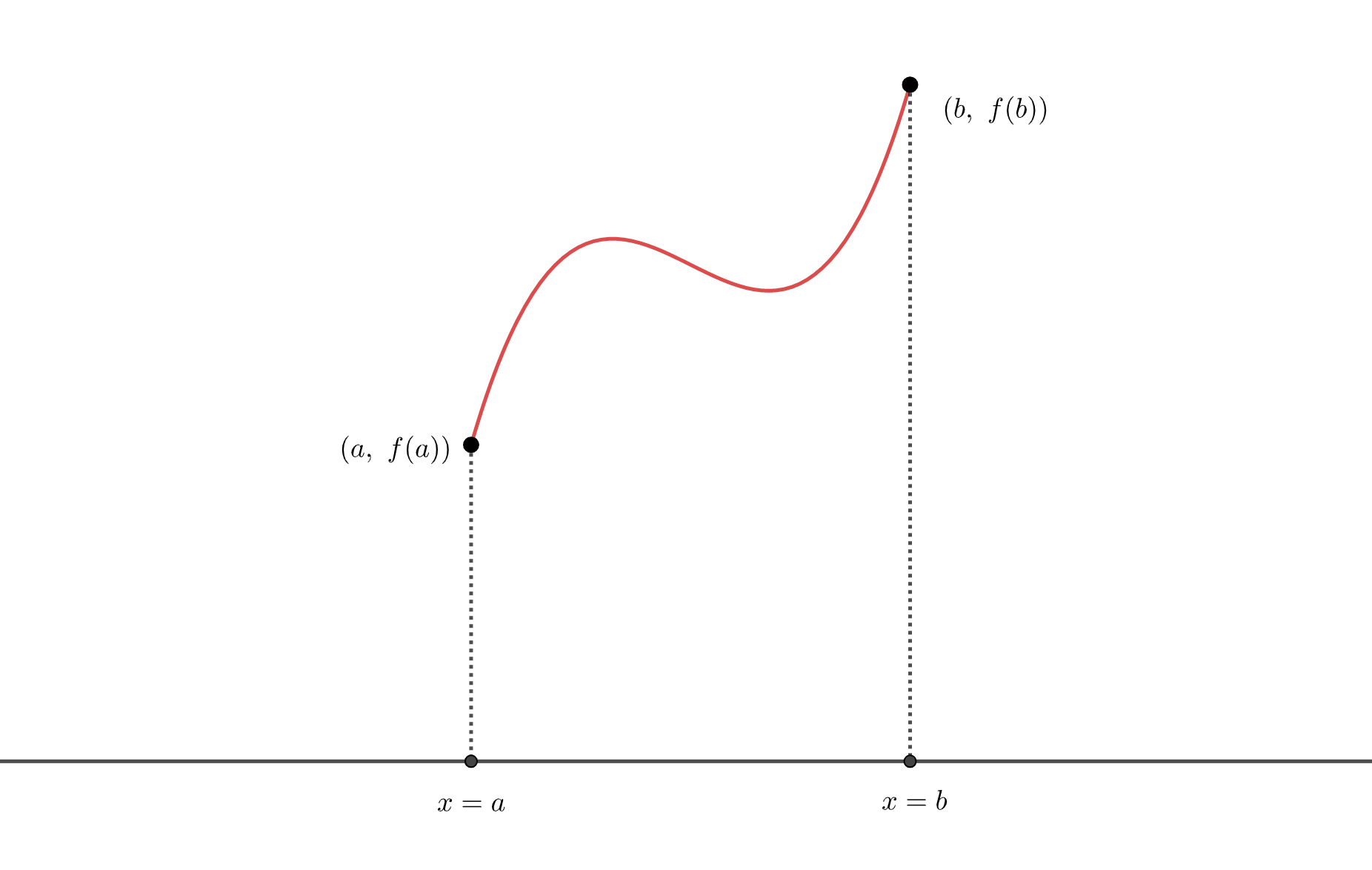


この条件のもと、
$$f(c) = k$$
を満たす\(c\)が\(a\)と\(b\)の間に少なくとも1つ存在する。
を考えてみます。
\(y\)座標が\(f(a)\)よりも高く、\(f(b)\)よりも低い適当な位置に点をとってみます。
このとき、適当にとった点の\(x\)座標はどこでも大丈夫です。
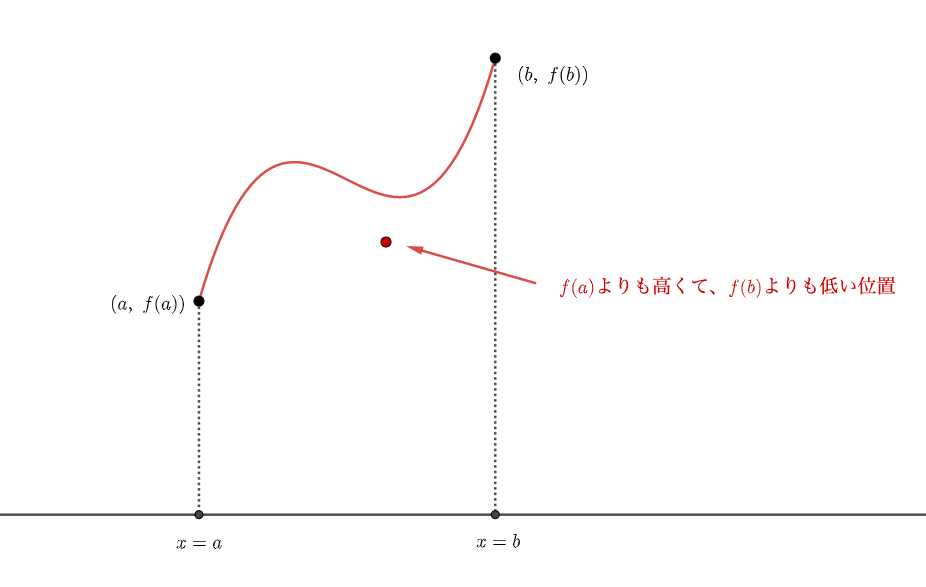
このとき閉区間\([a, b]\)の間で、適当な点と同じ高さにある点を\(f(x)\)上に見つけることができますね。
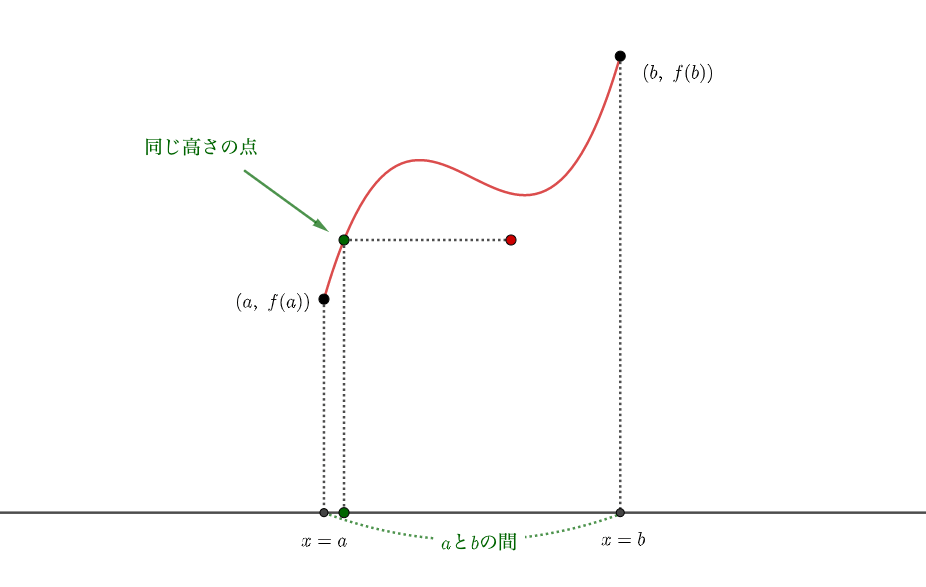
適当な高さ\(y=k\)を\(f(a)\)と\(f(b)\)の間に設定すると、閉区間\([a, b]\)の間で\(f(x)=k\)となるような\(x\)座標を必ず見つけられるよ〜

中間値の定理の使い方

例題
方程式\(2^x + x -4 = 0\)は\(1<x<2\)の範囲に、少なくとも1つの実数解を持つことを示せ。

与えられた方程式を
と考えると、\(f(x)\)は閉区間]\([1, 2]\)の間で連続的です。

閉区間上の端点\(x=1\)と\(x=2\)のときを考えてみましょう。
$$f(2) = 4 + 2 - 4 = 2$$
と、両端が異なる値となりました。
また、その\(-1\)と\(2\)の間に、与えられた方程式の右辺\(0\)が存在しますね?

以上より、
- 閉区間]\([1, 2]\)の間で連続
- \(f(1) \neq f(2)\)なので両端が異なる値である
- \(f(1) < 0 < f(2) \)
の3つの点から、中間値の定理より、
を満たす\(c\)が閉区間]\([1, 2]\)の間に必ず1つは存在することが約束されました。


【これだけは覚えて!】中間値の定理の超便利な使い方
実は中間値の定理は、
となるような\(x\)の値が、特定の閉区間で存在することを示すのにむちゃくちゃ便利です。
例を見てみましょう。
例題
次の方程式
$$f(x) = 2^x + 4^{\frac{3}{x}} -5x=0$$
は閉区間\([2,4]\)の間に解を持つか。
ご覧の通り、むちゃくちゃめんどくさい方程式が出てきたとします。
これを解く以前に、そもそもこいつは解を持つのかどうかがわかれば、解答の指針を立てやすくなりますね?
さて、本当は連続であることの証明から入りたいですが、高校数学では基本的に連続関数しか扱わないので、ここでも連続であることを前提に扱いましょう。
閉区間の端点\(x=2\)と\(x=4\)をそれぞれ代入すると、
$$f(4) = 2^{4}+4^{\frac{3}{4}} -20 < 0$$
であることがわかりますね。


2つの端点は異符号なので、その間に必ず0を挟む事になります。
つまり\(f(2) < 0 < f(4)\)であることは確定したので、中間値の定理より、
を満たすような\(x\)の値が1つはあることが約束されるというわけです。
\(f(x)\)が与えられた閉区間上で、連続かつ端点の符号が異なるならば、必ず\(f(x) = 0\)を満たす\(x\)の値が存在することが中間値の定理からわかる!
まとめ

まとめ
\(f(x) = k\)の解\(x\)が最低1つは存在することを確かめるためには、
- 与えられた方程式\(f(x)\)が閉区間上で連続であること
- 閉区間\([a,b]\)の端点の値\(f(a),\ f(b)\)が異なること
- \(f(a) < k f(b)\)であること
を示し、中間値の定理を用いれば良い。
特に、\(f(x) = 0\)の解が少なくとも1つ存在することを示したい(確認したい)場合、
- 与えられた方程式\(f(x)\)が閉区間上で連続であること
- 閉区間\([a,b]\)の端点の値\(f(a),\ f(b)\)が異符号であること
だけを示せれば良い。



どうでしょう、少しでもイメージ掴めましたか?
下の練習問題もぜひ一度やってみてください!
以上、「中間値の定理の意味と使い方について」でした。
チェック問題
例題
\(f(x) = e^{-x-1}\)について、
$$x=f(x)$$
は少なくとも1つの解を持つことを証明せよ。ただし\(f(x)\)は連続であることは認めて良い。
2013年日大/医4 改
\(g(x) = f(x) - x = e^{-x-1} -x\)とする。
連続関数同士の差もまた連続関数となるので、\(g(x)\)は任意の区間で連続である。
ここで勘で適当な閉区間\([2,4]\)を考えてみましょう。
$$g(4) = e^{-5} -5 < 0$$


では幅を広げて閉区間\([-1,4]\)のときはどうでしょうか?
$$g(4) = e^{-5} -5 < 0$$

以上より、
- \(g(x) = f(x) - x \)は任意の区間で連続である
- 閉区間\([-1,4]\)のとき、2つの端点は符号が異なる
ことから、中間値の定理より、\(g(x) = 0\)を満たす解\(x\)は閉区間\([-1,4]\)の間に少なくとも1つはある。
よって\(x=f(x)\)は、閉区間\([-1,4]\)の間に少なくとも1つの解を持つ。








