【微分の計算法則】和・差・定数倍・定数・xのn乗の計算方法と証明

Today's Topic

$$\left(x^n\right)'=nx^{n-1}$$

$$\left\{k\,f(x)\right\}'= k\,f'(x)(kは定数)$$

$$\left\{f(x)\pm g(x)\right\}'= f'(x)\pm g'(x)$$

$$k ' = 0\ (kは定数)$$

（※見切れている場合はスクロール）

楓

ここでは微分の基本的な計算法則を見ていくよ。

これをマスターするとどうなるの？

小春

楓

そうだね、微分公式をさらに簡単にすることができるかな！

なるほど、避けては通れない道ってことね・・・。

小春

この記事を読むと、この意味がわかる！

関数$f(x)=x^3-2x^2+1$を微分せよ。
関数$\frac{1}{3}x^3-2x^2+x$を微分せよ。

楓

答えは最後にあるよ。

Contents

1 $x^n$の微分
2 定数倍された関数$kf(x)$の微分
3 ２つの関数の和$f(x)+ g(x)$の微分
4 ２つの関数の差$f(x)- g(x)$の微分
5 定数の微分
6 まとめ

$x^n$の微分

最初に$x^n$の導関数を紹介しておきましょう。

この公式はとっても覚えやすい形をしています。

ポイント

$$\left(x^n\right)'=nx^{n-1}$$

イメージとしては、肩の荷を前に下ろして、1軽くするという感じ。

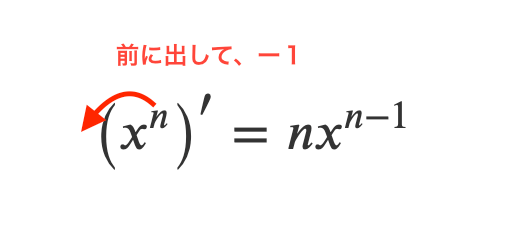
ただし、この公式の証明は少しハードルが高いです。

文系の方であれば、コツさえ掴めば指数$n$が自然数であれば証明できるでしょう。

しかしどんな数のときでも、この公式が成り立つという証明には、数Ⅲの知識をかなり取り入れる必要があるのです・・・。

この証明は少し長くなるので、別記事で取り扱いますね。

: 【べき乗の微分公式】x^nの微分は実は難しい。知ってれば差がつく公式証明

続きを見る

楓

数ⅡBと書いてあるところは、文系さんでもマスターできますよ！

例題

$f(x)=\frac{2}{3}x^6$とする。$f'(x)$を求めよ。

（解答）\begin{align} f'(x) &=\left(\frac{2}{3}x^6\right)' \\\ &= 6\cdot \frac{2}{3} x^{(6-1)}\\\ &=4x^5\\\ \end{align}

定数倍された関数$kf(x)$の微分

$k$を定数としたとき、次のことが成り立ちます。

定数倍された関数の微分

$$\left\{kf(x)\right\}'= kf'(x)$$

これは導関数の定義から、ほとんどそのまま求められるので大して難しくありません。

\begin{align} \left\{k\,f(x)\right\}' &= \lim_{h\rightarrow 0}\frac{k\,f\left(x+h\right)-k\,f\left(x\right)}{h}\\\ &= \lim_{h\rightarrow 0}k\left(\frac{f\left(x+h\right)-f\left(x\right)}{h}\right)\\\ &= k\cdot\lim_{h\rightarrow 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}\\\ &= k\,f'(x)\\\ \end{align}

（※見切れている場合はスクロール）

つまり関数が何倍されようとも、微分すれば直接影響しないということですね。

例題

$f(x)=2x^2+4x$を微分せよ。

（解答）\begin{align} f'(x) &= 2\left(x^2+2x\right)'\\\ &= 2\left(2x+2\right)\\\ &= 4x+4\\\ \end{align}

２つの関数の和$f(x)+ g(x)$の微分

2つの関数$f(x),g(x)$を考えます。このとき、以下のことが成り立ちます。

和の微分法

$$\left\{f(x)+g(x)\right\}'= f'(x)+g'(x)$$

小春

2つの関数の和の微分は、それぞれの関数を微分して、もう一回足せばいいのね！

この証明は、ただひたすら極限と向き合うのみ。

ポイントは、導関数の定義の形を無理やり作ってあげることです。

\begin{align} \left\{f(x)+g(x)\right\}' &= \lim_{h\rightarrow 0}\frac{\left(f\left(x+h\right)+g\left(x+h\right)\right)-\left(f\left(x\right)+g\left(x\right)\right)}{h}\\\ &= \lim_{h\rightarrow 0}\frac{f\left(x+h\right)+g\left(x+h\right)-f\left(x\right)-g\left(x\right)}{h}\\\ &= \lim_{h\rightarrow 0}\frac{\left(f\left(x+h\right)-f\left(x\right)\right)+\left(g\left(x+h\right)-g\left(x\right)\right)}{h}\\\ &= \lim_{h\rightarrow 0}\left(\frac{f\left(x+h\right)-f\left(x\right)}{h}+\frac{g\left(x+h\right)-g\left(x\right)}{h}\right)\\\ &= \lim_{h\rightarrow 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}+ \lim_{h\rightarrow 0}\frac{g\left(x+h\right)-g\left(x\right)}{h}\\\ &= f'(x)+g'(x)\\\ \end{align}

（※見切れている場合はスクロール）

例題

$f(x)=2x^2,g(x)=3x$とする。$\left\{f(x)+g(x)\right\}'$を求めよ。

（解答）\begin{align} \left\{f(x)+g(x)\right\}' &= f'(x)+g'(x)\\\ &= 4x+3\\\ \end{align}

２つの関数の差$f(x)- g(x)$の微分

2つの関数$f(x),g(x)$を考えます。このとき、以下のことが成り立ちます。

差の微分法

$$\left\{f(x)-g(x)\right\}'= f'(x)-g'(x)$$

小春

あんまり和のときと変わらないね！

こちらの証明は、和のときとほとんど変わりません。

符号を変えるだけ、ぜひ自分の手で解いてみてください。

定数の微分

定数$k$を変数$x$について微分、つまり導関数を求めるとどうなるのでしょうか。

結論から言うと、次のようになります。

定数の微分

$f(x)=k$のとき、

$$f'(x) = 0$$

小春

え、定数は微分すると0になるの？

実際に証明してみましょう。

大丈夫、これも導関数の定義に従うだけです。

\begin{align} f'(x) &= \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\\\ \end{align}

$f(x)=k$は変数$x$を含んでいないため、$x$の値に依存せず、ずっと定数$k$のままです。

つまり

$$f(x+h) - f(x) = k - k = 0$$

となるので、

\begin{align} f'(x) &= \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\\\ &= \lim_{h\to 0} \frac{0}{h}\\\ &= \lim_{h\to 0 } 0\\\ &= 0\\\ \end{align}

となります。

例題

$f(x)=2x^2+11$とする。$f'(x)$を求めよ。

（解答）\begin{align} f'(x) &= \left(2x^2+11\right)'\\\ &= (2x^2)'+(11)'\\\ &= 4x^2 + 0\\\ &= 0 \\\ \end{align}

小春

和の形の微分公式のおかげで分解して考えることができるんだね。

まとめ

お疲れ様でした。

今回ご紹介した覚えるべき微分法の公式は以下の４つ。

まとめ

$$\left(x^n\right)'=nx^{n-1}$$

$$\left\{k\,f(x)\right\}'= k\,f'(x)(kは定数)$$

$$\left\{f(x)\pm g(x)\right\}'= f'(x)\pm g'(x)$$

$$k' = 0$$

（※見切れている場合はスクロール）

どれも微分の計算には欠かせない公式なので、早めに覚えてしまいましょう。

以上、「微分の計算法則について」でした。

チェック問題

例題

関数$f(x)=x^3-2x^2+1$を微分せよ。

（解答）$$f'(x)=3x^2-4x$$

例題

関数$\frac{1}{3}x^3-2x^2+x$を微分せよ。

（解答）$$x^2-4x+1$$

【微分の計算法則】和・差・定数倍・定数・xのn乗の計算方法と証明

\(x^n\)の微分

【べき乗の微分公式】x^nの微分は実は難しい。知ってれば差がつく公式証明

定数倍された関数\(kf(x)\)の微分

２つの関数の和\(f(x)+ g(x)\)の微分

２つの関数の差\(f(x)- g(x)\)の微分

定数の微分

まとめ

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則