Today's Topic
関数\(f(x)\)が\(x=a\)において微分可能であるとは、\(x=a\)で連続かつ、$$f'(a)=\lim_{h\rightarrow 0}\frac{f\left(a+h\right)-f\left(a\right)}{h}$$が存在するときをいう。




この記事を読むと、この問題が解ける!
- 関数\(y=\frac{1}{x}\)は\(x=0\)で微分可能か
- 関数$$y=\left\{ \begin{array}{l} 0\ (x≦0) \\ x^2\ (0≦x) \end{array} \right. $$は\(x=0\)で微分可能か

Contents
微分可能であることの定義
数学では「この関数のこの部分では、微分ができるよ」というのを「微分可能」と言います。
その微分可能であることの定義は、次の通り。
微分可能の定義
関数\(f(x)\)がある区間\(I\)において微分可能であるとは、区間\(I\)上のどの点でも$$f'(x)=\lim_{h\rightarrow 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}$$が存在するときをいう。
微分可能であるためには、「連続であること」が必須条件
ただしこの定義だけ見ると、「連続である」ということの重要性を見逃しがち。
まずは微分の定義を思い出してください。
微分の定義は、
と表され、2つの点を近づけるというイメージがありました。
連続でない場合、2つの点を近づけることができず、微分を考えることはできません。


微分可能であるならば、グラフは連続であることの証明
微分可能であることの前提として、「連続である」ということが必須でした。
つまり微分可能であることが示せた場合は、その前提である「連続である」ことも示せているということですね。
問題
関数\(f(x)\)が点\(x=a\)で微分可能であるならば、連続であることを示せ。
関数\(f(x)\)が点\(x=a\)で微分可能である
(※見切れている場合はスクロール)
これは
(※見切れている場合はスクロール)
が成り立つことに他ならない。
すなわち、右極限と左極限が\(f(a)\)で一致するので、関数\(f(x)\)は\(x=a\)で連続。
ポイント
連続でも、微分可能じゃない場合がある






論理と命題を理解していればわかりますが、『微分可能であれば連続である』が成り立つからといって『連続であれば微分可能である』ということはできません。


この2つの命題の関係を逆(命題)といい、どちらも成り立つかどうかは一方ずつ確かめる必要があります。
そしてこの『連続であれば微分可能である』には反例が存在します。


問題
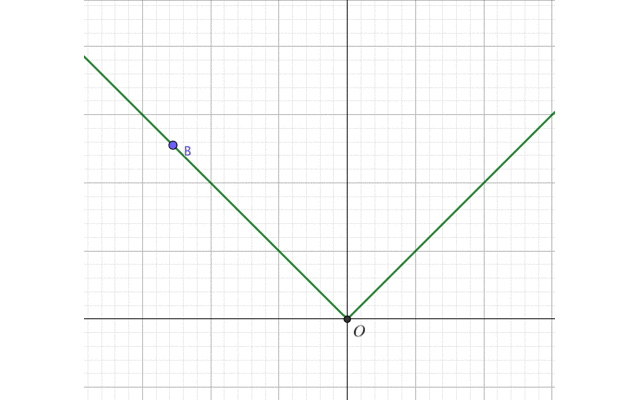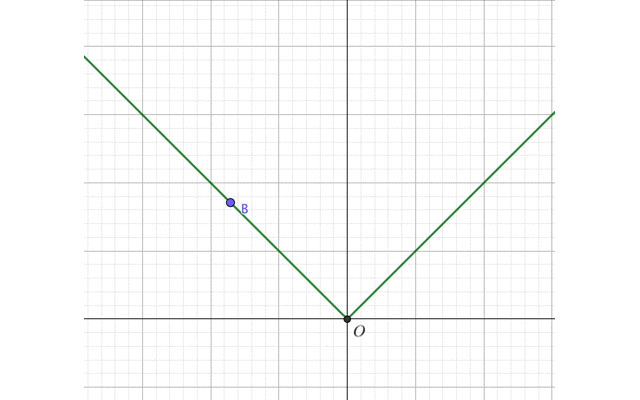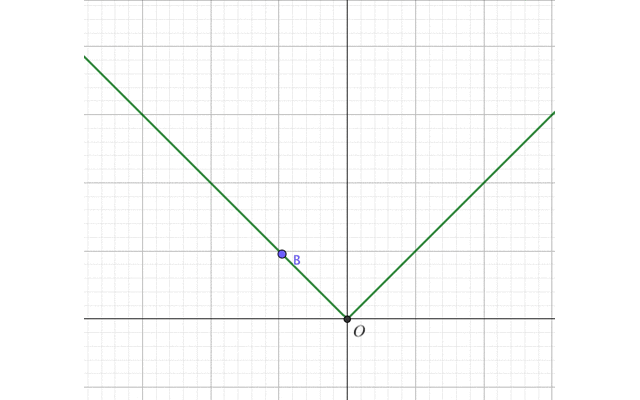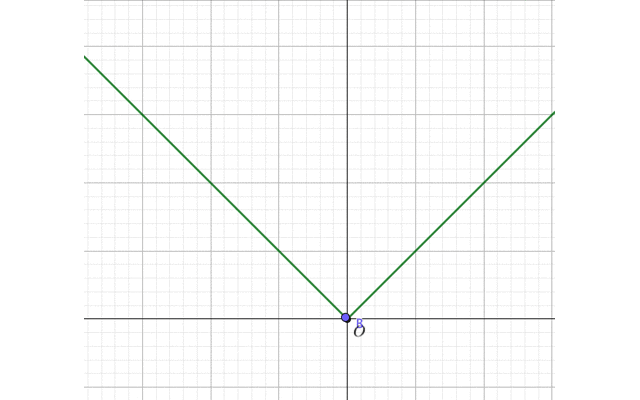
関数\(f(x)=|x|\)は\(x=0\)で微分可能か。
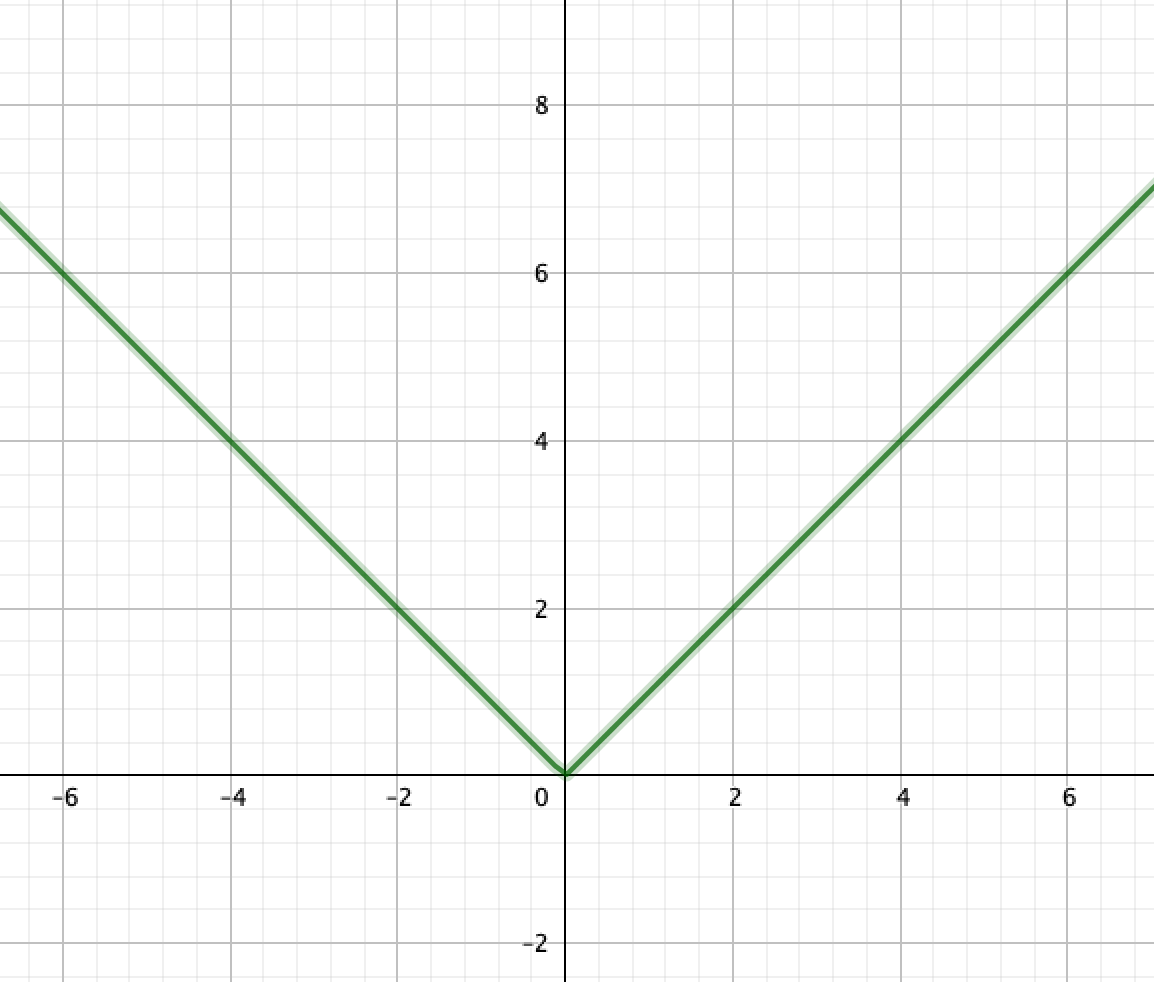



\(x=0\)において
$$\lim_{h \to -0}f(0+h)=f(0)=0$$
右極限と左極限が一致したので、\(x=0\)で関数\(f(x)=|x|\)は連続。
ところが
より
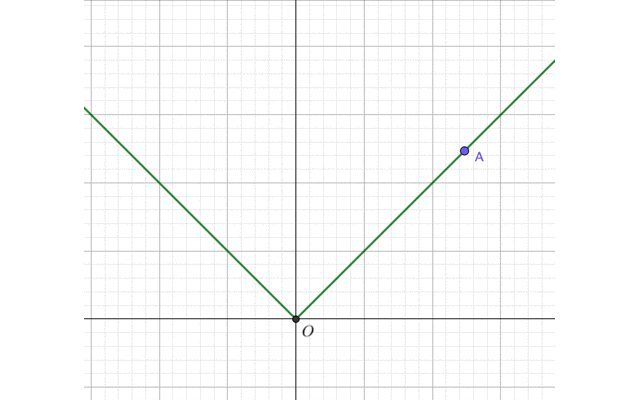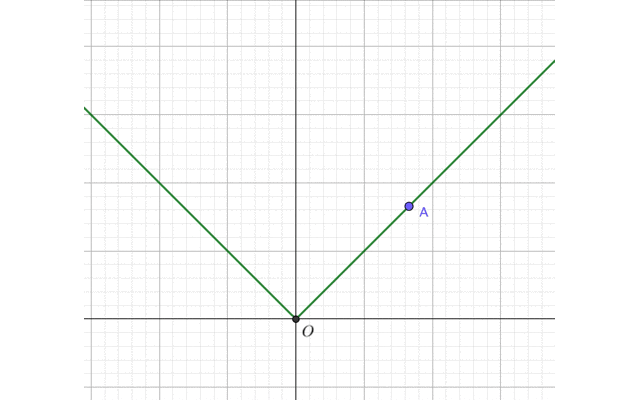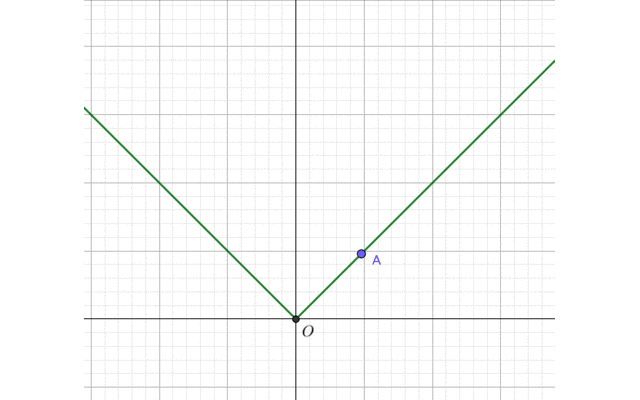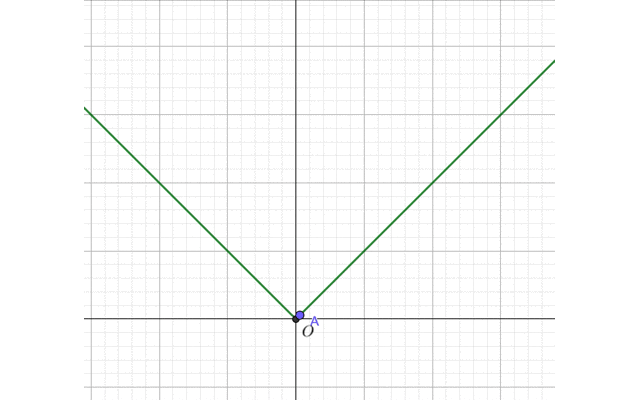


より
(※見切れている場合はスクロール)


よって
が存在しないので、微分不可能。
すなわち関数\(f(x)=|x|\)は連続であるが、微分不可能。
このように、とがっている部分では、微分することができません!


微分可能か調べるチェックテスト
ここまでの内容をまとめると、
- 微分したい点において、その関数が連続
- 微分したい点において、その関数がとがっていない
ときに微分することができました。
つまり
ポイント
微分可能かチェックするためには、
- グラフを書いて微分する点でグラフが連続かつ滑らかであるか見てみる
- グラフが微分する点において、微分可能の定義を満たすかチェックする
のどちらかを実施すればいい
というわけです。


微分可能とは?|まとめ


お疲れ様でした。
それでは今日抑えておきたいポイントをまとめます。
まとめ
- 微分可能であるならば連続である。
- 連続であっても微分可能とは限らない(反例:\(f(x)=|x|\))
- 微分可能か調べるためには、関数\(f(x)\)が\(x=a\)において
$$f'(a)=\lim_{h\rightarrow 0}\frac{f\left(a+h\right)-f\left(a\right)}{h}$$
(※見切れている場合はスクロール)
が存在することを示せばよい。 - グラフのとがっている部分では、連続でも微分することはできない。
微分可能な関数は、連続であることが前提条件。
ここは今後も重要なポイントになるので、下玉の片隅に入れておきましょう。




以上、「微分可能であるとは何か」でした。
チェック問題
例題
関数\(y=\frac{1}{x}\)は\(x=0\)で微分可能か
関数\(y=\frac{1}{x}\)は、グラフより\(x=0\)では連続ではない。
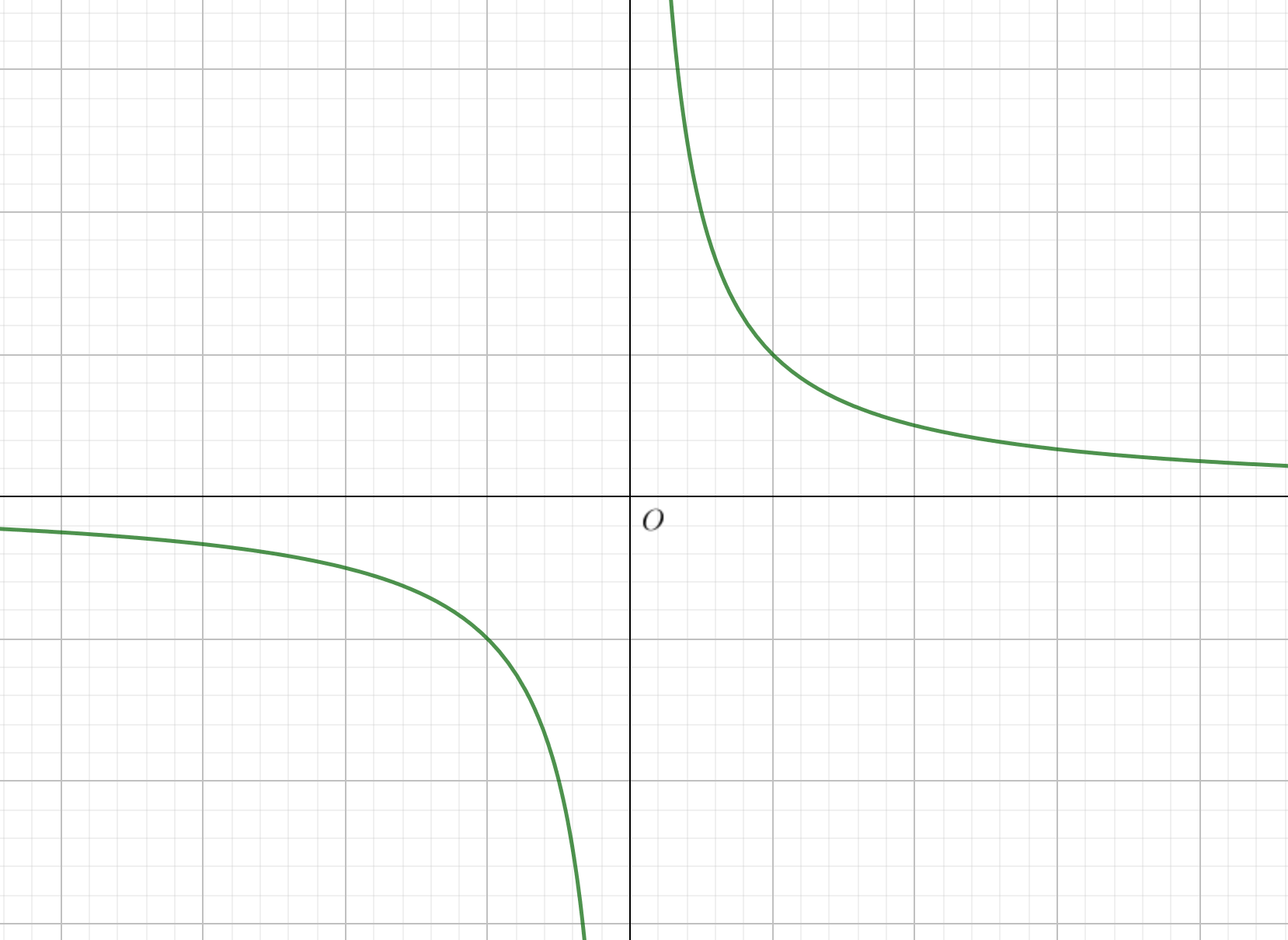

よって、\(x=0\)では微分不可能。
例題
関数$$y=\left\{ \begin{array}{l} 0\ (x≦0) \\ x^2\ (0≦x) \end{array} \right. $$は\(x=0\)で微分可能か
グラフを描いてみると、与えられた関数は\(x=0\)で連続である。
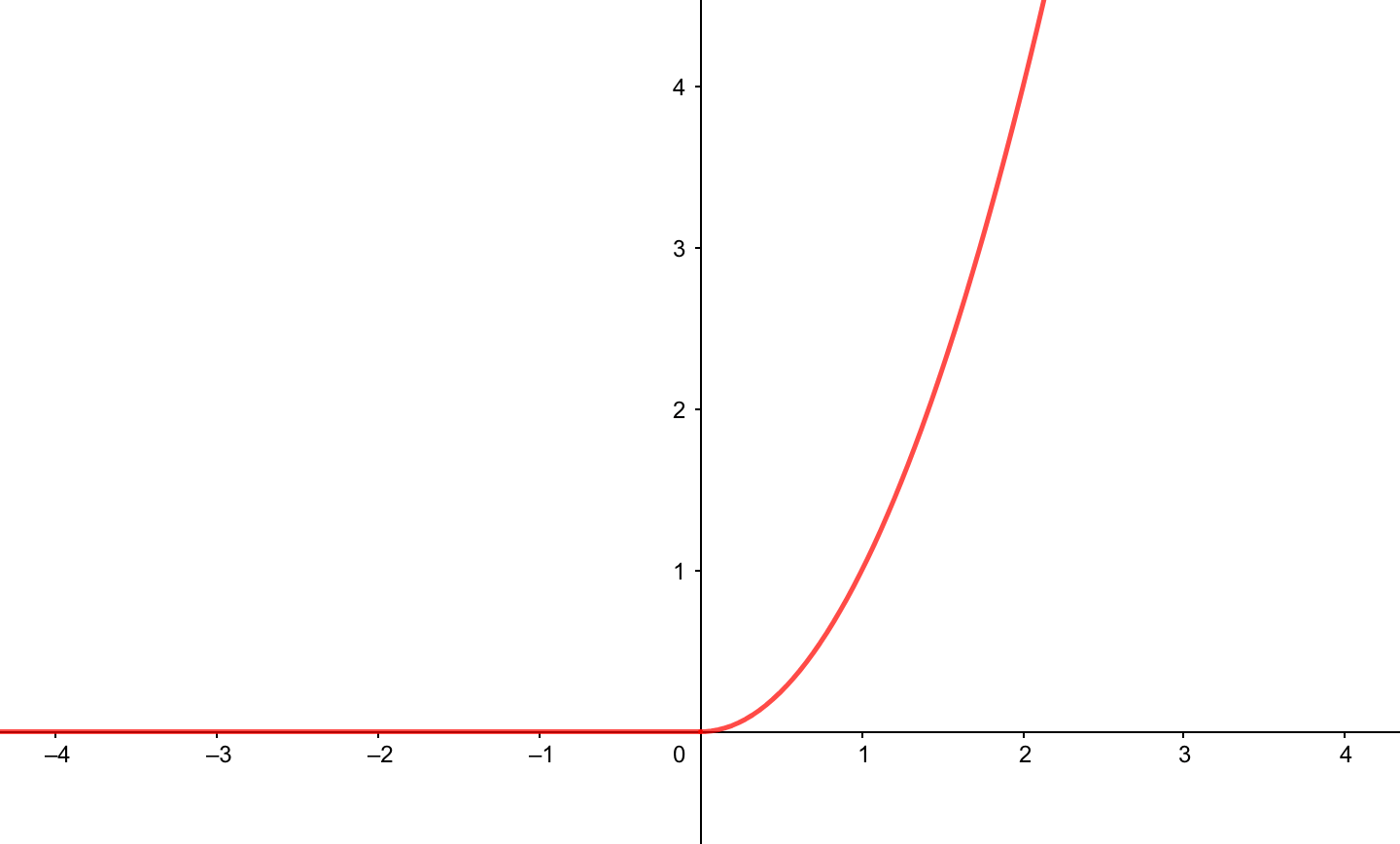

また、
$$\lim_{h\rightarrow +0}\frac{f\left(0+h\right)-f\left(0\right)}{h}=0$$
$$\lim_{h\rightarrow -0}\frac{f\left(0+h\right)-f\left(0\right)}{h}=0$$
より、$$\lim_{h\rightarrow 0}\frac{f\left(0+h\right)-f\left(0\right)}{h}=0$$が存在する。
よって、\(x=0\)で微分可能で、微分係数は0である。









