Today's Topic
- \(x\)と\(y\)が一対一のときのみ、逆関数は存在する。
- 逆関数を求めるためには、関数\(y=f(x)\)を\(x=(yの式)\)の形にし、最後に\(x\)と\(y\)を入れ替えれば良い。




この記事を読むと、この問題が解ける!
- 関数\(y=7^x\)の逆関数を求めよ。
- \(y = -x^2 + 3x +4\ (-1< x < \frac{1}{2})\)のとき、逆関数を求めよ。
Contents
逆関数講座|【準備】関数の定義

関数は中学校の頃から導入されますが、あなたは関数とは一体何か説明できますか?
「方程式と区別がつかなかったなぁ」なんていう人は、そもそも関数の意味が理解できていないことが多いです。
ここでは長くなるので割愛しますが、別記事でわかりやすく解説しているので、関数の説明ができない人は絶対に復習しておいて下さい!
参考【関数とは】中学生でも大丈夫!曖昧にしがちな関数の特徴をしっかりマスターしよう
逆関数講座|逆関数とは
ここでは具体的に考えてみましょう。
まずは一次関数\(y=3x+1\)と二次関数\(y=x^2\)について考えてみます。
一次関数
\(y=3x+1\)

二次関数
\(y=x^2\)
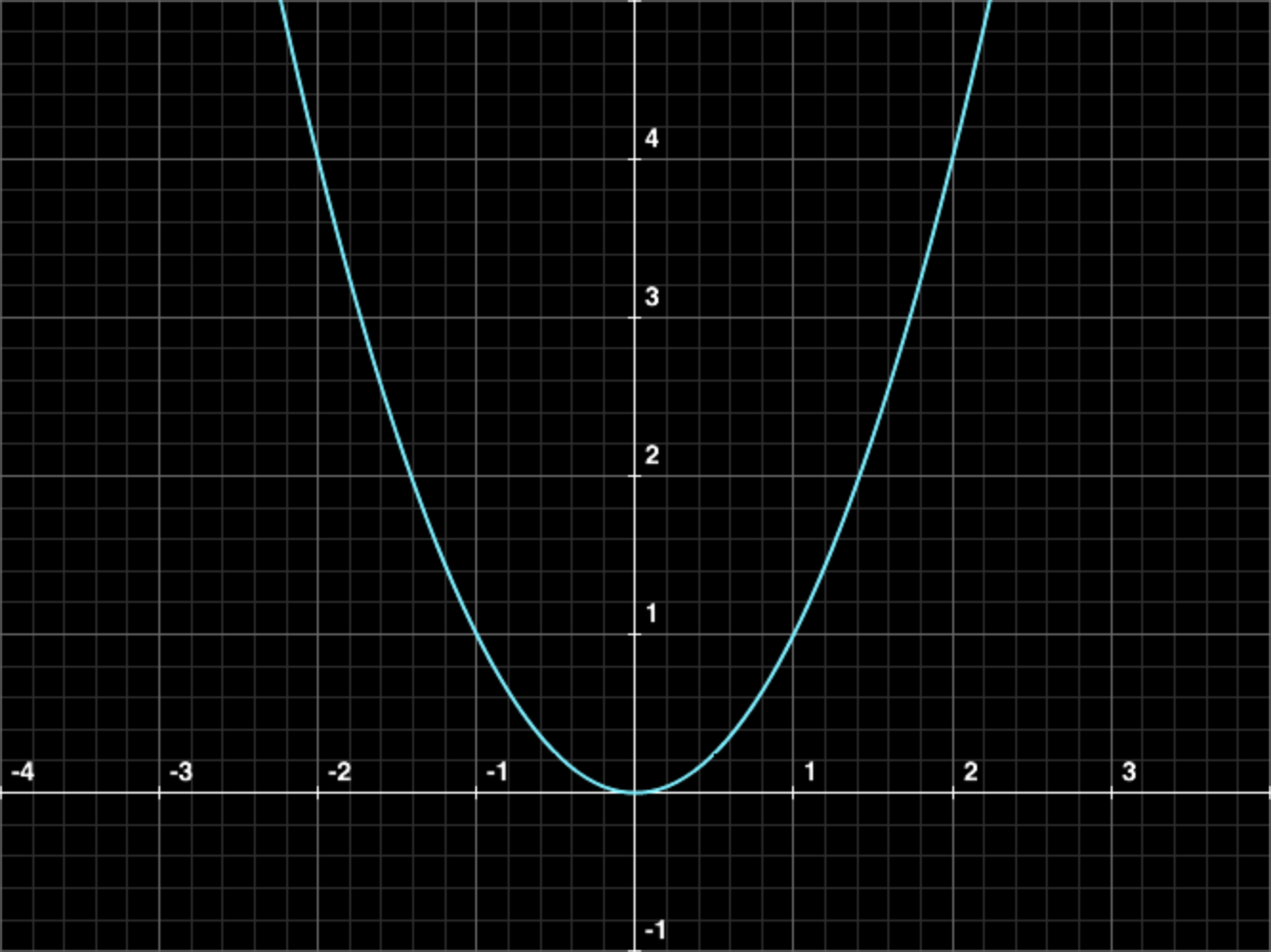
この2つは関数ですので、当然\(x\)の値を1つ決めれば、\(y\)の値も1つに決まります。
では逆に、\(y\)の値を1つ決めた場合はどうでしょうか?




このように同じ関数でも、\(x\)と\(y\)の関数関係を入れ替えてみたときにも関数になるかどうかが異なる場合があります。
一次関数のように「\(y\)は\(x\)の関数」かつ「\(x\)は\(y\)の関数」のような\(x\)と\(y\)の関係を一対一対応といいます。
一対一対応であれば、\(y\)を\(x\)から求めることも、\(x\)を\(y\)から求めることもできます。
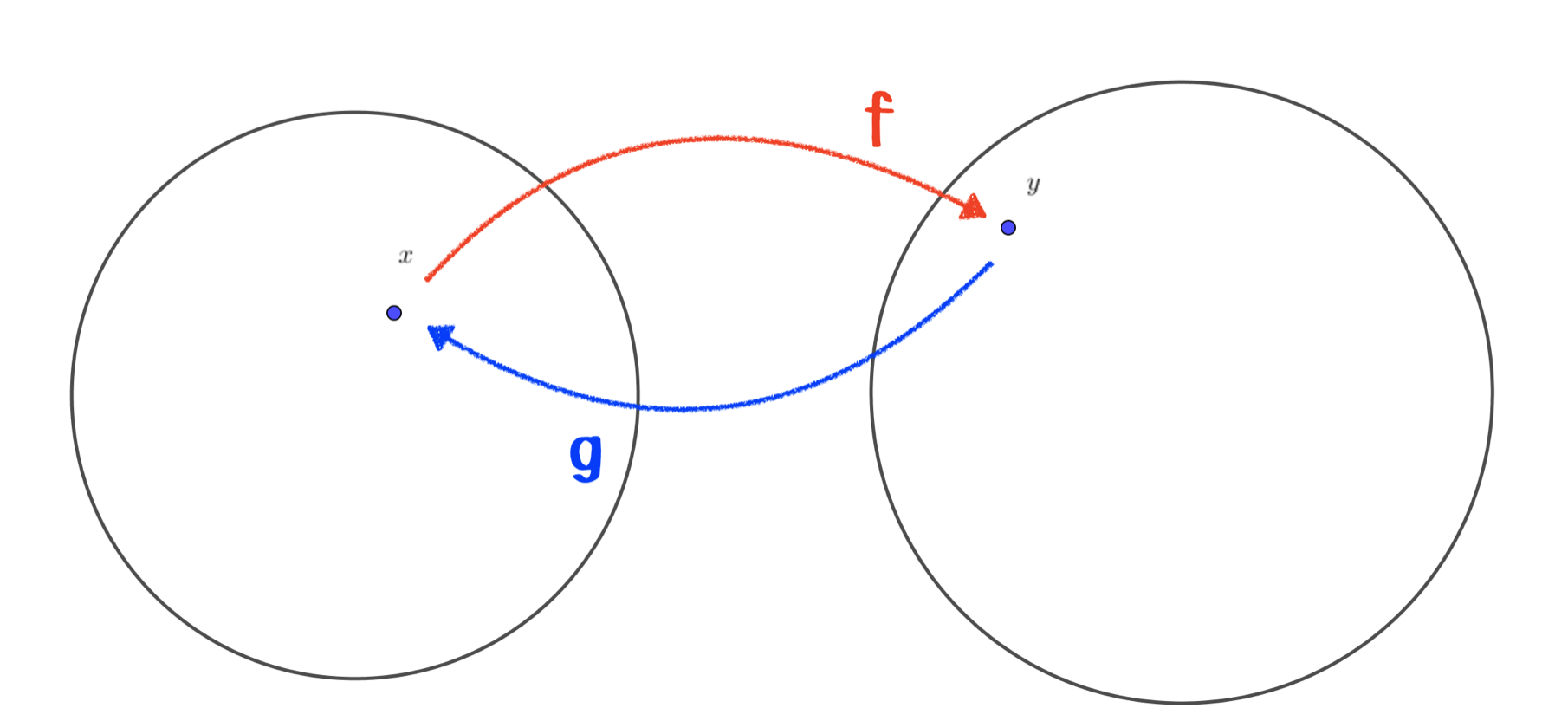
図のように、\(y\)を\(x\)から求める関数\(f\)に対して、\(x\)を\(y\)から求める関数\(g\)のことを\(f\)の逆関数といいます。


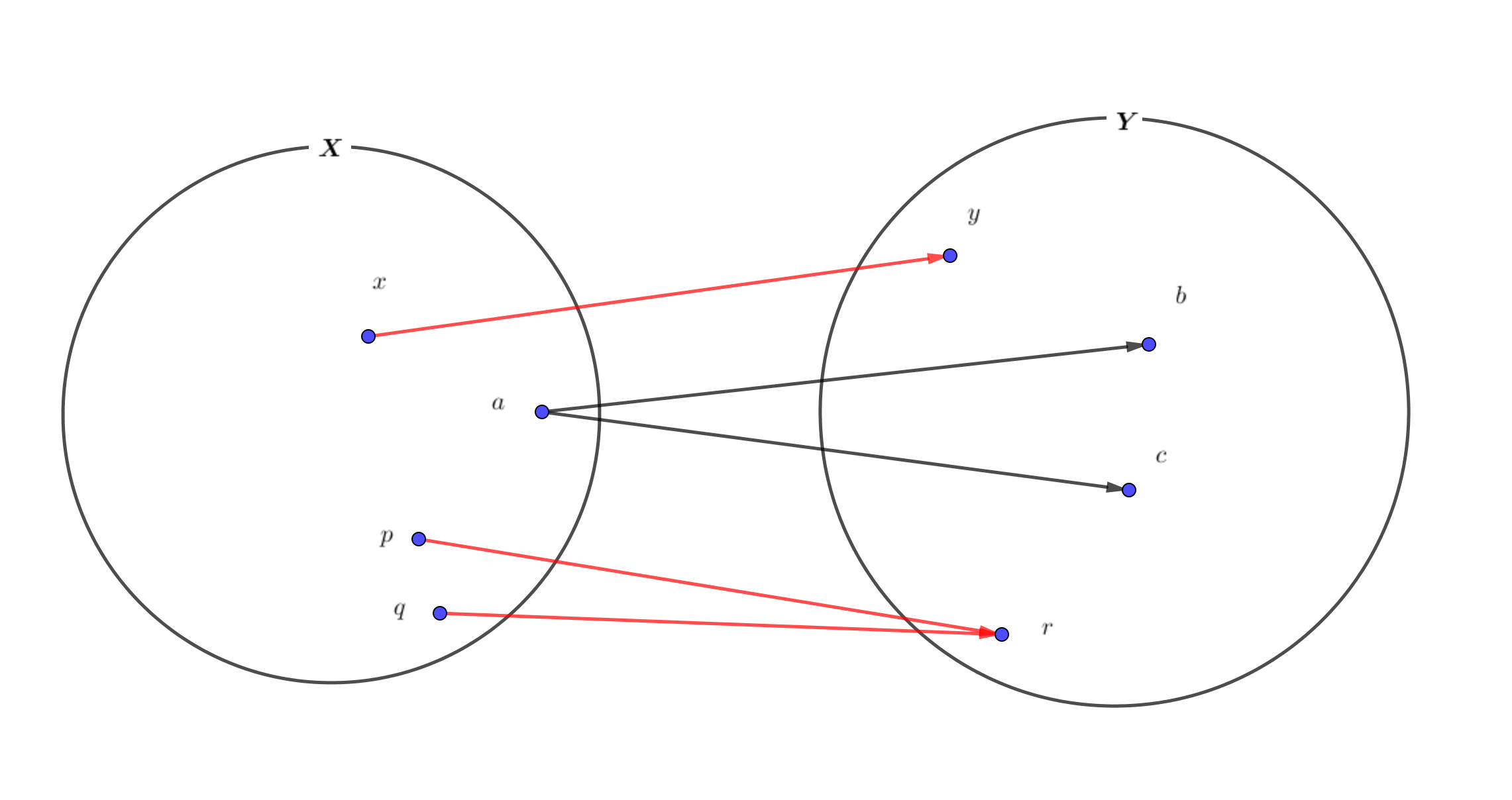

逆関数は一対一対応の場合のみ存在し、従来の関数が「\(x\)1つ決めて\(y\)1つ決まるか」だったのに対して、逆関数は「\(y\)1つ決めて\(x\)1つ決まるか」を考えているということがポイントです。
また、次のような表記も覚えておきましょう。
ポイント
- \(y=f(x)\):「\(y\)は\(x\)の関数」
- \(y=f^{-1}(x)\):「\(x\)は\(y\)の逆関数」
逆関数講座|逆関数の有無の判別


例題
\(y=2x^3+x^2-3x\)は逆関数が存在するか。
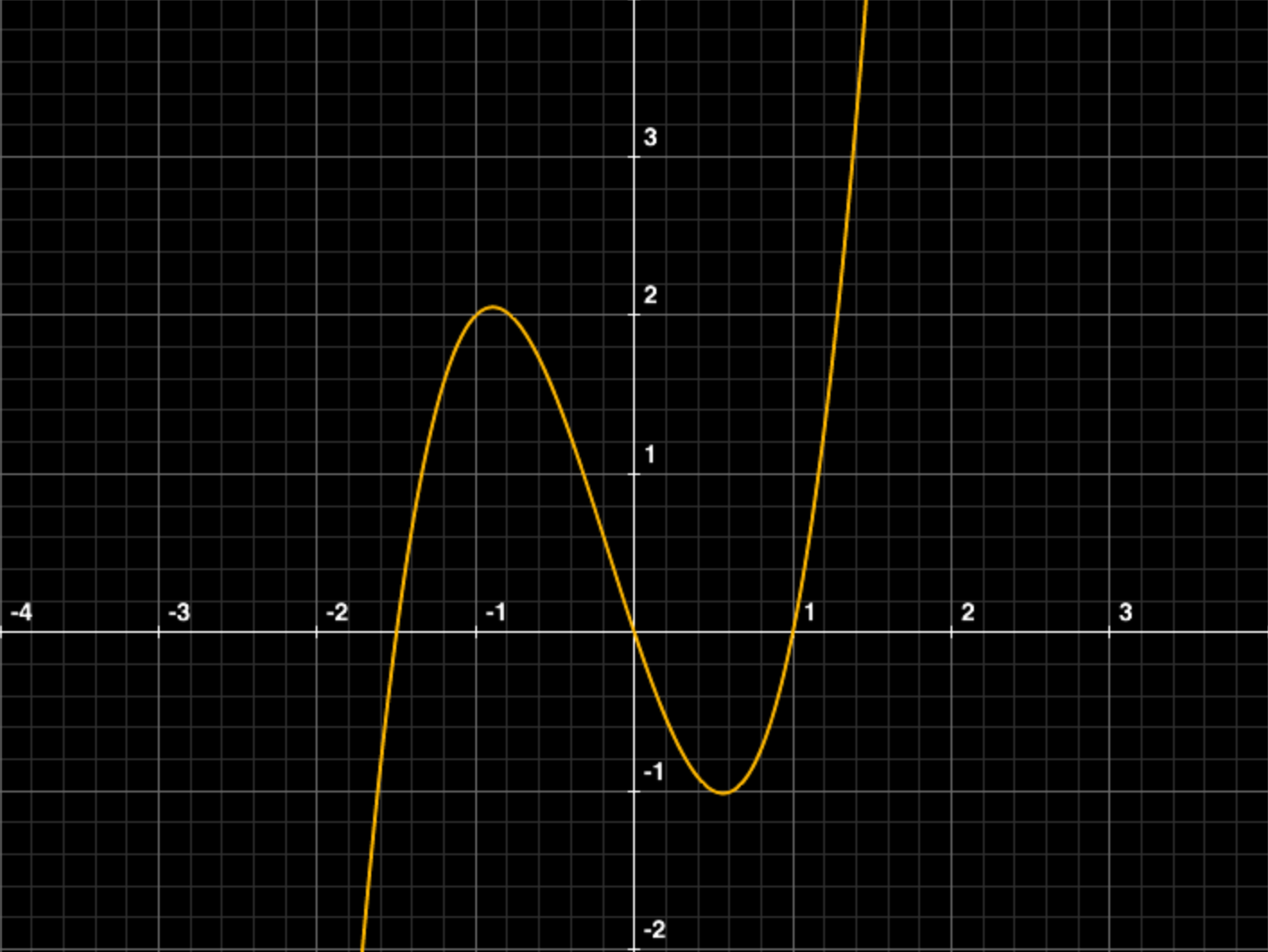




例題
\(y=\log_{10} x\)\((x>0)\)は逆関数が存在するか。
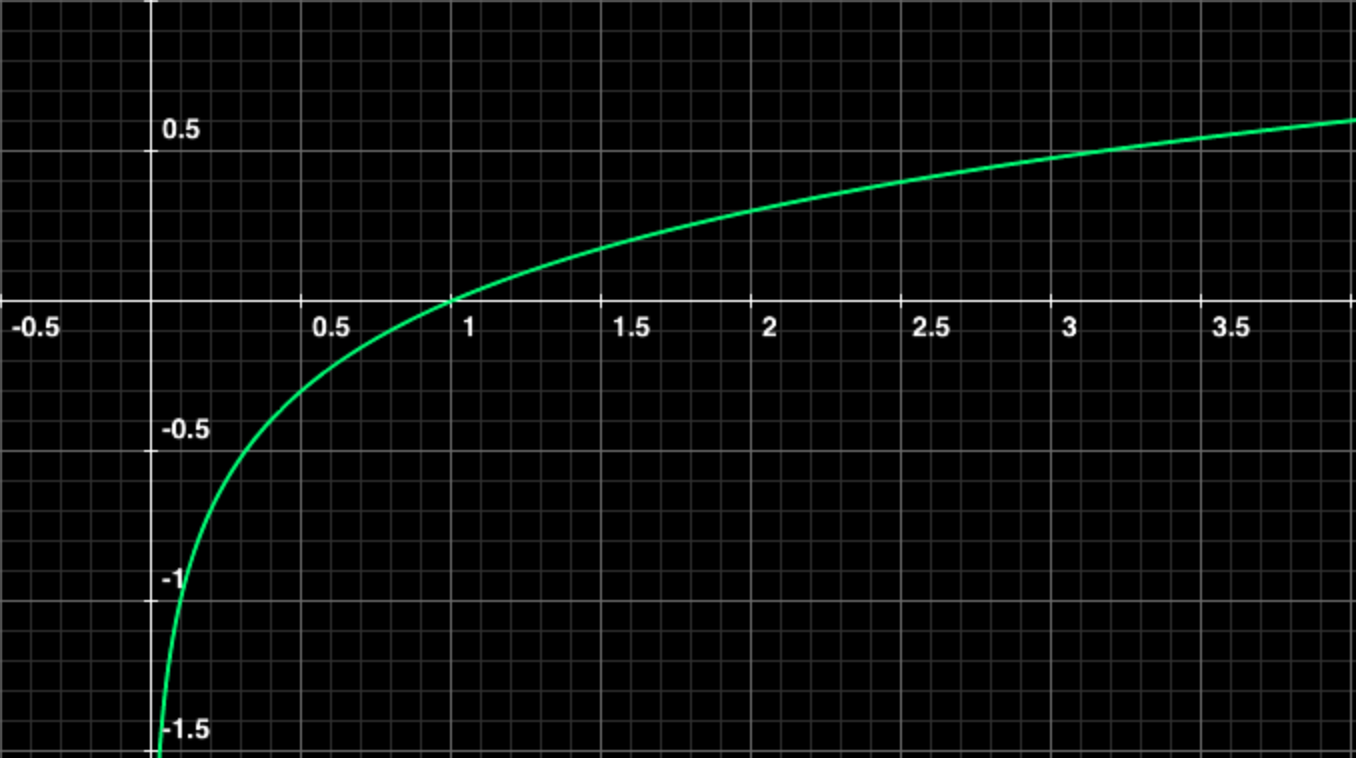


例題
\(y=\sin x\)の逆関数は存在するか。
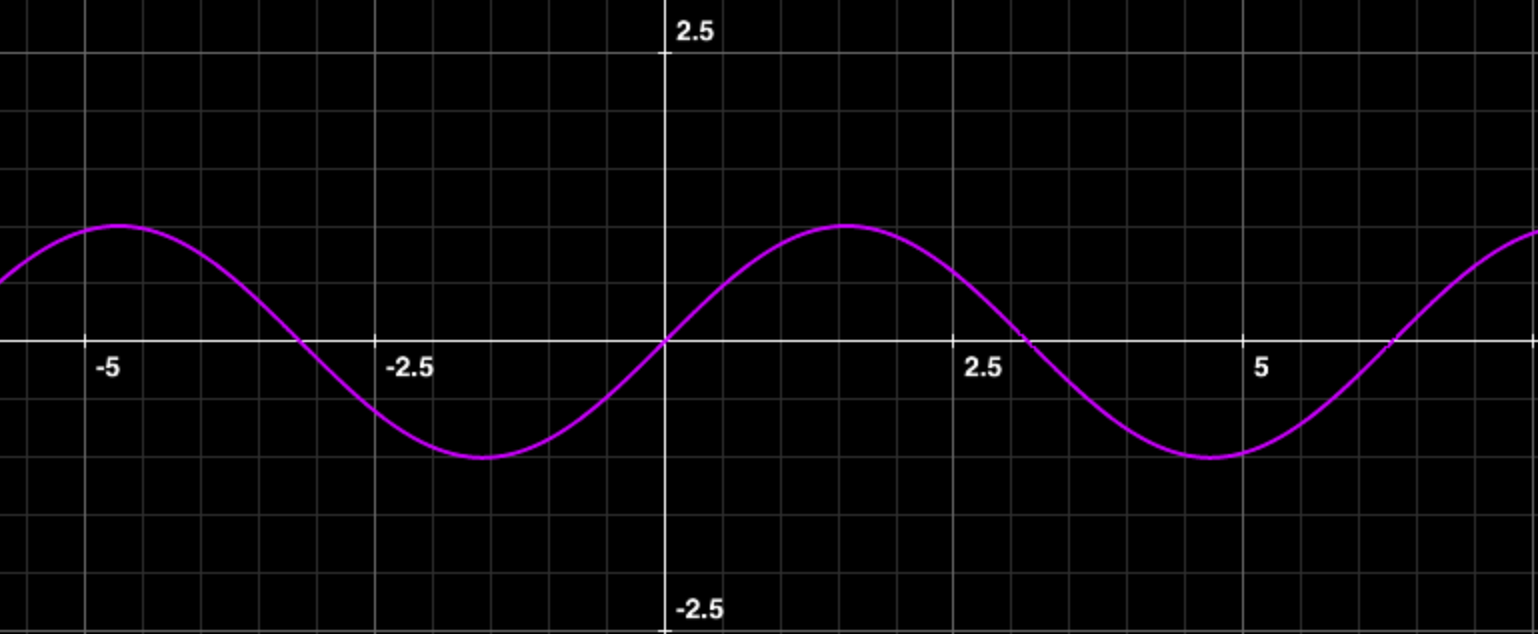


例題
\(y=\sin x (0<x<\frac{\pi}{2})\)の逆関数は存在するか。
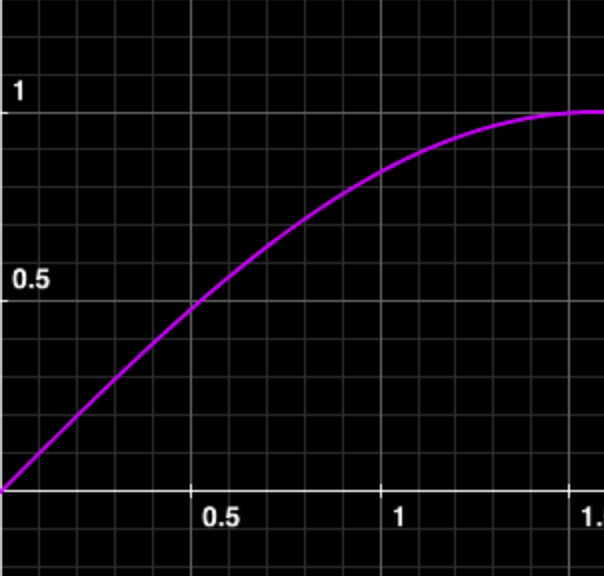


逆関数講座|逆関数の求め方

例題
\(y=\log_{10}x\)の逆関数を求めよ。


\(y=\log_{10} x\iff 10^y=x\)
よって\(x=10^y\)。


ここで\(x\)と\(y\)を入れ替えて、\(y=10^x\)。

逆関数講座|『xとyを入れ替えて』の意味は『x-y座標に合わせて』

ではこの『入れ替える』意味について考えていきましょう。
\(y=\log_{10}x\)、\(x=10^y\)のグラフは両方とも同じグラフのことを指しています。

ところが、見る順番が異なります。
\(y=\log_{10}x\)
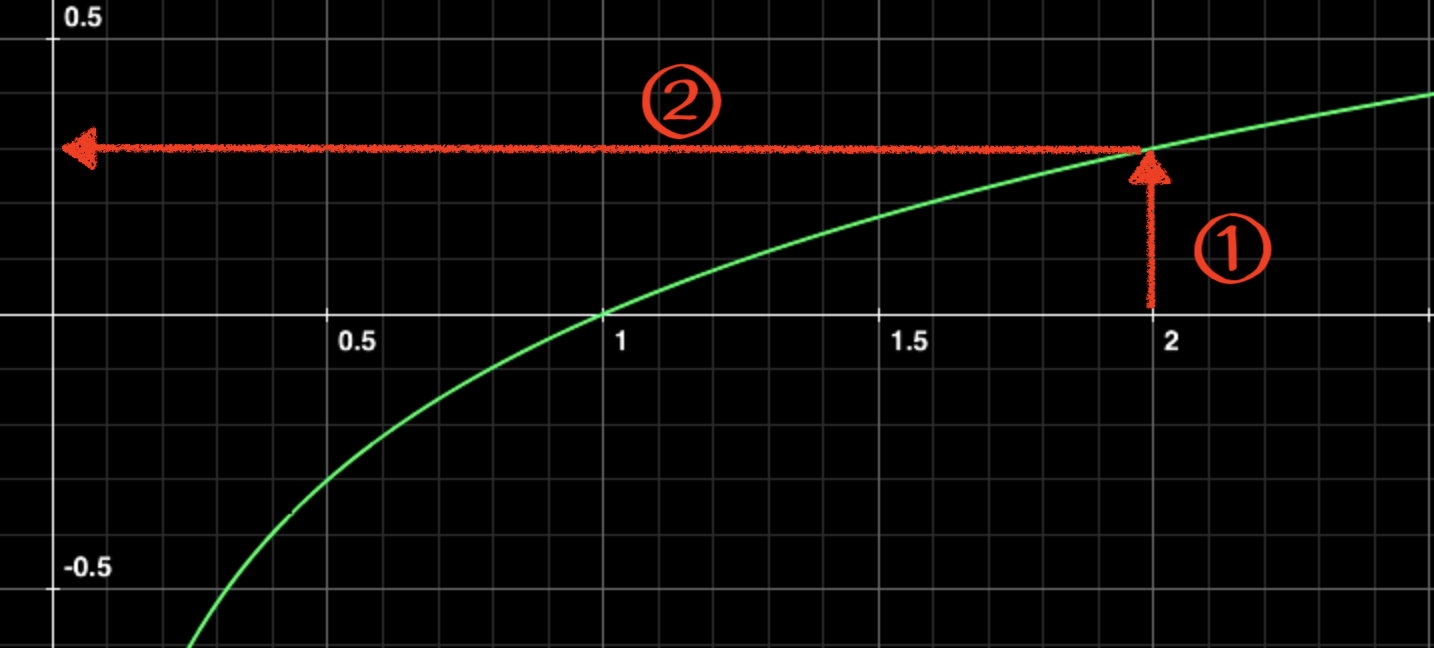
\(x=10^y\)
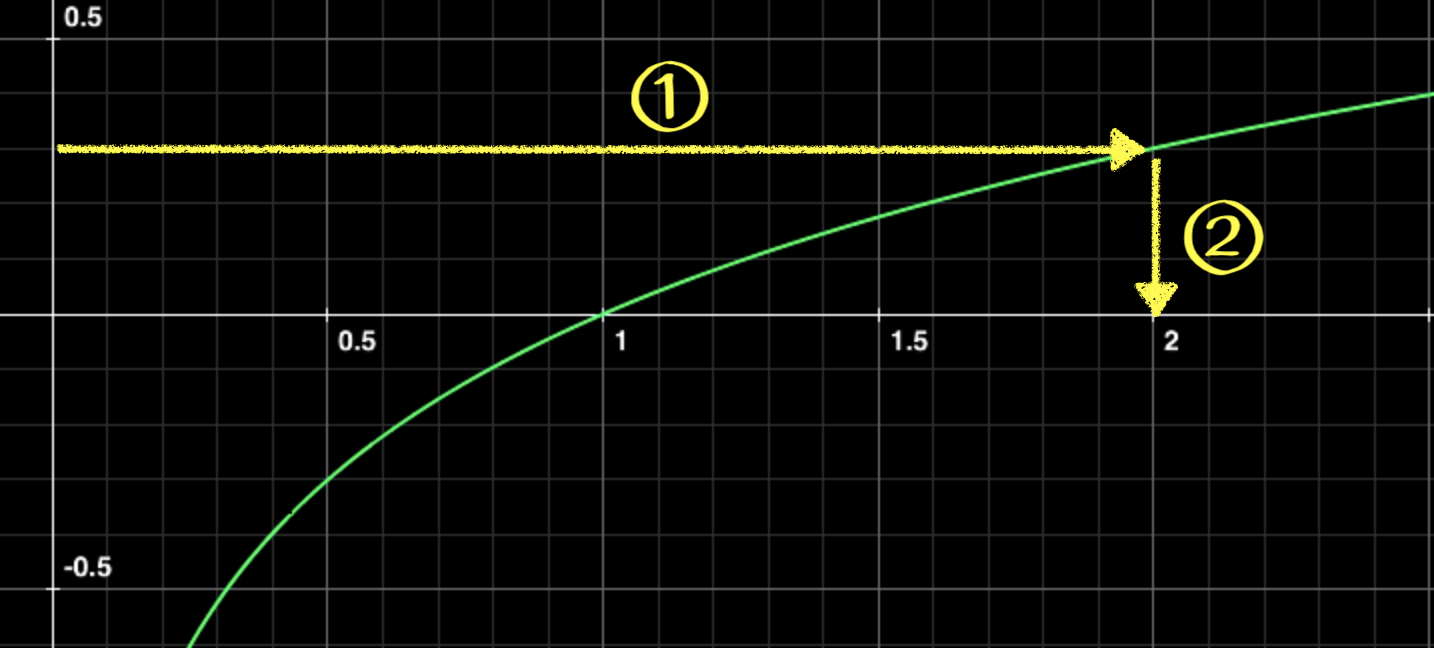
「\(y\)が\(x\)の関数である」とき、\(x\)のことを独立変数、\(y\)のことを従属変数と言いました。
そしてこのとき利用する座標が、いつもよく利用する\(x-y\)座標と呼ばれるものです。
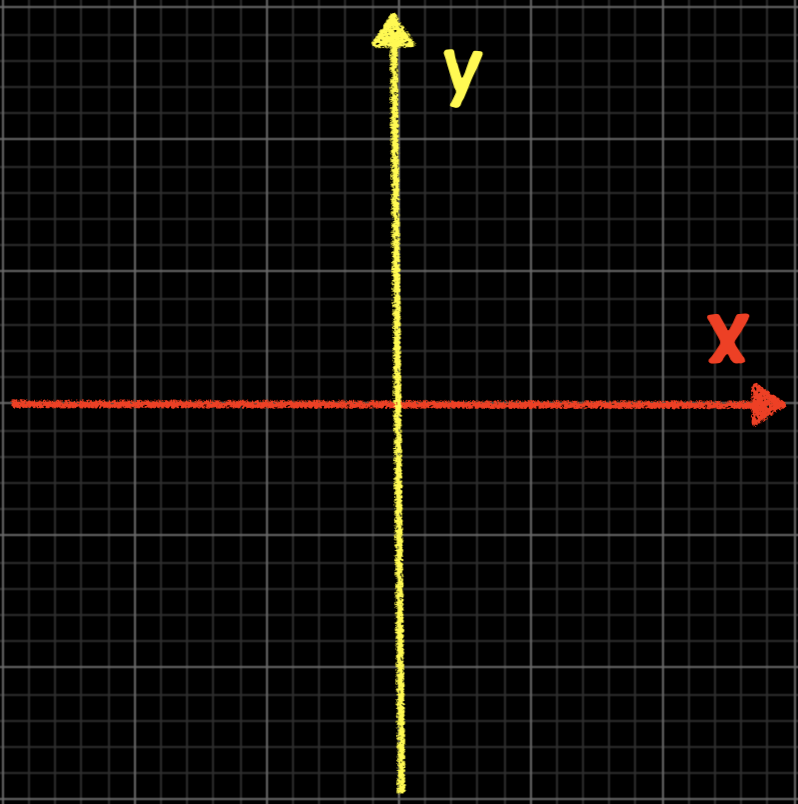

であるならば「\(x\)が\(y\)の関数である」とき、\(y\)のことを独立変数、\(x\)のことを従属変数と言うはずです。
つまりこのとき利用する座標は、\(y-x\)座標のはず。
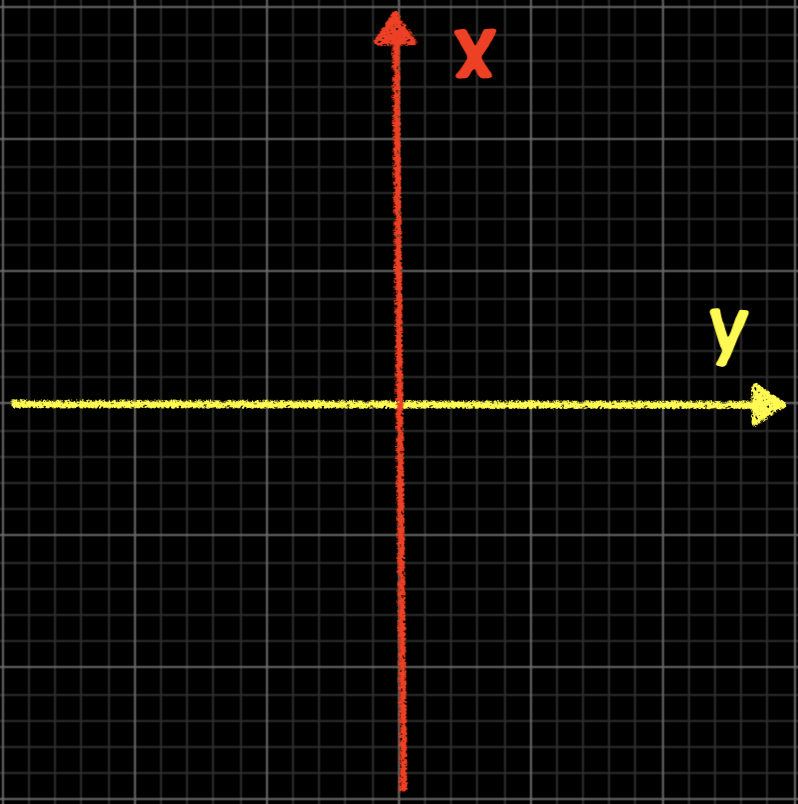
要するに\(x=10^y\)は、横軸が\(y\)、縦軸が\(x\)の座標上にグラフを書いていることを意識しているのです。
ただ、普段使っている\(x-y\)座標を使っている私たちにとって、\(y-x\)座標のままというのは少し不便です。
なぜなら横軸が\(x\)、縦軸が\(y\)という共通認識があるから。
であるならば、\(y-x\)座標の縦軸と横軸の文字を入れ替えてあげれば済みますね。

逆関数講座|逆関数の性質

逆関数の性質① 関数とその逆関数の合成関数は独立変数に戻る。
関数\(f\)に対して、逆関数\(f^{-1}\)はこのようなイメージでした。

このイメージを元に合成関数を考えてみると、合成関数\(f^{-1}\left(f(x)\right)\)は\(x→y→x\)の流れを表していることになります。

合成関数について復習したい人はこちらを参考にしてください。
続きを見る

【合成関数の微分法】のコツと証明→「約分」感覚でOK!小学生もできます。
つまり独立変数\(x\)が関数\(f\)によって従属変数\(y\)に行き着くも、そこから逆関数\(f^{-1}\left(\right)\)によって独立変数\(x\)に戻されているということです。
実際に問題で確かめてみましょう。
例題
関数\(f(x)=\log_{10}x\)のとき、逆関数\(f^{-1}(x)=10^x\)となる。このとき、合成関数\(f^{-1}\left(f(x)\right)\)を求めよ。
(解答)
\begin{align} f^{-1}\left(f(x)\right) &= 10^{\log_{10}x}\\\ &= x\\\ \end{align}




対数の法則について復習したい人はこちらを参考にしてください。
続きを見る



log(ログ)って何?常用対数、自然対数とは?対数を徹底解説!!
逆関数の性質② グラフが\(y=x\)を軸として線対称になっている。
先ほどの関数\(f(x)=\log_{10}x\)とその逆関数\(f^{-1}(x)=10^x\)のグラフを同じ座標上に書いてみるとこのようになります。
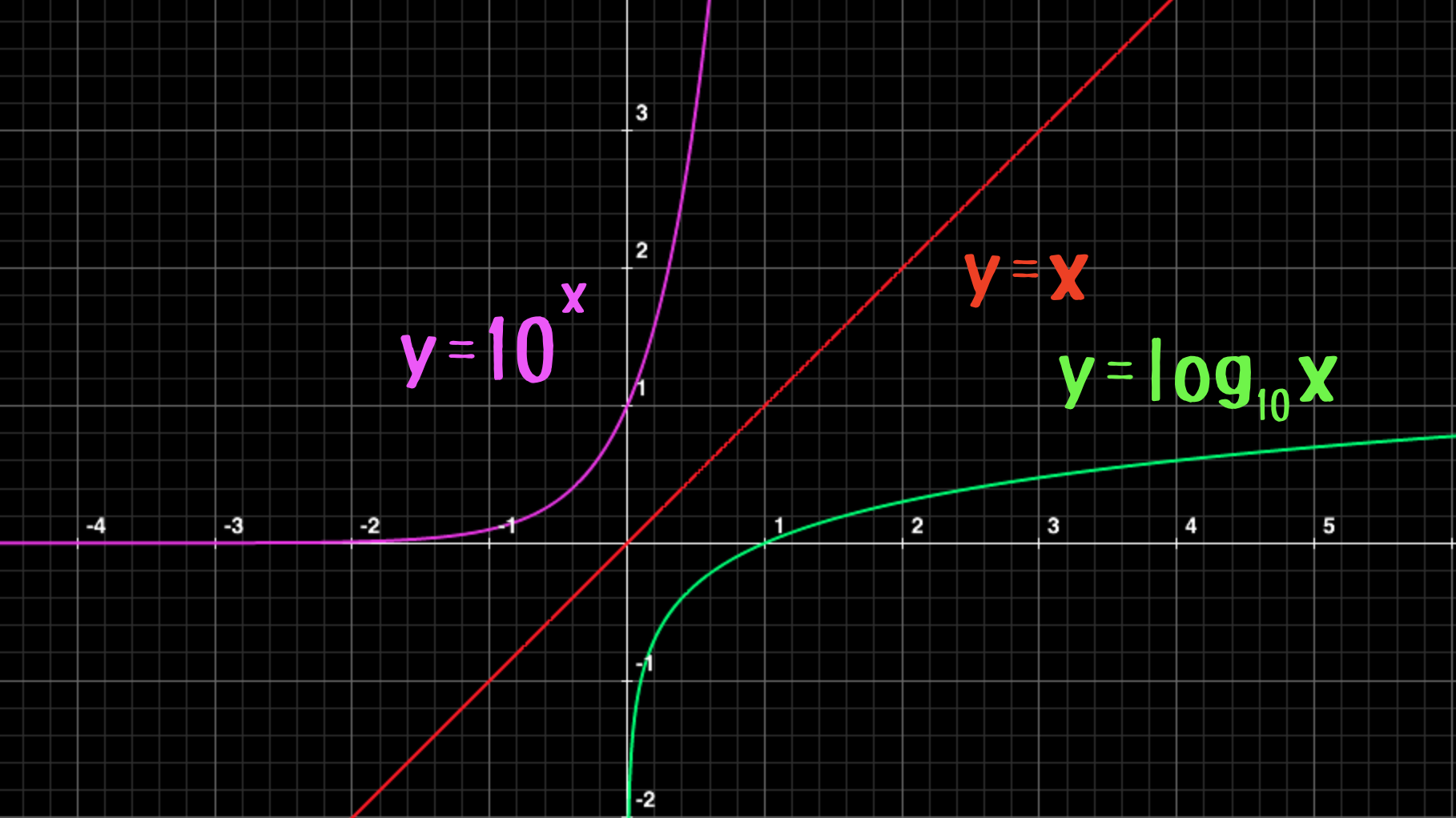



このようになる理由は、非常に単純です。
逆関数では\(y-x\)座標を\(x-y\)座標に書き換える際、\(x\)軸と\(y\)軸をクルッと回転させるような動作がありました。
これは、グラフ上では\(y=x\)と線対称の位置に動かしていることを表しているのです。
逆関数講座|まとめ


まとめ
- \(x\)と\(y\)が一対一のときのみ、逆関数は存在する。
- 逆関数を求めるためには、関数\(y=f(x)\)を\(x=(yの式)\)の形にし、最後に\(x\)と\(y\)を入れ替えれば良い。
今回は特に本質の意味理解が重要でした。
逆関数が存在するための条件、そして逆関数を求める最後になぜ\(x\)と\(y\)を入れ替えるのか、しっかりと理解しておきましょう。
以上、「逆関数について」でした。
チェック問題
例題
関数\(y=7^x\)の逆関数を求めよ。
指数関数なので、逆関数は対数関数であることはわかっていますが、自力で求める練習をしてみましょう。
\(y=7^x\)なので
が成り立ちます。
\(x\)と\(y\)を入れ替えて、
例題
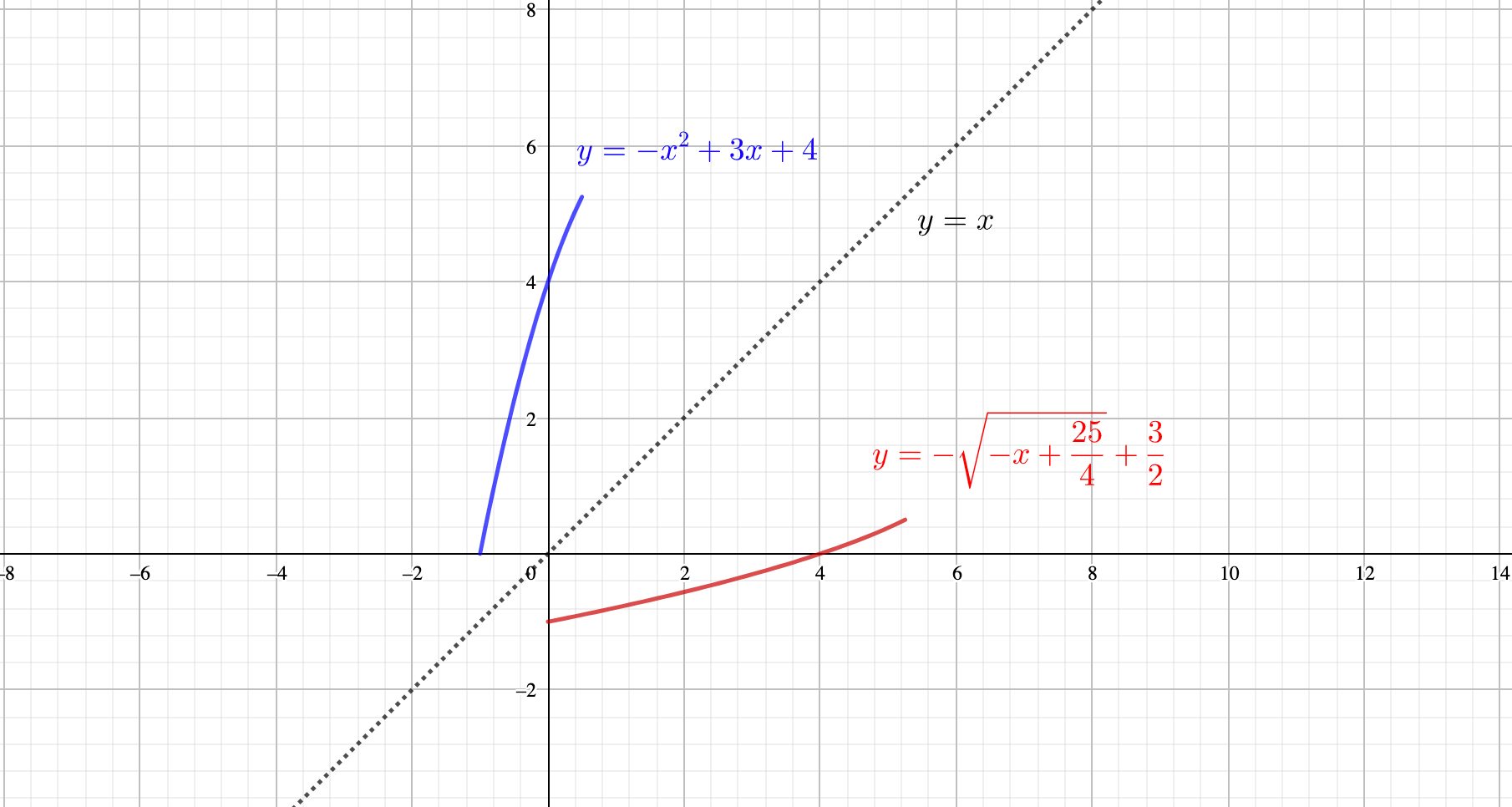
\(y = -x^2 + 3x +4\ (-1< x < \frac{1}{2})\)のとき、逆関数を求めよ。
グラフを見てみると、とりあえず逆関数を考えることはできそうです。
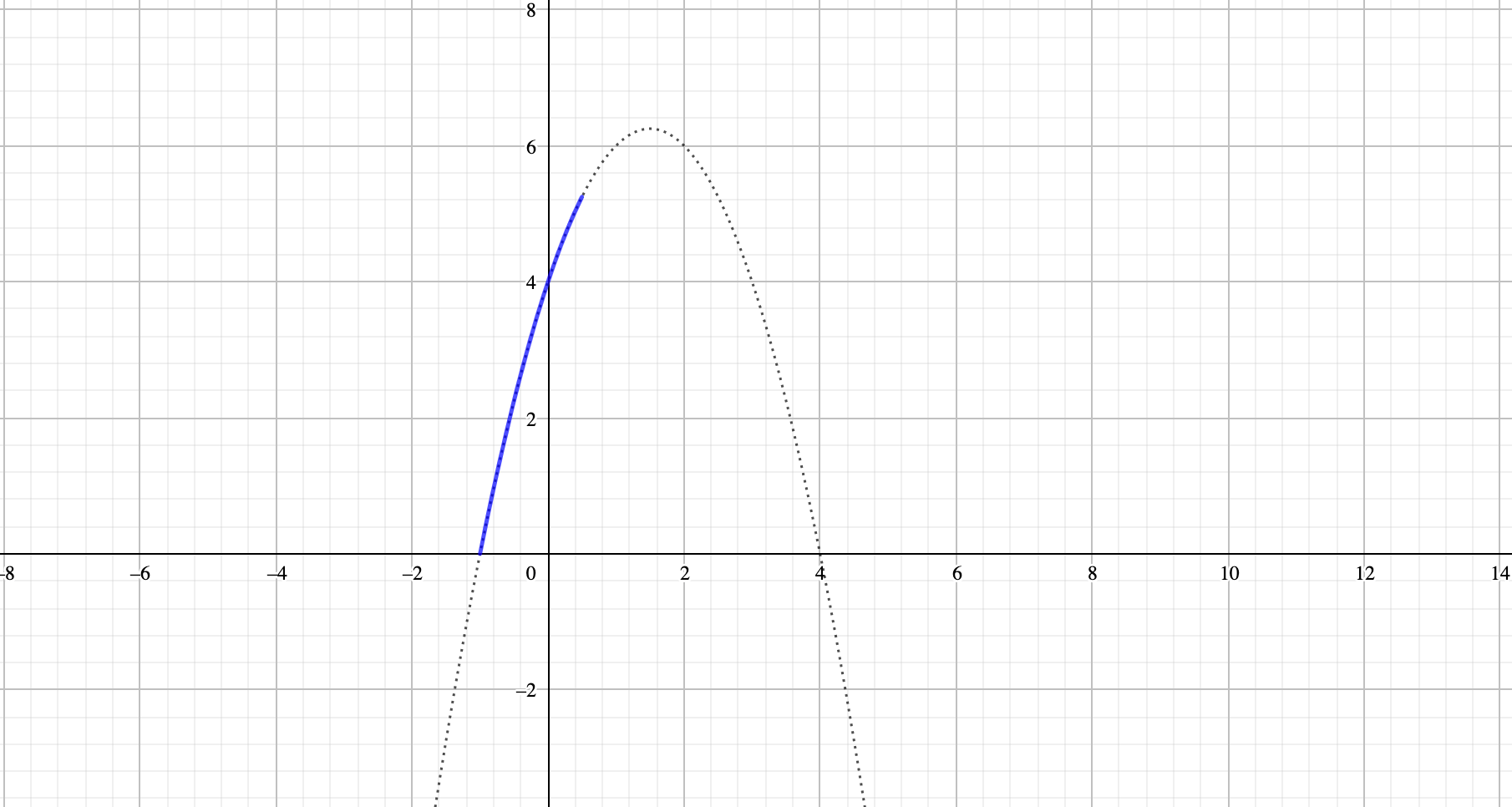

では\(x\)と\(y\)を入れ替える段階まで式変形していきましょう。
(※見切れている場合はスクロール)


参考【平方完成】中学数学から解説!公式の意味と変形の仕方→無理やり二乗を作ると、グラフの動きがわかる!
よって、
ここから「\(x= (yの式)\)」の形を目指して変形していきます。
まずは\(-\left(x-\frac{3}{2}\right)^2\)と\(y\)を移項して
ここで与えられた式には定義域\(-1< x < \frac{1}{2}\)が定められていました。
このとき、\(y\)の値域は\(0< y < \frac{21}{4} \)となります。
つまり\(0 < -y + \frac{25}{4}\)は明らかなので、両辺にルートを取ることができます。
よって、


よって、
が求められます。


\(0< y < \frac{21}{4} \)より\(1< -y + \frac{25}{4} < \frac{25}{4} \)なので、
これをもとに考えると、条件\(-1< x < \frac{1}{2}\)に合致するのは、
のみとわかります。
「\(x= (yの式)\)」の形になりましたので、\(x\)と\(y\)を入れ替えて