【べき乗の微分公式】x^nの微分は実は難しい。知ってれば差がつく公式証明

Today's Topic

$$\left(x^n\right)'=nx^{n-1}$$

楓

今日は最も基本的な微分公式、べき乗の微分公式について考えるよ。

そんなに難しい内容かな？指数を前に出して、1引けばいいんじゃないの？

小春

楓

じゃあ、$n$が負のときや実数のときは成り立つのかな？

えっ、成り立ちそうだけど。。。証明はできないなぁ・・・。

小春

楓

今回は学校で疎かにされがちな、数学の発展性に着目して、レベルアップしていこう！

この記事を読むと、この意味がわかる！

$\left(x^n\right)'=nx^{n-1}$の証明
数学の発展的な考え方

Contents

1 準備1：微分の定義
2 準備2：数の集合
3 数ⅡBべき乗の微分：自然数のとき→二項定理を使おう
4 数Ⅲべき乗の微分：整数のとき→負の場合を考えてみよう
5 数Ⅲべき乗の微分：有理数のとき→逆関数の微分法を活用する
6 数Ⅲべき乗の微分：実数のとき→対数微分法を活用する
7 まとめ

準備1：微分の定義

楓

ここで微分のイメージを軽く復習しておきましょう。

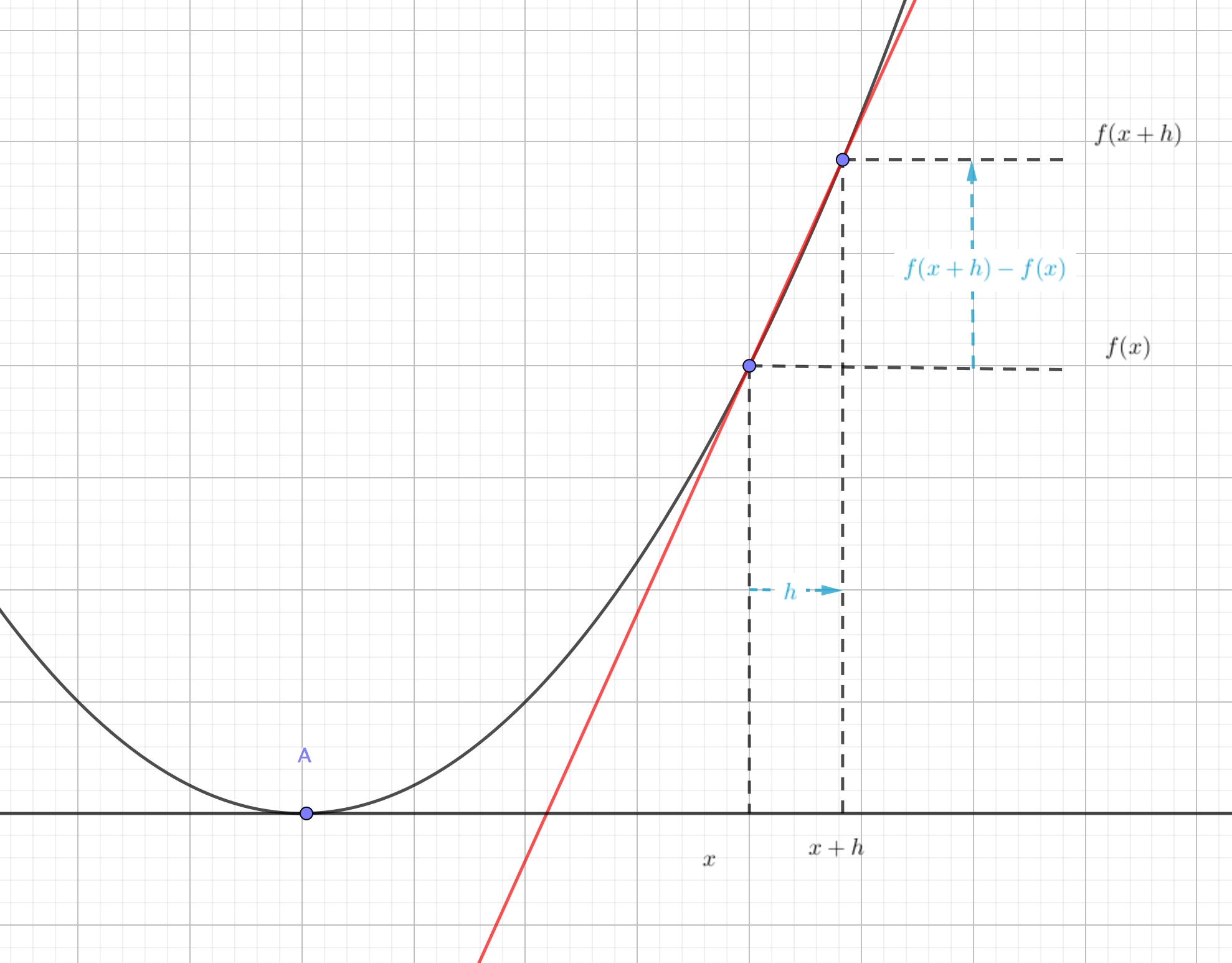
微分の一般的な定義は

ポイント

$$\lim_{h\rightarrow 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}$$

でした。

これはグラフ上の適当な点と、その点から$x$座標が$h$だけ増えたもう一点を結んだ直線を意識していましたね。

準備2：数の集合

今回に限らず言えることですが、高校数学では数の集合がかなり重要になります。

今回も自然数や整数、実数と、それぞれ異なる性質を持つ数の特徴を、よく考えてあげなければなりません。

『数の集合怪しいなぁ・・・』

という人は今一度、簡単でもいいので復習して見ることをオススメします。

楓

マジで理解度が圧倒的に深まるぞ！！

参考【数の集合】自然数とは？整数とは？感覚だけでわかる数の集合

数ⅡBべき乗の微分：自然数のとき→二項定理を使おう

まずは、

疑問

$n$が自然数のとき、

$$\left(x^n\right)'=???$$

について考えます。

微分の定義を用いると、

$$f'(x)=\lim_{h\rightarrow 0}\frac{\left(x+h\right)^n-x^n}{h}$$

と表せますね。

しかし$\left(x+h\right)^n$が少々厄介です。分子をもっと簡単にしなければ、これは解けません。

そこで二項定理と呼ばれるものを用います。

ポイント

$(x+a)^n={}_nC_0x^0a^n+{}_nC_1x^1a^{n-1}+{}_nC_2x^2a^{n-2}+\cdots +{}_nC_{n-1}x^{n-1}a^1+{}_nC_nx^na^0$

（※見切れている場合はスクロール）

参考【差がつくポイント】二項定理はイメージで覚えろ！重要なポイントと活用場面を総まとめ！

これを用いると分子は次のように変形できます。

\begin{align} （分子）&= \left(x+h\right)^n-x^n\\\ &=\left( {}_nC_0x^0h^n+{}_nC_1x^1h^{n-1}+\cdots +{}_nC_{n-1}x^{n-1}h^1+{}_nC_nx^nh^0\right)-x^n\\\ &= {}_nC_{0}h^n+{}_nC_{1}nh^{n-1}x+\cdots+{}_nC_{n-1}hx^{n-1}\\\ &= h\left({}_nC_{0}h^{n-1}+{}_nC_{1}nh^{n-2}x+\cdots+{}_nC_{n-1}x^{n-1}\right)\\\ \end{align}

（※見切れている場合はスクロール）

よって

\begin{align} f'(x) &= \lim_{h\rightarrow 0}\frac{\left(x+h\right)^n-x^n}{h}\\\ &= \lim_{h\rightarrow 0}\frac{h\left({}_nC_{0}h^{n-1}+{}_nC_{1}nh^{n-2}x+\cdots+{}_nC_{n-1}x^{n-1}\right)}{h}\\\ &= \lim_{h\rightarrow 0}\left({}_nC_{0}h^{n-1}+{}_nC_{1}nh^{n-2}x+\cdots+{}_nC_{n-1}x^{n-1}\right)\\\ &= {}_nC_{n-1}x^{n-1}\\\ &= nx^{n-1}\\\ \end{align}

（※見切れている場合はスクロール）

となり、次の微分公式が得られます。

微分の定義と二項定理を組み合わせると、最終的に$ {}_nC_{n-1}x^{n-1}$の項しか残らない

$$\left(x^n\right)'=nx^{n-1}(nは自然数)$$

ただしここで注意して欲しいのは、二項定理を用いている点です。

二項定理は$n$が自然数のときにしか使えないという制約があるため、この微分公式は今のところ自然数でしか成り立ちません。

小春

結局、整数とか自然数では成り立たないの？

ううん、ちゃんと成り立つよ。ここから順を追って見ていこう！

楓

数Ⅲべき乗の微分：整数のとき→負の場合を考えてみよう

ここでは、

疑問

$n$が整数のとき、

$$\left(x^n\right)'=???$$

を考えます。

今の状況では、自然数であれば微分公式

$$\left(x^n\right)'=nx^{n-1}(nは自然数)$$

を使うことができます。

指数$n$が整数になっても、この微分公式は成り立つのですが、それには証明が欠かせません。

証明するためには、『$n$が負の整数でも成り立つ』ということを証明します。

証明方法は至ってシンプル。

先ほど手に入れた微分公式の指数$n$が負の数であることを仮定します。

考えること

$$\left(x^n\right)'(n<0)$$

ここで、

$$n=-m\ (mは正の整数)$$

と置きます。

すると、次のような式変形が行えます。

\begin{align} \left(x^n\right)' &=\left(x^{-m}\right)'\\\ &= \left(\frac{1}{x^m}\right)'\\\ \end{align}

ここで、商の微分公式を使います。

ポイント

$$\left(\frac{1}{f(x)}\right)'=-\frac{f'(x)}{\left(f(x)\right)^2}$$

参考【分数関数の微分法】暗記をグッと減らせる！分数の微分が思考停止2秒で解ける！

すると・・・。

\begin{align} \left(\frac{1}{x^m}\right)' &= -\frac{\left(x^m\right)^2}{x^{2m}}\\\ &= -\frac{mx^{m-1}}{x^{2m}}\\\ &= -mx^{(m-1)-2m}\\\ &= -mx^{-m-1}\\\ &= nx^{n-1}\\\ \end{align}

楓

最後に$-m$を$n$に戻すよ！

これで$n$が負の整数のときでも、べき乗の微分公式が成り立つことがわかりました。

また、$n=0$を代入しても成り立つことから、

$$\left(x^n\right)'=nx^{n-1}\, \color{red}{(nは整数)}$$

と、より数の世界を広げて考えることができました。

数Ⅲべき乗の微分：有理数のとき→逆関数の微分法を活用する

さて、お次は

疑問

$n$が有理数のとき、

$$\left(x^n\right)'=???$$

を考えます。

どんな有理数も正の整数$p$と、特の条件のない整数$q$によって、$\frac{q}{p}$を表されます。

つまりここでは、

$$n=\frac{q}{p}\ (pは正の整数、qは整数)$$

と置き、

$$y=x^{\frac{q}{p}}$$

について考えれば良いわけです。

ここから先は、少し大変なので3ステップに分けて考えていきます。

step
1$x^{\frac{1}{p}}$の微分を考える

まずは簡単にするために、

$$y=x^{\frac{1}{p}}$$

について考えます。

これを両辺$p$乗すると、

$$y^p=x$$

となり、左辺と右辺を入れ替えて、

$$x=y^p$$

としておきましょう。

ここで、両辺$y$で微分してあげます。

すると、

\begin{align} \frac{dx}{dy} &= \frac{y^{p}}{dy}\\\ &= py^{p-1}\\\ \end{align}

となりますね。

求めたい$\frac{dy}{dx}$の値は、ここから逆関数の微分法を使って求めます。

ポイント

$$ \frac{dy}{dx} = \frac{1}{\frac{dx}{dy}}$$

参考【逆関数の微分法】って結局いつ使うの？証明や使い方をわかりやすく紹介

\begin{align} \frac{dy}{dx} &= \frac{1}{\frac{dx}{dy}}\\\ &= \frac{1}{py^{p-1}}\\\ \end{align}

小春

あれ、、でも右辺にまだ$y$がいるよ。。。

そう、この$y$を$x$の式に戻したら完成！

楓

得られた式の$y$を$x^{\frac{1}{p}}$に戻します。

\begin{align} \frac{1}{py^{p-1}} &= \frac{1}{p\left( x^{\frac{1}{p}}\right)^{p-1}}\\\ &= \frac{1}{px^{1-\frac{1}{p}}}\\\ &= \frac{1}{p}x^{\frac{1}{p}-1}\\\ \end{align}

これにより、

$$\left(x^{\frac{1}{p}}\right)'=\frac{1}{p}x^{\frac{1}{p}-1}$$

とわかりました。

$y=x^{\frac{1}{p}}$は両辺$p$乗して逆関数の微分法を使うと求められる。

step
2$x^{\frac{q}{p}}$の微分を考える

では、$y=x^{\frac{q}{p}}$の微分を考えていきましょう。

ここで合成関数の微分法を導入します。

ポイント

$$\frac{dy}{dx}=\frac{dy}{du}\times\frac{du}{dx}$$

参考【合成関数の微分法】のコツと証明→「約分」感覚でOK！小学生もできます。

まず、$y=x^{\frac{q}{p}}$を

$$y=\left(x^{\frac{1}{p}}\right)^q$$

のように、$q$だけくくり出した形を作ります。

そして$x^{\frac{1}{p}}$を適当な文字$u$に置き換えてみると、

$$ y = u^q,\ u = x^{\frac{1}{p}}$$

となり、それぞれ$u$と$x$で微分すると、

$$\frac{dy}{du} = q\left(x^\frac{1}{p}\right)^{q-1},\ \frac{du}{dx} = \left(x^\frac{1}{p}\right)'$$

となりますね！

よって合成関数の微分法より、

\begin{align} \frac{dy}{dx} &= \frac{dy}{du} \times \frac{du}{dx}\\\ &= q\left(x^\frac{1}{p}\right)^{q-1} \times \left(x^\frac{1}{p}\right)'\\\ \end{align}

と変形できます。

小春

あ、最後に$\left(x^{\frac{1}{p}}\right)'$が登場したね。

そう、あとはSTEP1の結果を代入するだけだ。

楓

\begin{align} q\left(x^\frac{1}{p}\right)^{q-1}\times \left(x^\frac{1}{p}\right)' &= q\left(x^\frac{1}{p}\right)^{q-1}\times\frac{1}{p}x^{\frac{1}{p}-1}\\\ &= \frac{q}{p}x^{\frac{q}{p}-1}\\\ \end{align}

（※見切れている場合はスクロール）

step
3$\frac{q}{p}$を$n$に戻す

最後に、$\frac{q}{p}=n$に戻すと、

$$\left(x^n\right)'=nx^{n-1} \color{red}{(nは有理数)}$$

が証明できています。

楓

ここが一番大変なポイントだね。

これまで勉強したいろんな微分法が盛り沢山だね・・・。

小春

$y=x^{\frac{q}{p}}$の微分は合成関数の微分法と、STEP1の結果を使って求められる。

数Ⅲべき乗の微分：実数のとき→対数微分法を活用する

いよいよ最後、

疑問

$n$が実数のとき、

$$\left(x^n\right)'=???$$

を考えましょう。

指数関数$y=x^n$は、指数関数の前提条件として$x>0$でしたね（この条件、2回使います）。

参考【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

このおかげで、指数関数の両辺に自然対数を取ることができます。

$$\log y = n\log x$$

小春

$\log x$が考えられるのは、$x>0$の条件があるからだね。

さらに両辺を$x$で微分してあげましょう。

$$\frac{d}{dx} \log y = n \frac{d}{dx} \log x$$

右辺の微分は、対数微分法を用いて解決を試みます。

ポイント

$$\left(\log x\right)'=\frac{1}{x}$$

参考【対数関数の微分公式】証明と式変形のコツ→ネイピア数の定義に帰着

対数微分法を行うことで、

$$n \frac{d}{dx} \log x=\frac{n}{x}$$

が得られますね。

楓

ただし$x>0$の条件があるから、$\frac{○}{x}$を考えられるってこと忘れないでね！！

そうか$x=0$でないことが保証されていることになるから、分母に$x$を持ってこれるのね！

小春

左辺はこれに加え、合成関数の微分法で対処します。

ポイント

$$\frac{dy}{dx}=\frac{dy}{du}\times\frac{du}{dx}$$

参考【合成関数の微分法】のコツと証明→「約分」感覚でOK！小学生もできます。

これにより、次のようなみなし方が可能です。

\begin{align} \frac{d}{dx} \log y &= \frac{dy}{dx} \cdot \frac{\log y}{dy}\\\ &= \frac{y'}{y}\\\ \end{align}

この2つを合わせて考えると、

$$ \frac{y'}{y} = \frac{n}{x}$$

と結構シンプルな形に。

$y$を両辺にかけてあげると、

\begin{align} y' &= \frac{ny}{x}\\\ &= n\frac{x^n}{x}\\\ &= nx^{n-1}\\\ \end{align}

となります。

以上のことから、

$$\left(x^n\right)'=nx^{n-1} \color{red}{(nは実数)}$$

が証明されました。

まとめ

楓

今日は疲れたね。まとめます。

まとめ

べき乗の微分公式が成り立つことを証明するためには、

自然数のとき
整数のとき
有理数のとき
実数のとき

の順に行うと良い。

自然数→二項定理
整数→指数を負とおく
有理数→逆関数・合成関数の微分法
実数→対数微分法

を使えばOK

べき乗の微分法は、最も最初に習う単純そうな公式です。

しかしながらその裏には、数の集合ごとにしっかりとした証明が求められる応用問題でもあります。

これまでの微分法の練習問題として、何度かチャレンジしてみるといいですよ。

楓

もちろん証明方法を覚える必要はないよ。これまで学んだ微分法の練習問題として使って見てね。

以上、「べき乗の微分公式の証明」についてでした。

【べき乗の微分公式】x^nの微分は実は難しい。知ってれば差がつく公式証明

準備1：微分の定義

準備2：数の集合

数ⅡBべき乗の微分：自然数のとき→二項定理を使おう

数Ⅲべき乗の微分：整数のとき→負の場合を考えてみよう

数Ⅲべき乗の微分：有理数のとき→逆関数の微分法を活用する

数Ⅲべき乗の微分：実数のとき→対数微分法を活用する

まとめ

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則