【平均値の定理】結局いつ・どう使うの？使うコツとタイミングを徹底解説

小春

楓くん、平均値の定理ってさ、結局何したいの？

そうだね、微分を使って不等式の条件を考えやすくする、って感じかな。

楓

小春

不等式？じゃあメインは微分じゃなくて不等式なの？！

そんな感じ。じゃあ今回は、平均値の定理が使える不等式の特徴なんかもみていこう！

楓

平均値の定理とは

小春

・・・・ふぇ。

だよね！何のこと言ってるかわかんないよね？！泣かないで汗

楓

平均値の定理の意味

公式の意味は、実は至ってシンプル。

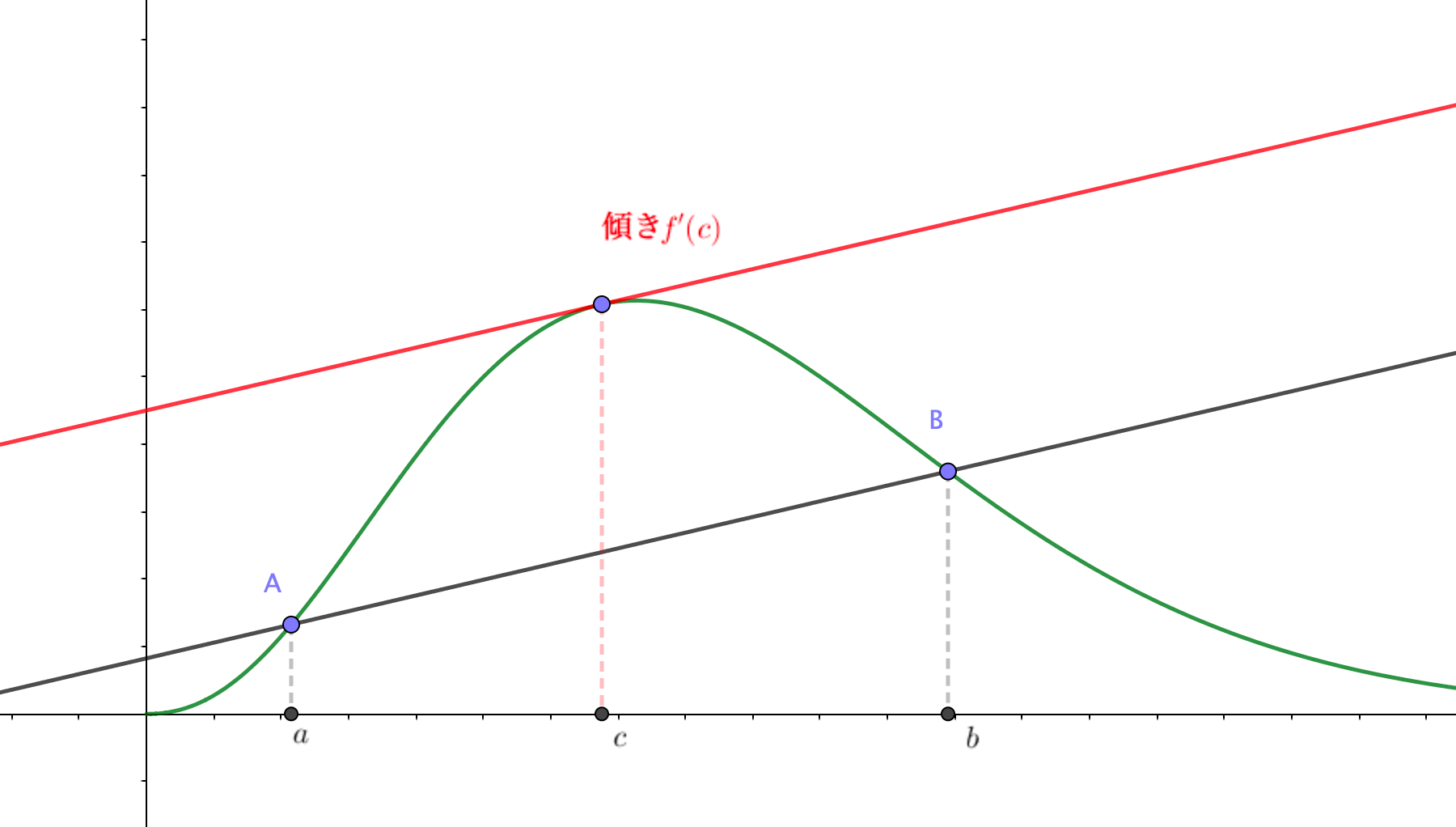
って言っています。

小春

う～ん、図を見ればなんかわかる気はする・・・。

証明は大学数学でやるから、いったんパスでOK。

楓

小春

でもこれ、いったい何に使うの？？

平均値の定理を使うコツ

平均値の定理は、微分の問題で登場することはほぼありません。

小春

じゃあいつ使うの？

平均値の定理を使う場面、それは不等式の問題です。

楓

微分の問題で使うのではなく、不等式を解く手法に微分を取り入れたって感じかな。

例題を見る前に結論から言っておくと、平均値の定理は不等式内に

が登場しているときに使える場合が多いです。

では例題を見ていきましょう。

平均値の定理の例題

ここでは標準・応用の2問を通して、平均値の定理の使い方を紹介します。

結局、平均値の定理が使えるようにゴリ押して、不等式を証明すればOKです。

平均値の定理の例題（標準）

小春

む、、、\(b-a\)がいる・・・。

ではまず、\(f(x)=\sin x\)と置きます。

すると条件の不等式は、

と表せます。

こういうように、\(f(x)\)を定めて

が登場したら、ほぼ平均値の定理を使う問題とみてOK。

ここからは無理やり平均値の定理に持っていきます。

\(b-a \neq 0\)であることに注意して、全辺\(b-a\)で割ると

を示せばOKということになりますね。

平均値の定理より、

なる定数\(k\)が、\(a<k<b\)の条件で存在します。

\(f'(x)=\cos x\)なので、

条件より、\(0<a<k<b<\frac{\pi}{2}\)なので

つまり、

であることが示せましたので、題意を満たしたことになります。

平均値の定理の例題（応用）

この区間内に２点\(x_1,x_2\ (x_1< x_2)\)を取る。

関数\(f(x)\)は区間\([x_1,x_2]\)において、平均値の定理を満たす。

したがって、

を満たすような定数\(k\)が存在する。

ここで仮定より、

であり、かつ

であるから、

よって、

これは、与えられた区間内で単調増加であることを表している。

よって題意は示された。

なおこれは、

であることの証明になっています。

まとめ

楓

最後にまとめるよ。

今回は、平均値の定理が使われるのは不等式がメインというような書き方をしました。

もちろん不等式以外にも応用することは可能です。

しかし、平均値の定理の使い方をいちばん理解しやすいのは不等式。

まずは基本的な問題から取り組んでみましょう！

以上、「平均値の定理の意味と使い方」についてでした。