【陰関数】って何？って質問に全力で答えてみた【関数だけど関数じゃない】

小春

楓くん、陰関数って何？

陰関数は、これまで使ってきた関数とは一味違う表現方法のことだよ。

楓

小春

あんまり見ないけど・・・・。

陰関数は結構マイナーなところだけど、知っておかないと出題されたときに戸惑うよね。。。

楓

陰関数とは

2つの独立変数\(x,y\)をもとに

と定義されるとき、\(z\)は\(x,y\)の2変数関数といいます。

中でも、\(z=0\)、すなわち

が成り立つときを陰関数といいます。

陰関数表示

僕たちが今まで慣れ親しんだ\(y=x^2+2x-1\)のような関数を陽関数といいますが、

とおくと、\(f(x,y) = 0\)と陰関数のような形にすることができますね。

これを陰関数表示といいます。

基本的に、全ての陽関数は陰関数表示することがカンタンですが、陰関数を陽関数表示するのは困難、というより無理なことが多いです。

楓

この陰関数を陽関数表示\(y=〜\)の形にするの難しいよね・・・。

陰関数の性質

陰関数には、先ほどの

「陽関数を陰関数表示するのはラクだが、逆はむずい」

の他にも、いくつか特徴的な性質があります。

よく考えると関数ではない

と思った方、二十歳を超えたらお酒を一緒に飲みましょう笑。

例えば陰関数

を考えてみましょう。

これを陽関数表示してみると、

というように2つの関数が必要になります。

これをもとに考えると、

のように、「\(x\)を1つ決めると、\(y\)の値も1つに決まる」という関数の定義に違反していることがわかります。

マジぶっころ☆

グラフは対称的になりやすい

陰関数の微分法などを用いてグラフを描くと、ほとんどのグラフが対称的であることに気がつくと思います。

小春

これよく考えたら円の方程式だね！

楓

次元が複雑になっても、対称性があるっぽいね。

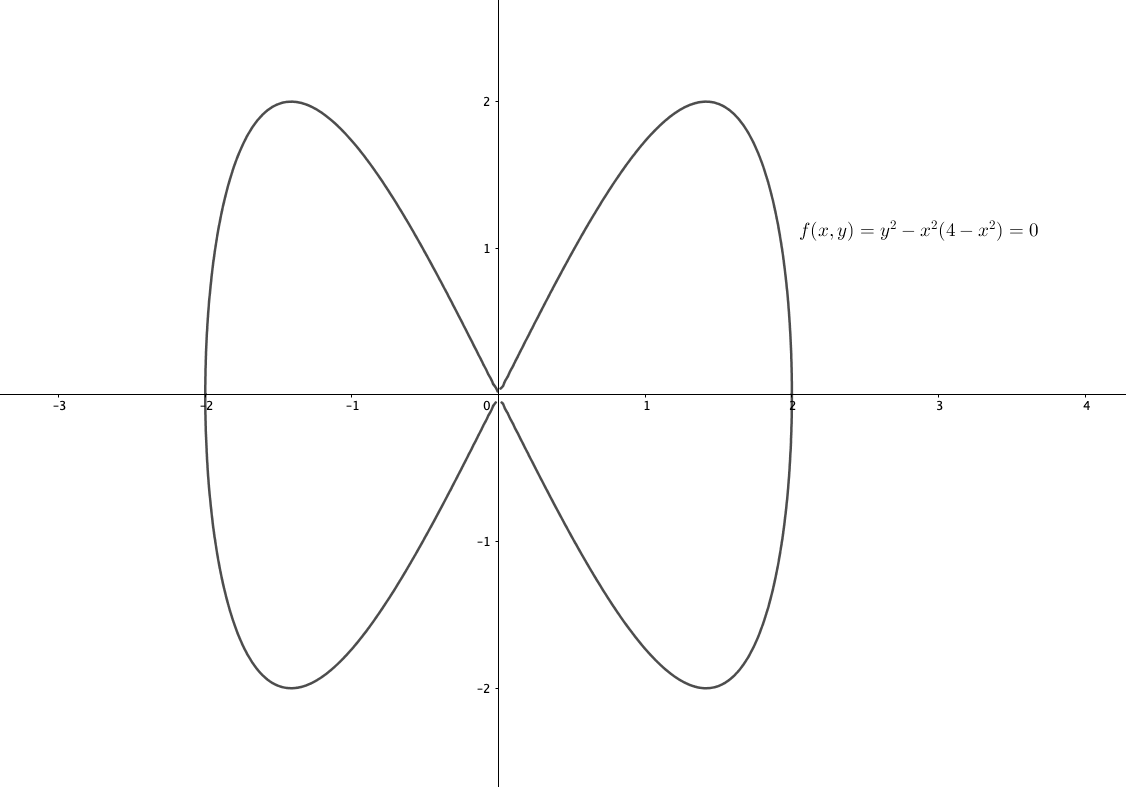
この性質は頭の片隅入れておくと、陰関数の問題を解く際に少しだけ「対称性なんじゃね？」的な感を使って、スピードアップすることができます。

なお、この「陰関数の対称性」については、別記事で詳しく説明します。

陰関数が登場する場面

陰関数のメリットを高校数学で感じるところはあまりないと思います。

大学数学では『陰関数定理』と呼ばれる、（証明が割と地獄）な定理があり、活躍の場面があるっちゃあります。

ただ陰関数は性質上、陽関数に表すのが困難でしたよね？

そのためクイズ好きな日本の入試では、本質よりも「手法知ってる〜？」みたいな感じで出題されます。

微分やグラフを描くとき、陰関数専用の手法を知っている必要がありますのでご注意ください。

まとめ

楓

今日のまとめをしますー。

入試では似たような問題を、様々な表現の仕方で出題してきます。

その中でも陰関数はぱっと見グロテスクなので、篩ふるいに掛ける意味で出題されてもおかしくありません。

陰関数には、陰関数のやり方を。

以上、「陰関数とは」についてでした。