【陰関数の微分法】カンタン3ステップ。効果的な使い方と具体例

Today's Topic

陰関数$$f(x,y)=0$$を微分するためには、両辺微分して、合成関数の微分法を使えば良い。

小春

楓く〜ん、陰関数って不気味なのに、微分法までやるの？！

あー、まぁ見た目はグロいね。でも陰関数の微分法は、一回経験しておけば大丈夫！

楓

小春

ほんと？わかりやすく教えてね！

この記事を読むと、この問題がわかる！

陰関数$$x^2+y^2-1=0$$を微分せよ。
陰関数$$f(x,y)=y^2-x^2\left(4-x^2\right)=0$$の導関数$\frac{dy}{dx}$を求めよ。

楓

例題と最後で答えを出すよ！

Contents

1 陰関数の微分法のコツ→合成関数の微分法を適用
2 陰関数の微分でやってはいけないこと
3 まとめ

陰関数の微分法のコツ→合成関数の微分法を適用

例題を通して、具体的な手法を学んでいきましょう！

楓

たったの3ステップでOK！

例題

陰関数$f(x,y) = x^2 + y^2 -1 = 0$の$x=\frac{1}{2}$における微分係数を求めよ。

STEP1. 両辺を$x$で微分

両辺を$x$について微分すると、

（左辺）
\begin{align} \frac{d}{dx}\left(x^2 + y^2 -1\right) &= 2x +\color{red}{ \frac{d}{dx}y^2} +0\\\ \end{align}

小春

$y^2$は$x$で微分できないね・・・。

STEP2. 合成関数の微分法を用いて、$\frac{d}{dx}f(y)$を解決

ここで合成関数の微分法より、

\begin{align} \color{red}{ \frac{d}{dx}y^2} &= \frac{d}{dy}y^2 \cdot \frac{dy}{dx} \\\ &= 2y\cdot \frac{dy}{dx}\\\ \end{align}

STEP3. $\frac{dy}{dx}について解く$

右辺を微分すると0。STEP2も併せて考えると、

$$2x + 2y\cdot \frac{dy}{dx} = 0$$

これを $\frac{dy}{dx}$について解くと、

$$\frac{dy}{dx} = -\frac{x}{y}$$

これで陰関数の微分はOKです。

あとは微分係数を求めるために、$x=\frac{1}{2}$を代入してあげましょう。

$x=\frac{1}{2}$のとき、$y=\pm\frac{\sqrt{3}}{2}$

よって、$x=\frac{1}{2}$のときの微分係数は

\begin{align} -\frac{x}{y} &= -\frac{\frac{1}{2}}{\pm \frac{\sqrt{3}}{2}} \cdot \frac{dy}{dx} \\\ &= \pm \frac{1}{\sqrt{3}}\\\ \end{align}

小春

繁分数の計算をすれば、あっという間に出せるね。

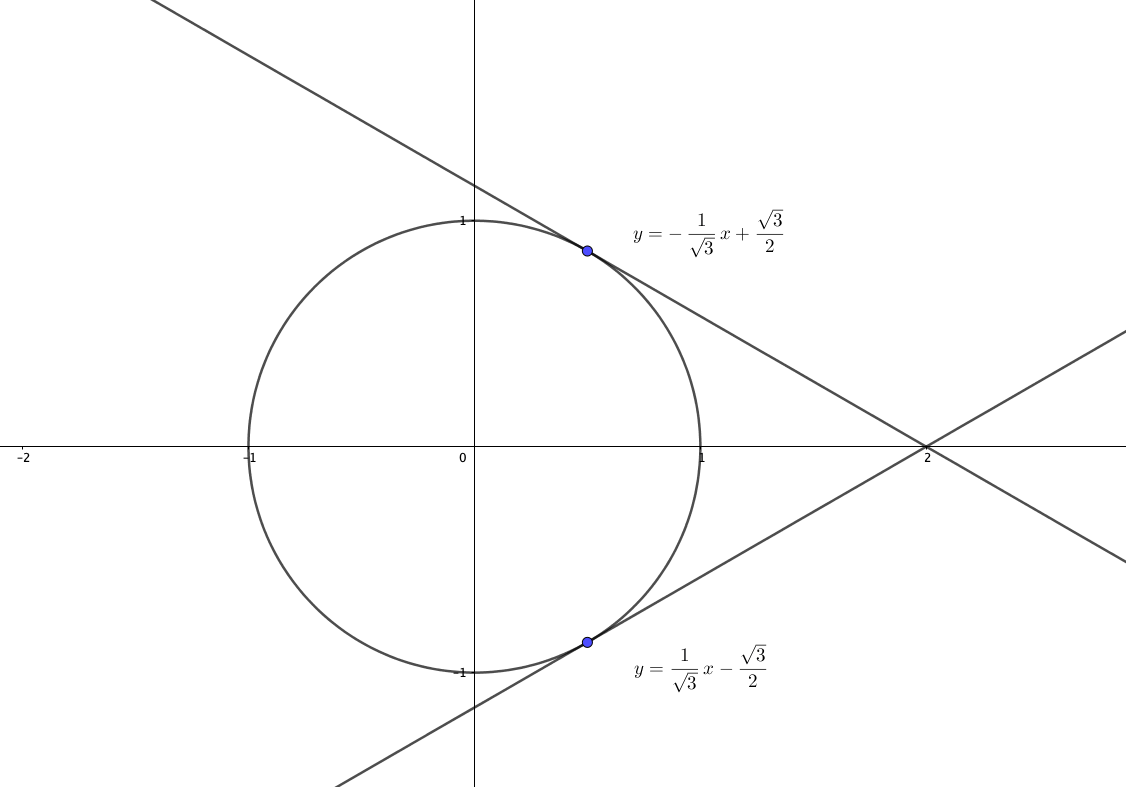
ところで、この陰関数は円の方程式を陰関数表示したものですね。

つまりこの微分係数がわかったことで、図のように$x=\frac{1}{2}$のときの円の接線の傾きがわかりました。

陰関数の微分でやってはいけないこと

陰関数の微分の問題が出題されたとき、一番やってはいけないこと。

それは陽関数表示しようと試みることです。

陰関数についての記事でも扱いましたが、基本的に陰関数は陽関数表示することが困難、というより不可能です。

先ほどの例題は確かに

$$y = \pm \sqrt{1-x^2}$$

と陽関数表示することは可能です。

では、次のような陰関数はどうでしょうか。

例題

$$f(x,y) = x^3y+x ^2 y^2 -y = 0$$

小春

いや、しんどい・・・。というかできるの・・・泣

さぁね。陽関数にしたいと思わないからどうでもいいや。

楓

合成関数の微分法をマスターしてさえいれば、今回の陰関数の微分もそれほど難しくはないですよね。

変に陽関数表示にしてから微分という、危ないしできるかもわからない手法を使うよりも、陰関数の微分法を使ったほうが安心ですね。

まとめ

楓

最後にまとめます。

まとめ

陰関数を微分するためには、

両辺を$x$で微分し、
$\frac{d}{dx}f(y)$を合成関数の微分法を使って$\frac{d}{dy}f(y)\cdot\frac{dy}{dx}$の形にし、
$\frac{dy}{dx}$について解けば良い。

数Ⅲの複雑な微分法をこれまで見てきましたが、

結局、合成関数の微分法さえできればなんとかなるんじゃね

と思ったあなた。えらい、出世します。

陰関数の問題自体は頻出するわけではありませんが、おまけ程度に頭の片隅に入れておきたいですね。

以上、「陰関数の微分法について」でした。

チェック問題

例題

陰関数$$f(x,y)=y^2-x^2\left(4-x^2\right)=0$$の導関数$\frac{dy}{dx}$を求めよ。

両辺$x$について微分すると、

（左辺）

\begin{align} \frac{d}{dx}y^2-\frac{d}{dx}\left\{x^2(4-x^2)\right\} &= \underbrace{\frac{d}{dy}y^2\cdot\frac{dy}{dx}}_{合成関数の微分法} - \underbrace{2x(4-x^2)-2x^3}_{積の微分法}\\\ &= 2y\cdot\frac{dy}{dx}+4x(x^2-2)\\\ \end{align}

（※見切れている場合はスクロール）

（右辺）は0なので、

$$2y\cdot\frac{dy}{dx}+4x(x^2-2) = 0$$

$y\neq 0$として$\frac{dy}{dx}$について解くと、

$$\frac{dy}{dx} = -\frac{2x(x^2-2)}{y}$$

ちなみに陰関数$f(x,y)=0$を陽関数表示してみると、

$$y = x\sqrt{4-x^2}$$

となるので、

$$\frac{dy}{dx} = -\frac{2x(x^2-2)}{ x\sqrt{4-x^2}}$$

と表すこともできます。

楓

ただし、$x\neq 0,\pm 2$であることに注意！

【陰関数の微分法】カンタン3ステップ。効果的な使い方と具体例

陰関数の微分法のコツ→合成関数の微分法を適用

STEP1. 両辺を\(x\)で微分

STEP2. 合成関数の微分法を用いて、\(\frac{d}{dx}f(y)\)を解決

STEP3. \(\frac{dy}{dx}について解く\)

陰関数の微分でやってはいけないこと

まとめ

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則