今回の例題
\(x^3-3x^2-9x-m=0\)が異なる3つの実数解を持つとき、定数\(m\)の値の範囲を求めよ。
【難易度:】
3次方程式のグラフの形を考えて、極値や\(x\)軸に着目する。


解答
\(f(x)=x^3-3x^2-9x-m\)とする。
\(f'(x)=0\)のとき、\(x=-3,1\)。
よって増減表は次のようになる。
| $$x$$ | $$\cdots$$ | $$-1$$ | $$\cdots$$ | $$3$$ | $$\cdots$$ |
| $$f'(x)$$ | $$+$$ | $$0$$ | $$-$$ | $$0$$ | $$+$$ |
| $$f(x)$$ | $$\nearrow$$ | $$f(-1)$$ | $$\searrow$$ | $$f(3)$$ | $$\nearrow$$ |
つまり\(y=f(x)\)のグラフは以下のようになる。
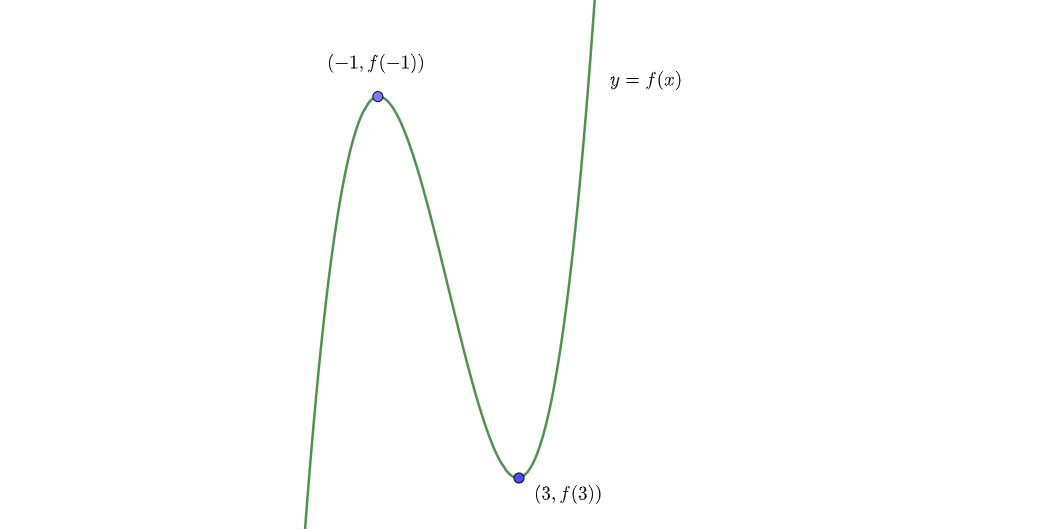
ここで、\(f(x)\)が3つの異なる実数解を持つとき、\(y=f(x)\)は\(x\)軸(\(y=0\))と次のように交われば良い。
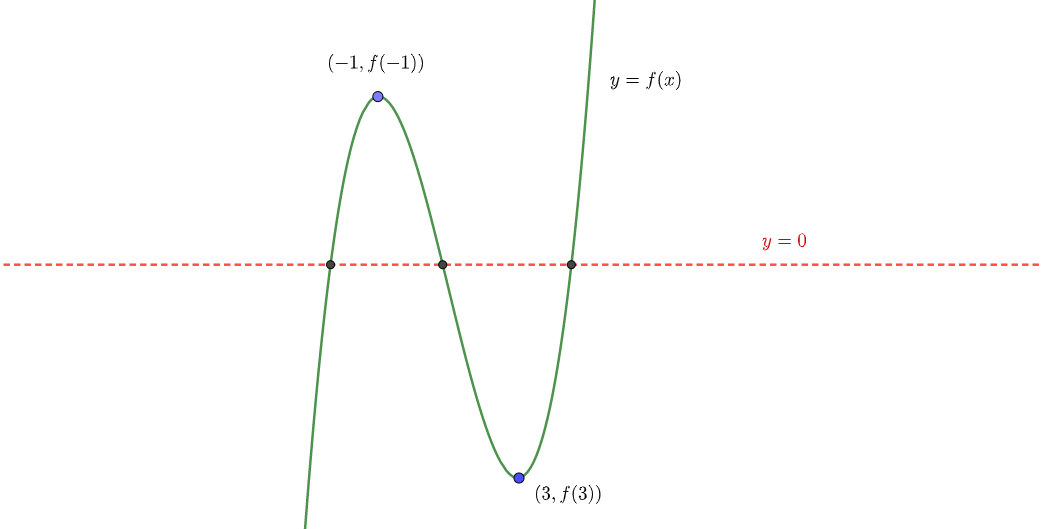
よって、次の条件が成り立てば良い。
極大値と極小値に着目すると、
$$(極大値)\times(極小値)<0$$
であれば良い。
よって、
(※見切れている場合はスクロール)
これを満たすのは、
$$\left\{ \begin{array}{l} 5-m<0かつm+27<0 \cdots ①\\ 5-m>0かつm+27>0 \cdots② \end{array} \right. $$
①は\(5<m<-27\)より不適
②より\(-27<m<5\)
解答のポイント
似たような問題は、どのように解けばいいのでしょうか。
ここからは、問題を解く上での観点を紹介します。
解答の流れ
方程式\(f(x)=0\)の解\(x\)は、\(y=f(x)\)と\(y=0\)、つまり\(x\)軸との交点の\(x\)座標を表していることに着目します。
すると、
- 実数解の個数が3つ→\(x\)軸との交点が3つである
- 実数解の個数が2つ→\(x\)軸との交点が2つである
- 実数解の個数が1つ→\(x\)軸との交点が1つである
- 実数解の個数が0→\(x\)軸との交点がない
ということが言えますね。
三次関数の場合▼
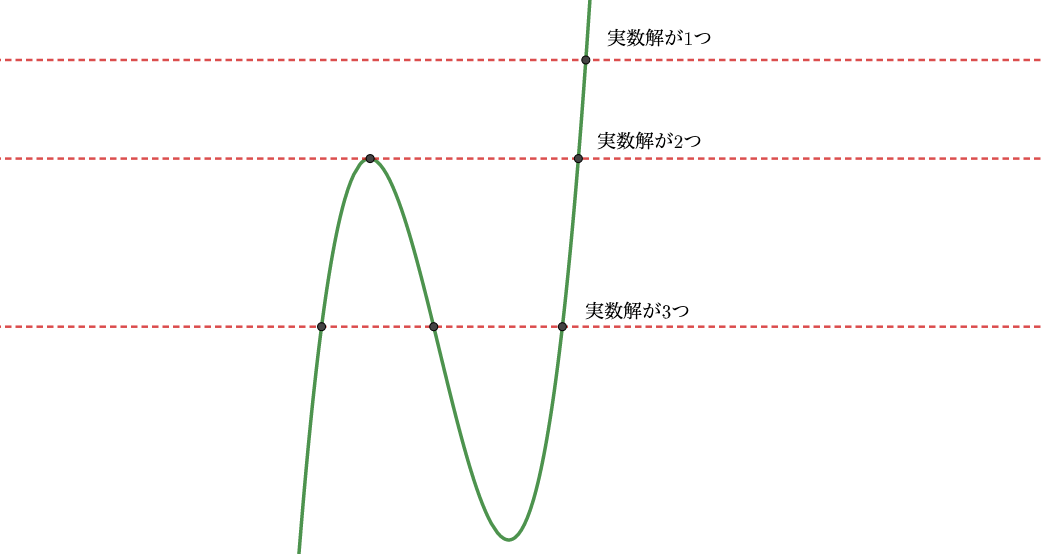
また三次関数のグラフの形にも注目してみると、
- 極小値<\(x\)軸<極大値 →実数解3つ
- 極小値=\(x\)軸、極大値=\(x\)軸 →実数解2つ
- \(x\)軸<極小値、極大値<\(x\)軸 →実数解1つ
と言えることがわかります。
よって実数解の個数を判断する条件として、極値と\(x\)軸の関係を調べればOK。
位置に着目するか、符号に着目するか
解答では2つの方法を示しました。
解法①では極大値が\(x\)軸よりも大きいこと、極小値が\(x\)軸よりも小さいことを利用しています。
また、このとき極大値\(\times\)極小値は必ず負になることがわかります。
これを利用しているのが解法②。


結局どちらも同じことを言っているので、計算量などでお好きな方を選んでください。
まとめ
まとめ
方程式\(f(x)=0\)の実数解の個数を調べるためには、
- \(y=f(x)\)のグラフを考えて、
- \(x\)軸との交点を調べれば良い。
極値がある場合には、極大値や極小値に着目すれば良い。


以上、「実数解の個数問題」でした。
練習
問題
\(x^3-3a^2x+4a=0\)が異なる3つの実数解を持つとき、定数\(a\)の値の範囲を求めよ。
\(f(x)=x^3-3a^2x+4a\)とすると、
メモ
ここで\(a\)の値によって、極大値・極小値の個数が変わることに注意してください。
(ⅰ)\(a=0\)のとき、
\(x=0\)で\(f'(x)=0\)となるが、その前後で符号が変わらないため単調増加。
つまり実数解は1つしか存在しない。
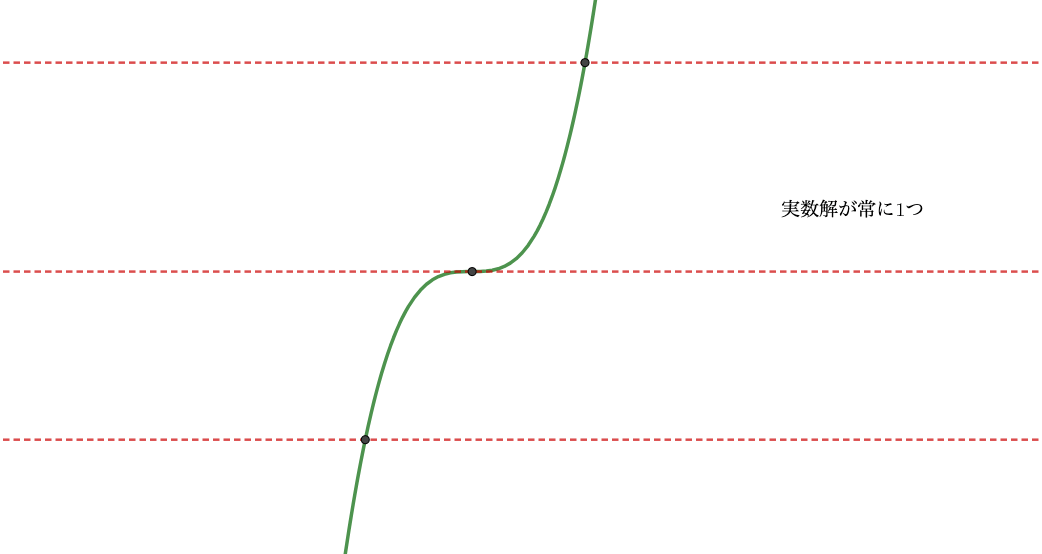
(ⅱ)\(a\neq 0\)のとき、
\(x=\pm a\)のとき極値をとる。
\(a\)の符号によって極大値、極小値の値は変わるが、
は必ず満たす。
よって、
(※見切れている場合はスクロール)
これにより\(a^2-2>0\)。











