【グラフの曲がり方】『グラフを描け』を最速で解くための最強スキルを公開。

Today's Topic

2点を結ぶグラフの曲がり方には、

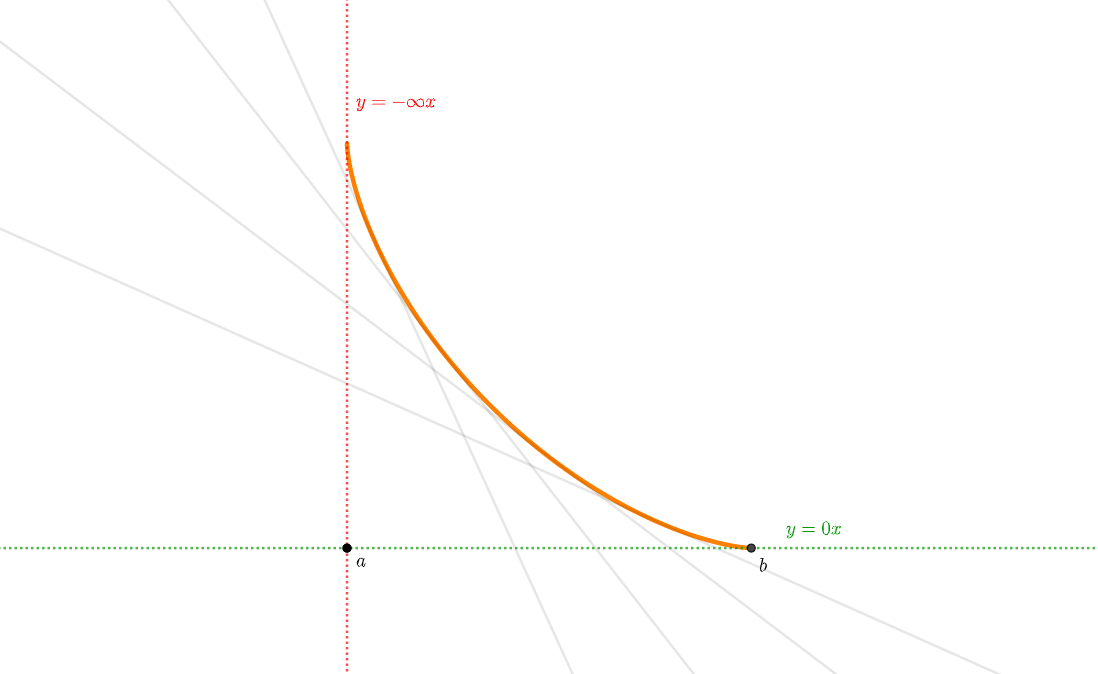
【$\infty ＆ 0$型】
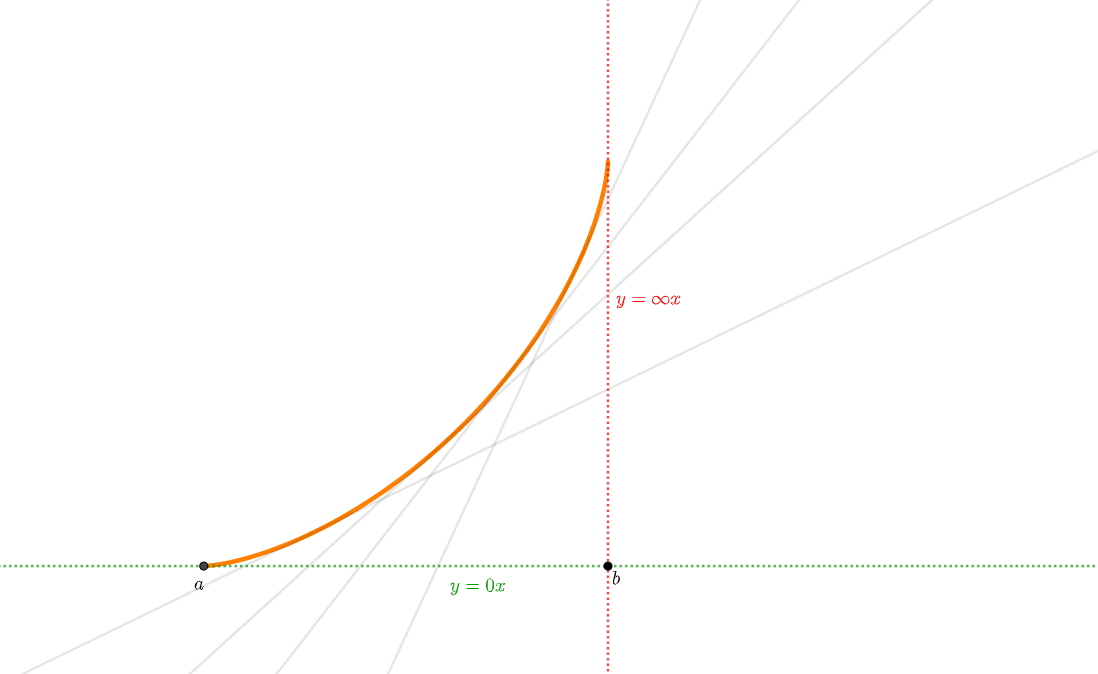
【$0 ＆ \infty$型】
【$-\infty ＆ 0$型】
【$0 ＆ -\infty$型】

の4通りがある。

楓

さて、今日はグラフの曲がり方について考えていこう！

曲がり方？増減表のときに扱ったカーブのこと？

小春

楓

そう！その最後に増減表の弱点について話したね。今日はその弱点を補う考え方を紹介するよ！

ということは今後、数Ⅲとかでも大事になりそうね。

小春

この記事を読むと、この意味がわかる！

変曲点を調べる意味
グラフの曲がり方を正確に、かつ簡単に知るテクニック

Contents

1 1階微分の弱点
2 グラフの曲がり方は4パターン
3 曲がり方を調べる2通りの方法
4 まとめ

1階微分の弱点

数Ⅱで学んだ増減表では、カーブする地点で接線の傾きの正負が切り替わることに着目して、グラフのおおよその形を把握することができました。

しかしこの方法には、1つだけとんでもない弱点があるのです。

それは与えられた方程式が未知の場合は、使い物にならないということです。

増減表を元に書いたグラフはこれまで3次関数や4次関数程度ではないでしょうか。

これらはあらかじめグラフの形がわかっているので、増減表を見ておおよそこの形になるだろうと推察すいさつできます。

$$x$$	$$\cdots$$	$$a$$	$$\cdots$$	$$b$$	$$\cdots$$
$$y'$$	$$+$$	$$0$$	$$-$$	$$0$$	$$+$$
$$y$$	$$\nearrow$$	$$f(a)$$	$$\searrow$$	$$f(b)$$	$$\nearrow$$

三次関数であるという前提があれば・・・

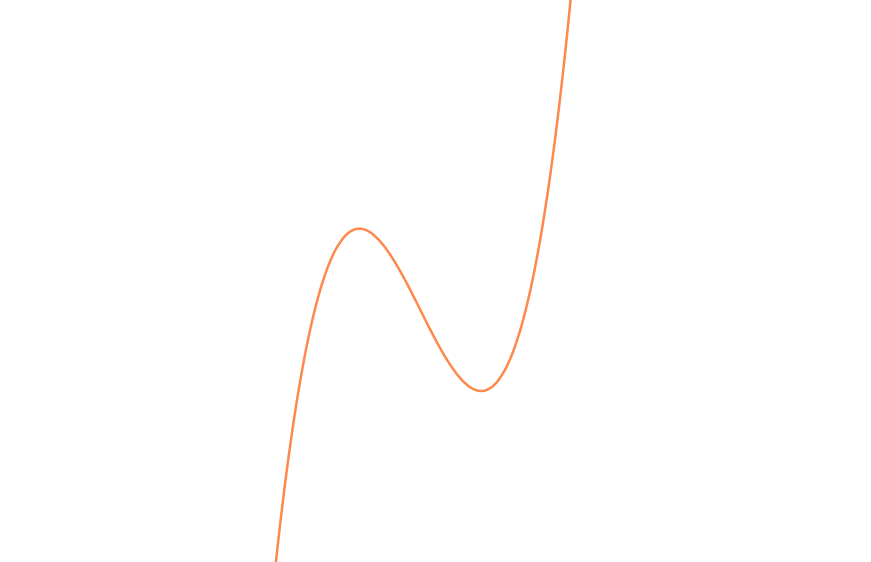
ですが未知の方程式の場合、同じ増減表ができても、カーブの仕方によって様々なグラフが考えられます。

例

小春

確かに増減表と一致しているね・・・。

つまり増減表を書いても、どんなグラフになるかわからないというわけ。

楓

グラフの曲がり方は4パターン

そこでまず重要になるのが、一体グラフの曲がり方は何パターンあるのか、です。

結論から言うと4パターン。

それぞれの特徴を見ていきましょう。

楓

ちなみに名前は僕が勝手につけたやつだよ笑

【値の増加を表すカーブ】

【$\infty ＆ 0$型】

接線の傾きは常に正の値を取り、次第に0に近づくように緩やかになる。

$$f’(x)\underset{x \to a}{\longrightarrow} \infty $$

$$f’(x)\underset{x\to b}{\longrightarrow} 0 $$

【$0 ＆ \infty$型】

接線の傾きが0をスタートして、どんどん大きくなる。

$$f’(x)\underset{x \to a}{\longrightarrow} 0 $$

$$f’(x)\underset{x\to b}{\longrightarrow} \infty $$

【値の減少を表すカーブ】

【$-\infty ＆ 0$型】

接線の傾きは常に負の値を取り、それがだんだんと0に近づくように緩やかになる。

$$f’(x)\underset{x \to a}{\longrightarrow} \infty $$

$$f’(x)\underset{x\to b}{\longrightarrow} 0 $$

【$0 ＆ -\infty$型】

接線の傾きが0をスタートして、どんどん小さく、つまり負の方向に大きくなる。

$$f’(x)\underset{x \to a}{\longrightarrow} 0 $$

$$f’(x)\underset{x\to b}{\longrightarrow} -\infty $$

曲がり方を調べる2通りの方法

それでは未知の方程式だけ与えられた場合、2点を結ぶ曲線が上記4パターンのどれに該当するのか調べる方法をご紹介します。

結論から言うと、2階微分するか極限を調べるかの２タイプしかありません。

2階微分を調べる

あるグラフに対して、微分した値、つまり導関数は接線の傾きを表していました。

では2階微分は何を表すのでしょうか。

簡単に言ってしまえば接線の傾きの未来を表します。

2階微分の値が

正であれば、接線の傾きが増加傾向
負であれば、接線の傾きが減少傾向

ということになります。

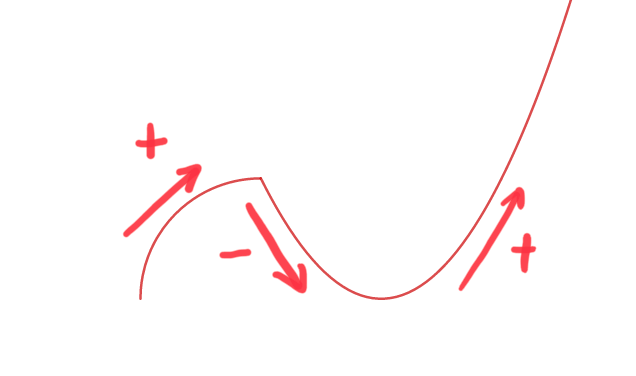
例えば2階微分の値が正であるとき、曲がり方は次の2つに絞られます。

小春

確かに接線の傾きが、どちらも増加しているね。

ここでさらに1階微分の値が正であれば

グラフは増加傾向にあり、かつ接線の傾きは増加傾向

なので、こちらに絞られます。

一覧で簡単に示すと、このような感じです。

カーブの仕方一覧

1階微分の符号	$$+$$	$$-$$	$$+$$	$$-$$
2階微分の符号	$$-$$	$$+$$	$$+$$	$$-$$
グラフのカーブの仕方

楓

この表は暗記するのではなく、「なぜそのカーブを表すのか」をしっかりと理解しておこう！

例題

1階微分の値が正、2階微分の値が負のときはどのような曲がり方をするでしょうか。

2階微分の値が負のとき、考えうる曲がり方は次の2通り。

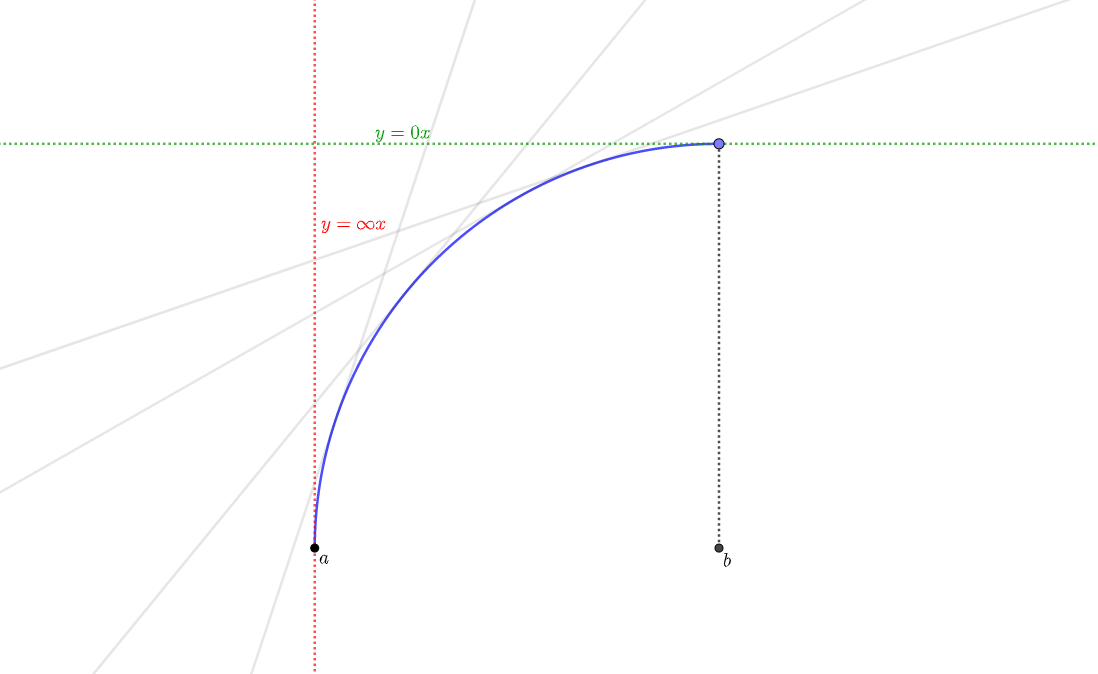
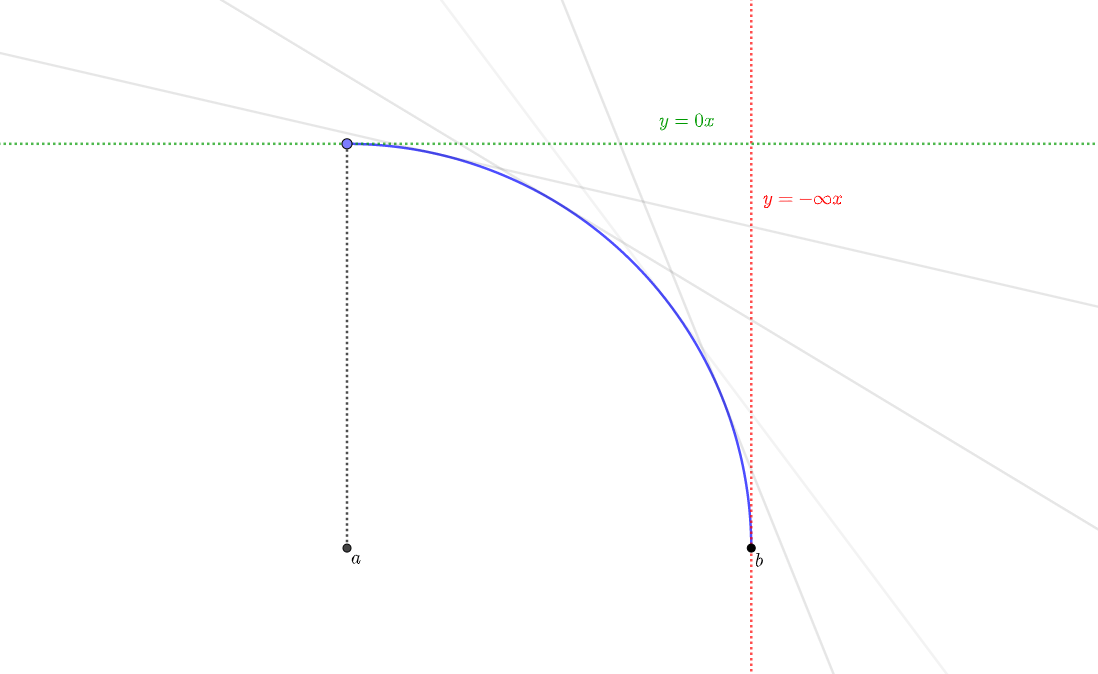
1階微分が正なので、

グラフは増加傾向にあり、かつ接線の傾きは減少傾向

なので、この曲がり方で確定です。

極限を調べる

先ほど曲がり方4つの型を紹介しました。

そのときに接線の傾き$f’(x)$が端点$a$や$b$に近づくとき、どのような極限値になるのかを同時に記載しましたね。

要はこの極限を調べれば、曲がり方はわかります。

具体的な問題で見てみましょう。

例題

$y=\tan x$のグラフを$-\frac{\pi}{2}≦x≦\frac{\pi}{2}$の範囲で描け。ただし$y'=\frac{1}{\cos^2 x}$は認めて良い。

$$\left. \begin{array}{l} y' \underset{x\to -\frac{\pi}{2}}{\longrightarrow} \infty \\ y' \underset{x\to -0}{\longrightarrow} 1 \end{array} \right\} 【\infty ＆ 1】$$
$$\left. \begin{array}{l} y' \underset{x\to +0}{\longrightarrow} 1 \\ y' \underset{x\to \frac{\pi}{2}}{\longrightarrow} \infty \end{array} \right\} 【1 ＆ \infty】$$

小春

必ずしも$0$か$\infty$なわけではないんだね。

そう、ごくたまに$y=x$のような具体的な接線に近づくことがあるよ。

楓

よって、次のようなことがわかる。

$y=\tan x$のグラフは$x=0$に近づくほど接線の傾きが1に近づき、

$-\frac{\pi}{2}$に向かうほど、接線の傾きが大きくなる
$\frac{\pi}{2}$に向かうほど、接線の傾きが大きくなる

よってグラフは次のようになる。

小春

ほんとだ！原点付近はほぼ$y=x$と重なるね！

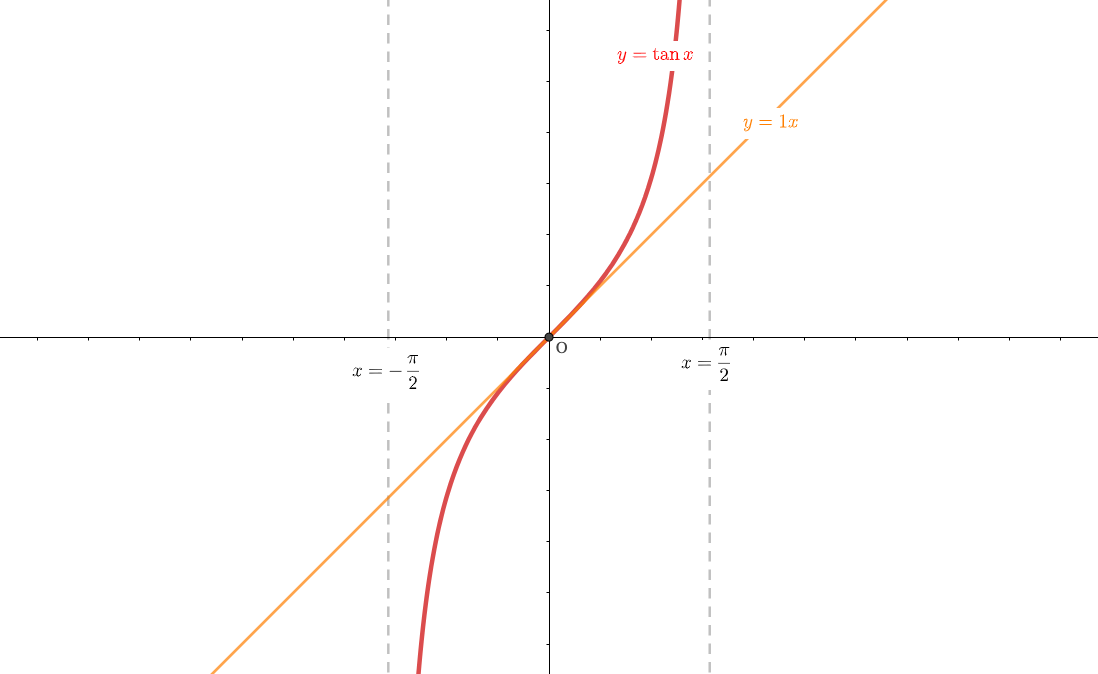
2つの手法の使い分けかた

この2つの手法には、それぞれ適した場面があります。

【2階微分を使う手法】

変曲点のあるグラフを描く
極限を求めようにも複雑で、微分したほうが早い

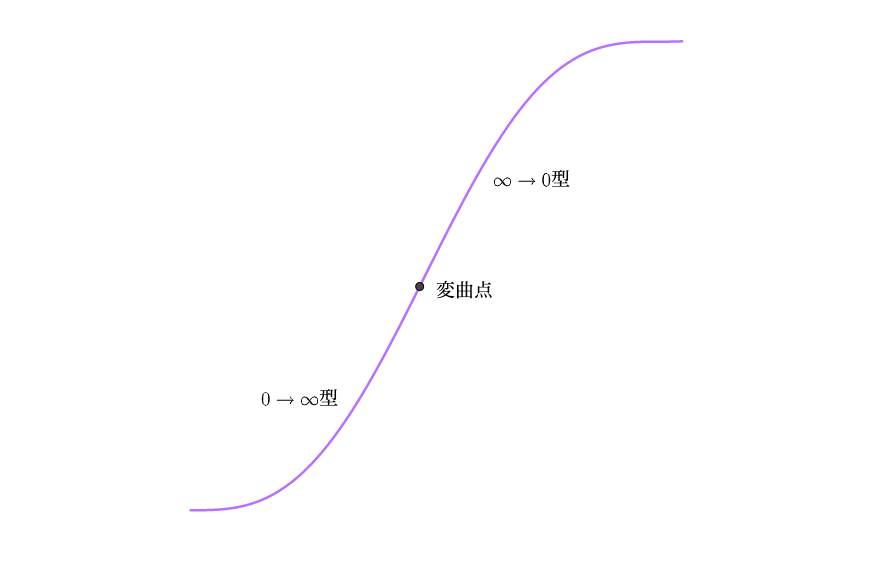
特に、変曲点と呼ばれる曲がり方が突然変わる点は、2階微分の方が求めやすいということを押さえましょう。

楓

極限を使う方法だと、この変曲点の存在に気づけないんだよね。

: 【増減、凹凸を調べ、グラフを描け】意味を考えれば、凹凸グラフは迷わず解けるよ。

続きを見る

【極限を使う手法】

極限の計算の方が、2階微分より手間でない
媒介変数表示のグラフを描く

特に媒介変数表示で表されたグラフは、この極限を使う手法の方が圧倒的に早く、簡単です。

2階微分を使ってできないことはないですが、恐ろしくめんどくさい微分をする必要があります。

楓

「できること」と、「していいこと」は別！効率的な手法を選びましょう！

: 【媒介変数表示のグラフ】2階微分は絶対するな！極限を使った超カンタン解答方法

続きを見る

まとめ

楓

最後にまとめをしましょう。

まとめ

2点を結ぶグラフの曲がり方には、

【$\infty ＆ 0$型】
【$0 ＆ \infty$型】
【$-\infty ＆ 0$型】
【$0 ＆ -\infty$型】

の4通りがあるが、ごくまれに具体的な接線の傾きに近づく。

変曲点を求めるためには、2階微分を用いれば良い。

媒介変数表示のグラフを描くためには、極限を用いれば良い。

今回はグラフの曲がり方という、みんな知らないけど超重要な観点についてお話ししました。

この感覚が身についていると、「グラフを描け」問題はマジで簡単になります。

公式暗記や小手先だけのテクニックではなく、本当の意味をしっかり理解しておきましょう。

以上、「グラフの曲がり方」についてでした。

【グラフの曲がり方】『グラフを描け』を最速で解くための最強スキルを公開。

1階微分の弱点

グラフの曲がり方は4パターン

曲がり方を調べる2通りの方法

2階微分を調べる

極限を調べる

2つの手法の使い分けかた

【2階微分を使う手法】

【増減、凹凸を調べ、グラフを描け】意味を考えれば、凹凸グラフは迷わず解けるよ。

【極限を使う手法】

【媒介変数表示のグラフ】2階微分は絶対するな！極限を使った超カンタン解答方法

まとめ

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則