【媒介変数表示されたグラフの接線】を、たったの3ステップで求めよう！

Today's Topic

$$y-y(t) = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}\left(x-x(t)\right)$$

楓

今日は媒介変数のグラフの接線を求めるよ！

媒介変数の微分法があったから、そんな感じはしたよ...

小春

楓

でも大丈夫、今まで通りのステップをこなすだけでOKだから！

この記事を読むと、この意味がわかる！

$$\left\{ \begin{array}{l} x= \cos^3\theta \\ y = \sin^3 \theta \end{array} \right. $$
の$\theta = \frac{\pi}{3}$における接線の方程式と、その時の接点を求めよ。
$$\left\{ \begin{array}{l} x= t- \sin t \\ y = 1-\cos t \end{array} \right. $$
の$t = \frac{\pi}{4}$における接線の方程式を求めよ。

楓

例題と最後の問題で扱うよ！

Contents

1 媒介変数表示されたグラフでも、接線を求める手順は一緒
2 まとめ

媒介変数表示されたグラフでも、接線を求める手順は一緒

接線の方程式を求めるテクニックについての記事でも紹介した、たった3つのステップを行えばOKです。

ここでは例として、次の問題を解いてみましょう。

例題

$$\left\{ \begin{array}{l} x= \cos^3\theta \\ y = \sin^3 \theta \end{array} \right. $$

の$\theta = \frac{\pi}{3}$における接線の方程式と、その時の接点を求めよ。

では順番に行なっていきますね。

STEP1　導関数$\frac{dy}{dx}$を求める。

媒介変数表示されているグラフの場合、媒介変数の微分法を利用して導関数を求めましょう。

$x,y$それぞれを、$\theta$で微分すると、

$$f(x)=\left\{ \begin{array}{l} \frac{dx}{d\theta} = -3\cos^2\theta\sin\theta \\ \frac{dy}{d\theta} = 3\sin^2\theta\cos\theta \end{array} \right. $$

楓

ここでは合成関数の微分法を使ったよ！

よって、媒介変数の微分法より

\begin{align} \frac{dy}{dx} &= \frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}\\\ &= \frac{3\sin^2\theta\cos\theta}{-3\cos^2\theta\sin\theta} \\\ &= -\tan \theta\\\ \end{align}

のように、目的の導関数$\frac{dy}{dx}$が手に入りました！

STEP2　接点を求めて、微分係数を導出

今回は$\theta = \frac{\pi}{3}$における接線なので、接点は

$$f(x)=\left\{ \begin{array}{l} x= \left(\cos \frac{\pi}{3}\right)^3 \\ y= \left(\sin \frac{\pi}{3}\right)^3 \end{array} \right. $$

より、$\left(\frac{1}{8}, \frac{3}{8}\sqrt{3}\right)$となりますね。

導関数$\frac{dy}{dx}$は$\theta$の関数なので、$\theta = \frac{\pi}{3}$を代入すると、

\begin{align} \frac{dy}{dx} &= -\tan \frac{\pi}{3}\\\ &= -\sqrt{3} \end{align}

小春

つまり接点$\left(\frac{1}{8}, \frac{3}{8}\sqrt{3}\right)$における接線の傾きは、$-\sqrt{3}$ということだね！

STEP3 傾き$\frac{dy}{dx}$の直線を、接点を通るように平行移動

最後は接線と平行な直線$y= \frac{dy}{dx} x$が、接点を通るように平行移動してあげれば終了です。

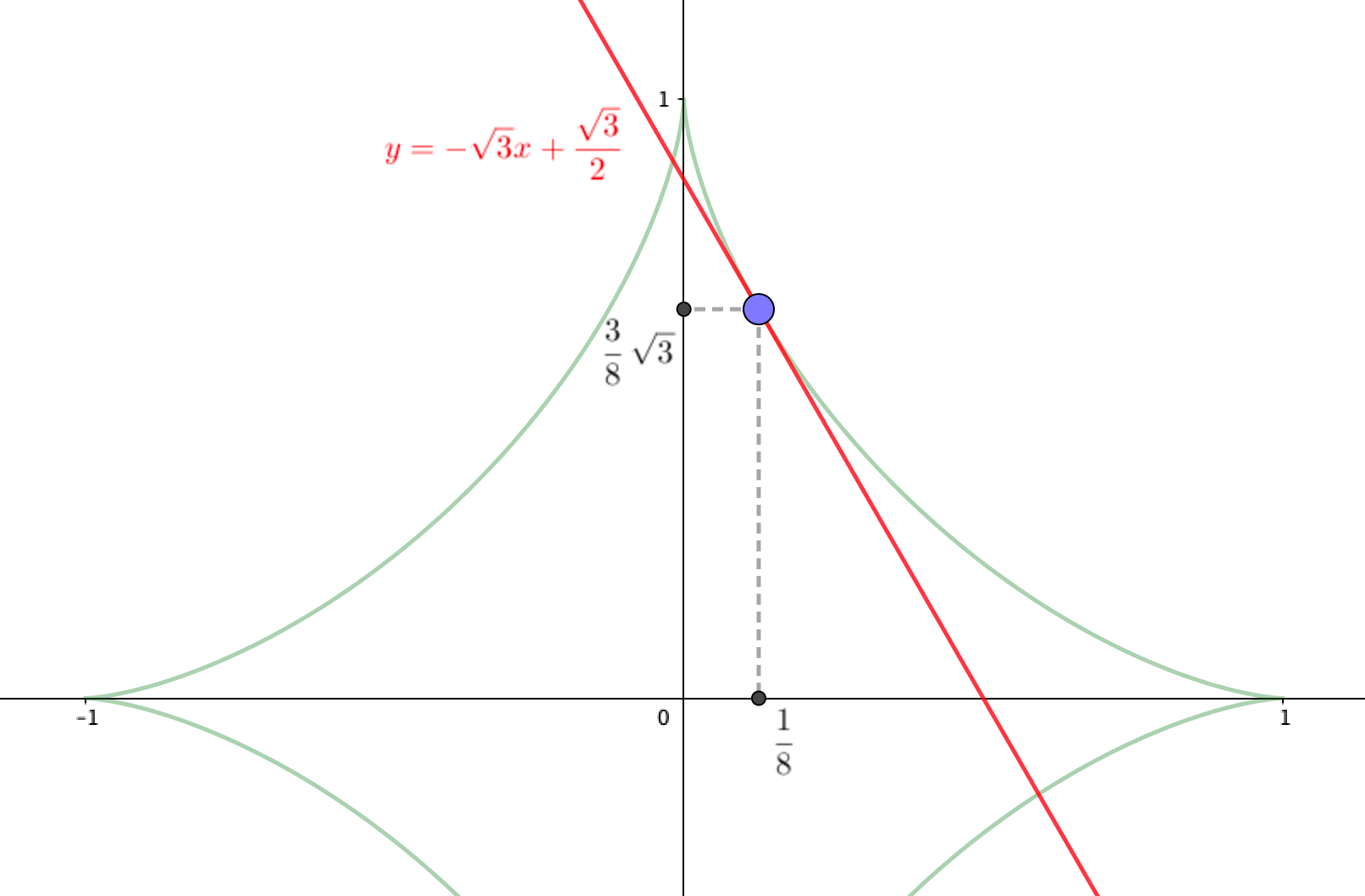
$y=-\sqrt{3}x$を、点$\left(\frac{1}{8}, \frac{3}{8}\sqrt{3}\right)$を通るように平行移動させると、

$$y - \frac{3}{8}\sqrt{3} = -\sqrt{3}\left(x-\frac{1}{8}\right)$$

以上より、答えは

接線：$y = -\sqrt{3}x + \frac{\sqrt{3}}{2}$
接点：$\left(\frac{1}{8}, \frac{3}{8}\sqrt{3}\right)$

となります。

ちなみに、実際に図を描いてみるとこんな感じ。

小春

ほ、本当に接線の方程式なんだぁー！

まとめ

今回は媒介変数表示されたグラフの接線を求めるテクニックをご紹介しました。

と言っても手順は、以前紹介した接線の方程式を求めるテクニックとほとんど変わりません。

楓

やっぱりこの方法が一番ラクなんだよね。

媒介変数表示の微分法も難しくないので、ここら辺は苦手意識を持たずにちゃちゃっとマスターしてしまいましょう！

以上、「媒介変数表示されたグラフの接線の方程式の求め方」についてでした。

チェック問題

例題

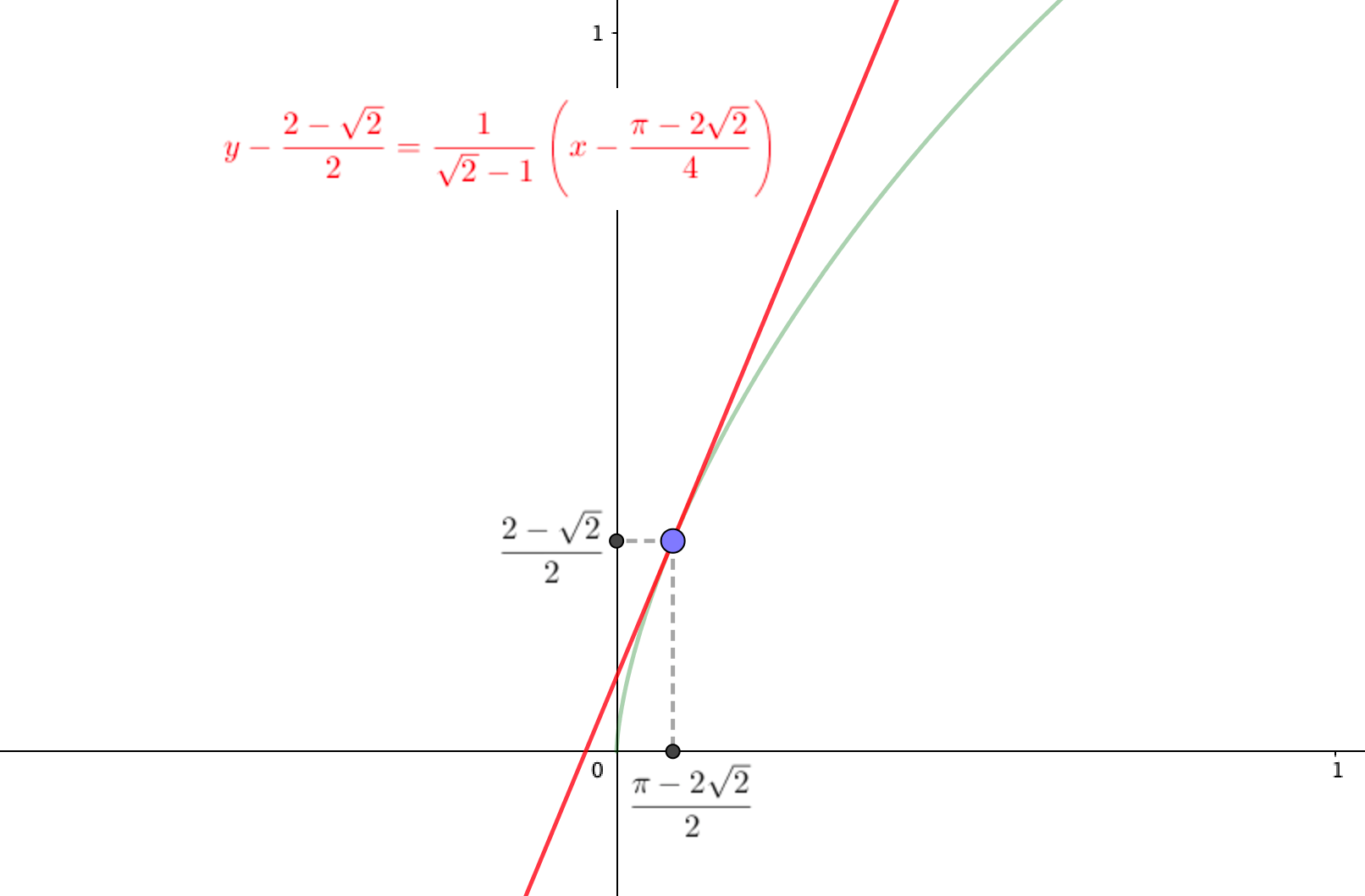
$$\left\{ \begin{array}{l} x= t- \sin t \\ y = 1-\cos t \end{array} \right. $$

の$t = \frac{\pi}{4}$における接線の方程式を求めよ。

$\frac{dx}{dt} = 1-\cos t ,\ \frac{dy}{dt} = \sin t$より、

\begin{align} \frac{dy}{dx} &= \frac{\frac{dy}{dt}}{\frac{dx}{dt}}\\\ &= \frac{\sin t}{1-\cos t}\\\ \end{align}

よって$t=\frac{\pi}{4}$のとき、接線の傾きは

\begin{align} \frac{\sin \frac{\pi}{4}}{1-\cos\frac{\pi}{4} } &= \frac{\frac{1}{\sqrt{2}}}{1-\frac{1}{\sqrt{2}}}\\\ &= \frac{1}{\sqrt{2}-1}\\\ \end{align}

小春

繁分数で計算すればラクだね！

また接点は$t=\frac{\pi}{4}$のとき、

$$\left\{ \begin{array}{l} x=\frac{\pi}{4} -\sin \frac{\pi}{4} = \frac{\pi - 2\sqrt{2}}{4} \\ y=1-\cos \frac{\pi}{4} =\frac{2-\sqrt{2}}{2} \end{array} \right. $$

以上より、直線$y=\frac{1}{\sqrt{2}-1} x$が点$\left(\frac{\pi - 2\sqrt{2}}{4}, \frac{2-\sqrt{2}}{2} \right)$を通るとき接線となるので、求める接線の方程式は

$$y - \frac{2-\sqrt{2}}{2} = \frac{1}{\sqrt{2}-1} \left(x-\frac{\pi - 2\sqrt{2}}{4}\right)$$